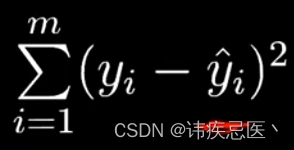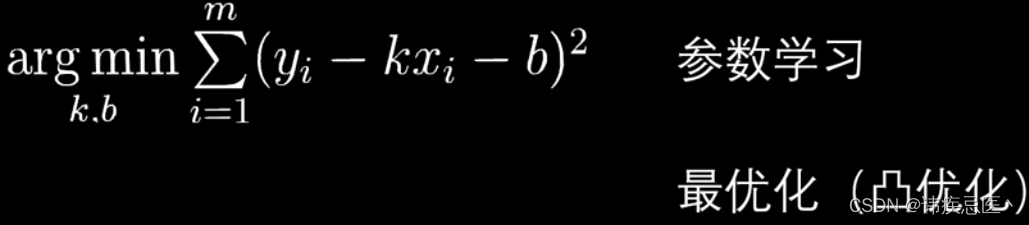线性、逻辑回归算法学习

news2025/1/2 0:09:11

1、什么是一元线性回归

线性：两个变量之间的关系是一次函数，也是数据与数据之间的关系。
回归：人们在测试事物的时候因为客观条件所限，求的都是测试值，而不是真实值，为了无限接近真实值，无限次的进行测量，最后通过这些测量数据计算回归到真实值，这就是回归的由来。
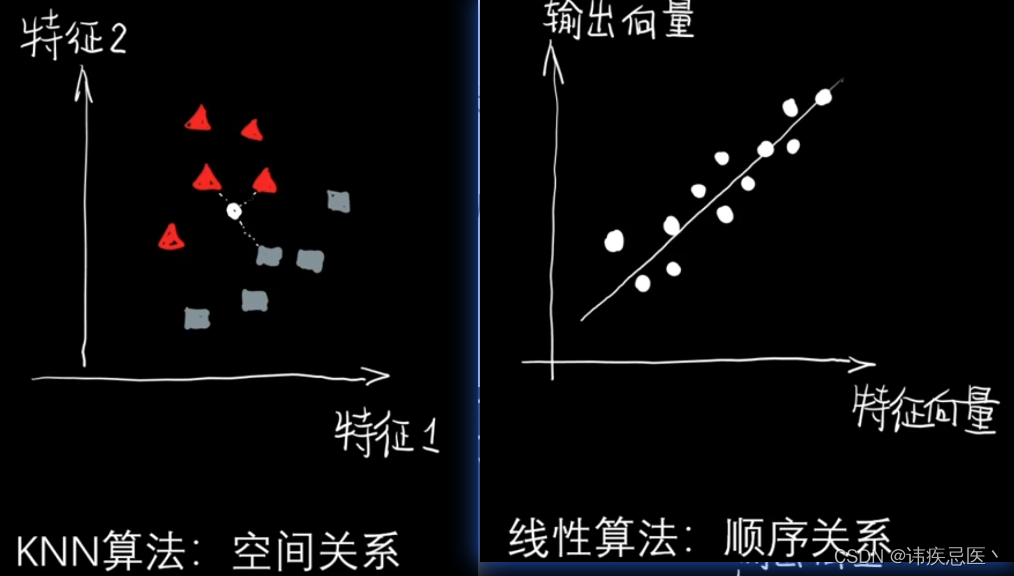
KNN最近邻值是：KNN横纵轴坐标为两个特征，比如身高体重与某种疾病关系。
一元线性回归：只有横轴是特征，纵轴是输出值，比如股价与时间的关系。
通俗的说就是用一个函数去逼近这个真实值

在这里插入图片描述

1.2、线性回归解决什么问题

通过大量样本数据进行处理，可以得出一个 比较符合事物内部规律的y=kx+b，从而对结果进行预测，解决的就是通过已知样本数据，预测未知数据，比如房价进行预测，电影票房预测。

计算k和b的计算公式：
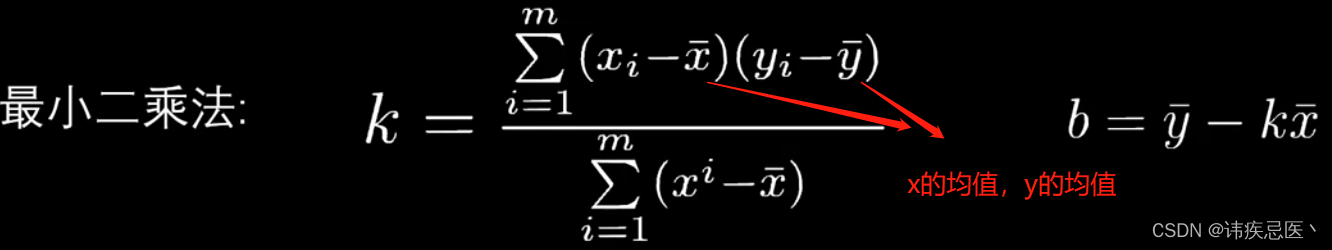
在这里插入图片描述

损失函数(loss function)，衡量了误差大小，不断地去优化，找出最优解，平方残差和是最常用的一种方式
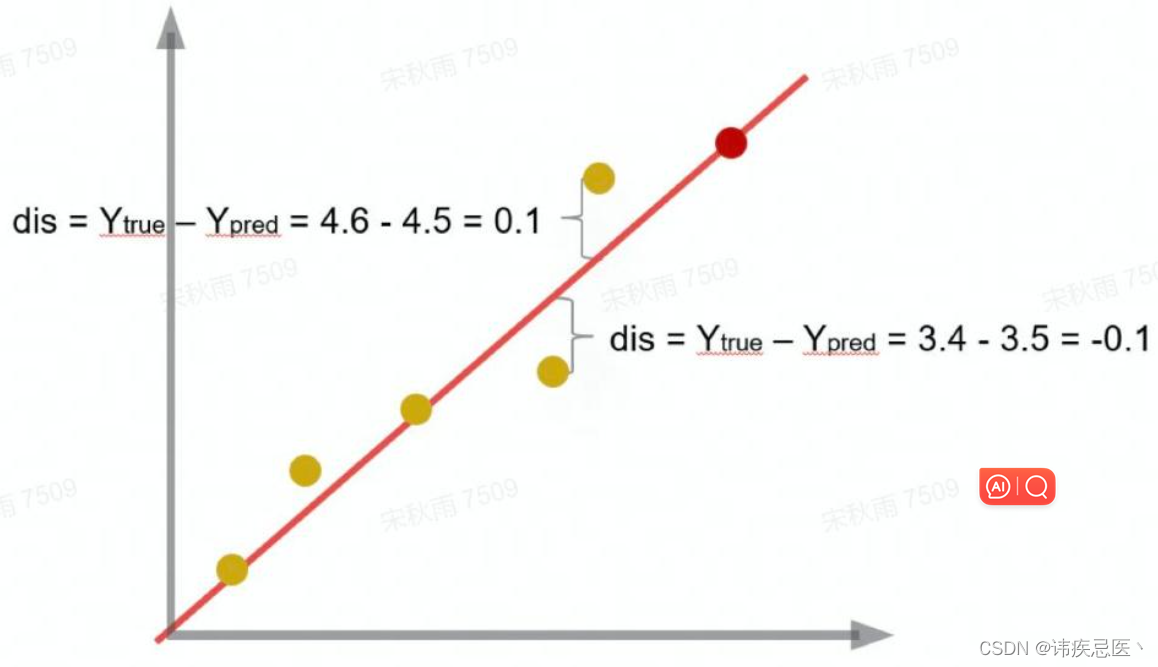
在这里插入图片描述在这里插入图片描述

在这里插入图片描述

1.3、实现一元线性回归

在这里插入图片描述

# 使用boston数据集 
import numpy as np
import matplotlib.pyplot as plt
import sklearn
from sklearn.model_selection import train_test_split
import pandas as pd 

# 加载波士顿房屋数据集
data_url = "http://lib.stat.cmu.edu/datasets/boston"
raw_df = pd.read_csv(data_url, sep="\s+", skiprows=22, header=None)
data = np.hstack([raw_df.values[::2, :], raw_df.values[1::2, :2]])
target = raw_df.values[1::2, 2]

from sklearn.model_selection import train_test_split
# 拆分数据集
x_train,x_test,y_train,y_test = train_test_split(data,target,train_size=0.7,random_state=233)

x_train[:,5].shape,y_train.shape
plt.scatter(x_train[:,5],y_train)

def fit(x,y):
    a_up = np.sum((x-np.mean(x))*(y-np.mean(y)))
    a_bottom = np.sum((x-np.mean(x))**2)
    a = a_up/a_bottom
    b = np.mean(y) - a *np.mean(x)
    return a,b

a,b = fit(x_train[:,5],y_train)
a,b

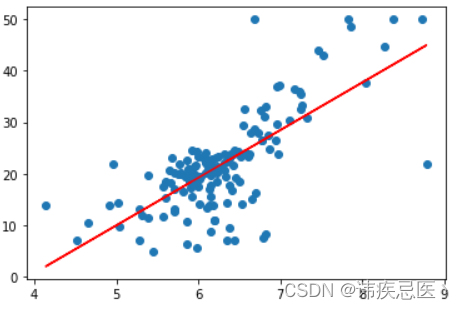
plt.scatter(x_train[:,5],y_train)
plt.plot(x_train[:,5],a*x_train[:,5]+b,c='r')
plt.show()

1.4、使用sklearn实现一元线性回归

from sklearn.linear_model import LinearRegression
lr = LinearRegression()
lr.fit(x_train[:,5].reshape(-1,1),y_train)
y_predict = lr.predict(x_test[:,5].reshape(-1,1))

plt.scatter(x_test[:,5],y_test)
plt.plot(x_test[:,5],y_predict,c='r')
plt.show()

2、多元线性回归

参考链接

线性回归是评估自变量x和应变量y之间的一种线性关系，当只有一个自变量称为一元线性回归，多个自变量称为多元线性回归，现实生活中数据都是比较复杂的，比如影响房价的因素往往不止一个，可能还有附近地铁，房间数，层数，建筑年代等诸多因素。不过每个因素对房价影响权重不同，因此我们可以用多个权重来表示多个因素与房屋价格的关系

x：影响因素，即特征。
w：每个x的影响力度。
n：特征的个数。
y^：房屋的预测价格。
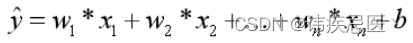
在这里插入图片描述

在这里插入图片描述
这样，就可以表示为：
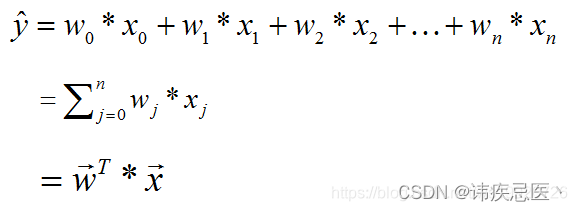
在这里插入图片描述

多元线性回归在空间中，可以表示为一个超平面，去拟合空间中的数据点。
我们的目的就是从现有的数据中，去学习w与b的值。一旦w与b的值确定，就能够确定拟合数据的线性方程，这样就可以对未知的数据x进行预测y（房价）

损失函数：
对于机器学习来讲，就是从已知数据去建立一个模型，使得该模型能够对未知数据进行预测。实际上，机器学习的过程就是确定模型参数的过程。
对于监督学习来说，我们可以通过建立损失函数来实现模型参数的求解，损失函数也称目标函数或代价函数，简单来说就是关于误差的一个函数。损失函数用来衡量模型预测值与真实值之间的差异。机器学习的目标，就是要建立一个损失函数，使得该函数的值最小。
也就是说，损失函数是一个关于模型参数的函数（以模型参数w作为自变量的函数），自变量可能的取值组合通常是无限的，我们的目标，就是要在众多可能的组合中，找到一组最合适的自变量组合，使得损失函数的值最小。
在线性回归中，我们使用平方损失函数（最小二乘法），定义如下：
在这里插入图片描述

2.2、使用sklearn实现多元线性回归

多元线性回归没办法通过画图看出效果，但是可以通过score来获取模型的评分。
注意：多元线性回归是不需要归一化的，学习的是各自维度特征

# 使用boston数据集 
import numpy as np
import matplotlib.pyplot as plt
import sklearn
from sklearn.model_selection import train_test_split
import pandas as pd 

# 加载波士顿房屋数据集
data_url = "http://lib.stat.cmu.edu/datasets/boston"
raw_df = pd.read_csv(data_url, sep="\s+", skiprows=22, header=None)
data = np.hstack([raw_df.values[::2, :], raw_df.values[1::2, :2]])
target = raw_df.values[1::2, 2]

x_train,x_test,y_train,y_test = train_test_split(data,target,test_size=0.3,random_state=233)
lr = LinearRegression()
lr.fit(x_train,y_train)
lr.score(x_test,y_test)

2.3、MSE

MSE（Mean Squared Error），平均平方差，为所有样本数据误差（真实值与预测值之差）的平方和，然后取均值。越接近0越好，mse越小容易出现过拟合，反之容易欠拟合。
在这里插入图片描述

手动实现

mse = np.sum(((y_test-y_predict)**2)/len(y_test))
mse

使用skleran实现

# 使用sklearn实现
from sklearn.metrics import mean_squared_error
mean_squared_error(y_test,y_predict)

2.4、RMSE

RMSE（Root Mean Squared Error），平均平方误差的平方根，即在MSE的基础上，取平方根。放大了较大误差之间的差距
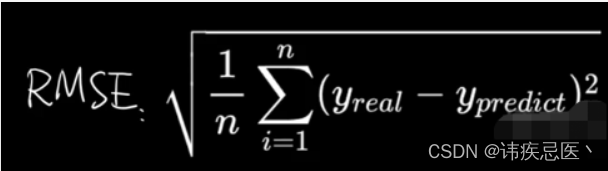
在这里插入图片描述

#RMSE，先对数据进行了平方然后累加在开方，放大了较大误差之间的差距
rmse = np.sqrt(mse)

# 使用skleran实现
from sklearn.metrics import mean_squared_error
mean_squared_error(y_test,y_predict,squared=False)

2.5、MAE

MAE（Mean Absolute Error），平均绝对值误差，为所有样本数据误差的绝对值和，然后去均值。真实误差
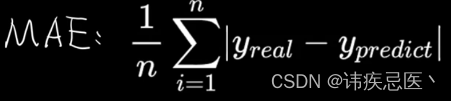
在这里插入图片描述

# MAE 真是误差
mae = np.sum((np.abs(y_test-y_predict))/len(y_test))

# 使用skleran实现
from sklearn.metrics import mean_absolute_error
mean_absolute_error(y_test,y_predict)

2.6、R^2

R2为决定系数，用来表示模型拟合性的分值，值越高表示模型拟合性越好，在训练集中，R2的取值范围为[0,1]。在R2的取值范围为[-∞,1]。从公式定义可知，最理想情况，所有的样本数据的预测值与真实值相同，即RSS为0，此时R2为1。
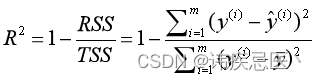
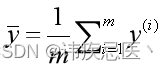
在这里插入图片描述
在这里插入图片描述

r2 = 1 - (np.sum((y_test-y_predict)**2))/(np.sum((y_test-np.mean(y_test))**2))
r2

公式二：消除样本本身取值大小的影响，实现了归一化
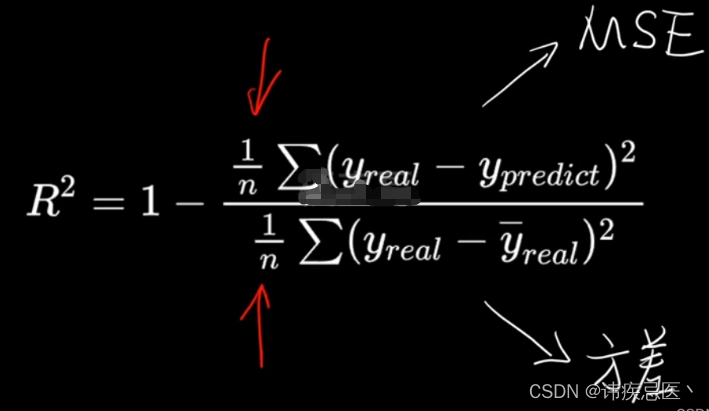
在这里插入图片描述

1-mse/np.var(y_test)

# skleran实现
from sklearn.metrics import r2_score
r2_score(y_test,y_predict)

2.7、模型评价方法总结

总结：MSE计算简单，RMSE和MAE保持了和样本同样的量纲，MSE和MAE适用误差相对明显的时候，大的误差就会有比较大的权重，RMSE针对误差不是很明显的时候，MAE相比MSE更能凸显异常值，在回归模型中损失函数一般使用MAE、MSE、RMSE，性能评估指标一般使用R^2。

3、多项式回归代码实现

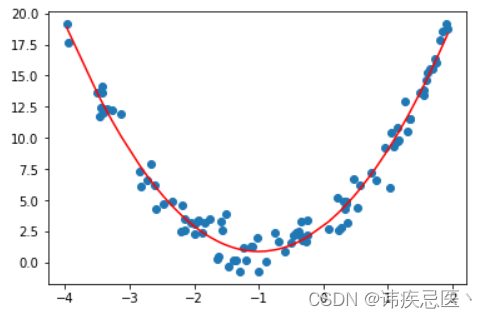
对于非线性回归的数据，我们可以使用多项式回归拟合一条曲线。

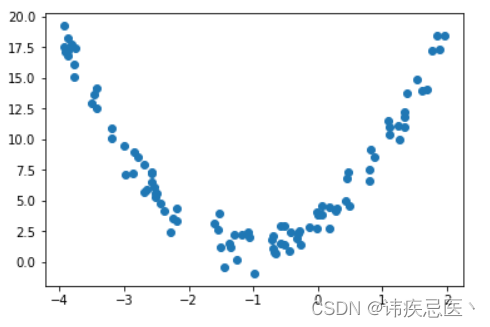
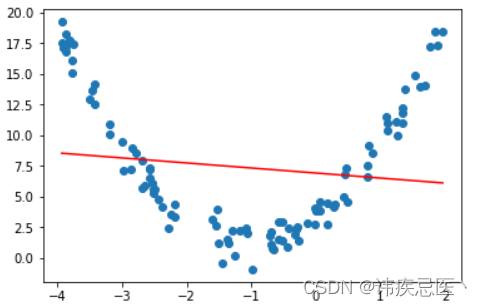
在这里插入图片描述
在这里插入图片描述

可以明显看到使用直线拟合非线性数据，效果非常不好。

# 多项式回归
x = np.random.uniform(-4,2,size=(100))
y = 2*x**2 + 4*x+3+np.random.randn(100)
X = x.reshape(-1,1)
plt.scatter(x,y)
plt.show()

lr = LinearRegression()
lr.fit(X,y)
y_predict = lr.predict(X)
plt.scatter(x,y)
plt.plot(np.sort(x),y_predict[np.argsort(x)],color='red')
plt.show()

使用多项式回归拟合
在这里插入图片描述

X_new = np.hstack([X,X**2])
lr = LinearRegression()
lr.fit(X_new,y)
y_predict = lr.predict(X_new)
plt.scatter(x,y)
plt.plot(np.sort(x),y_predict[np.argsort(x)],color='red')
plt.show()+# 输出函数截取
lr.intercept_
# 输出函数特征值
lr.coef_

使用sklearn实现

# 使用sklearn实现
from sklearn.preprocessing import PolynomialFeatures
# 最高2次幂
polynomial = PolynomialFeatures(degree=2)
# 转换后的特征
x_poly = polynomial.fit_transform(X)
lr = LinearRegression()
lr.fit(x_poly,y)
y_predict = lr.predict(x_poly)
plt.scatter(x,y)
plt.plot(np.sort(x),y_predict[np.argsort(x)],color='red')
plt.show()

4、逻辑回归解决分类问题

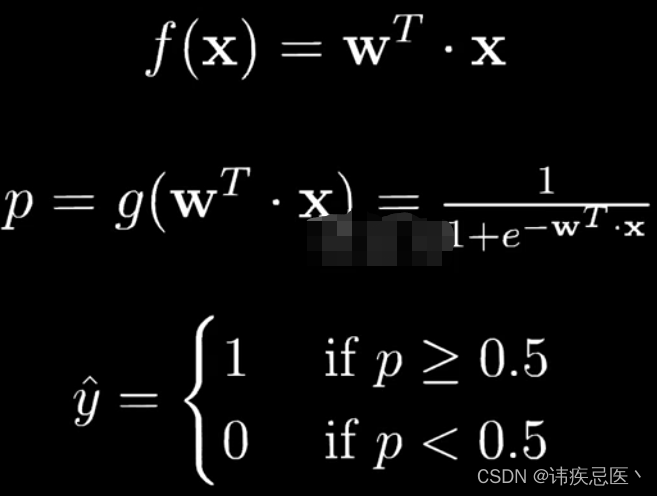
在这里插入图片描述
误差距离计算方式：
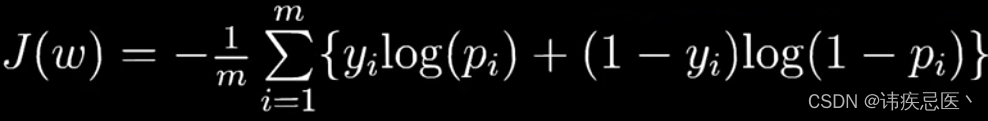
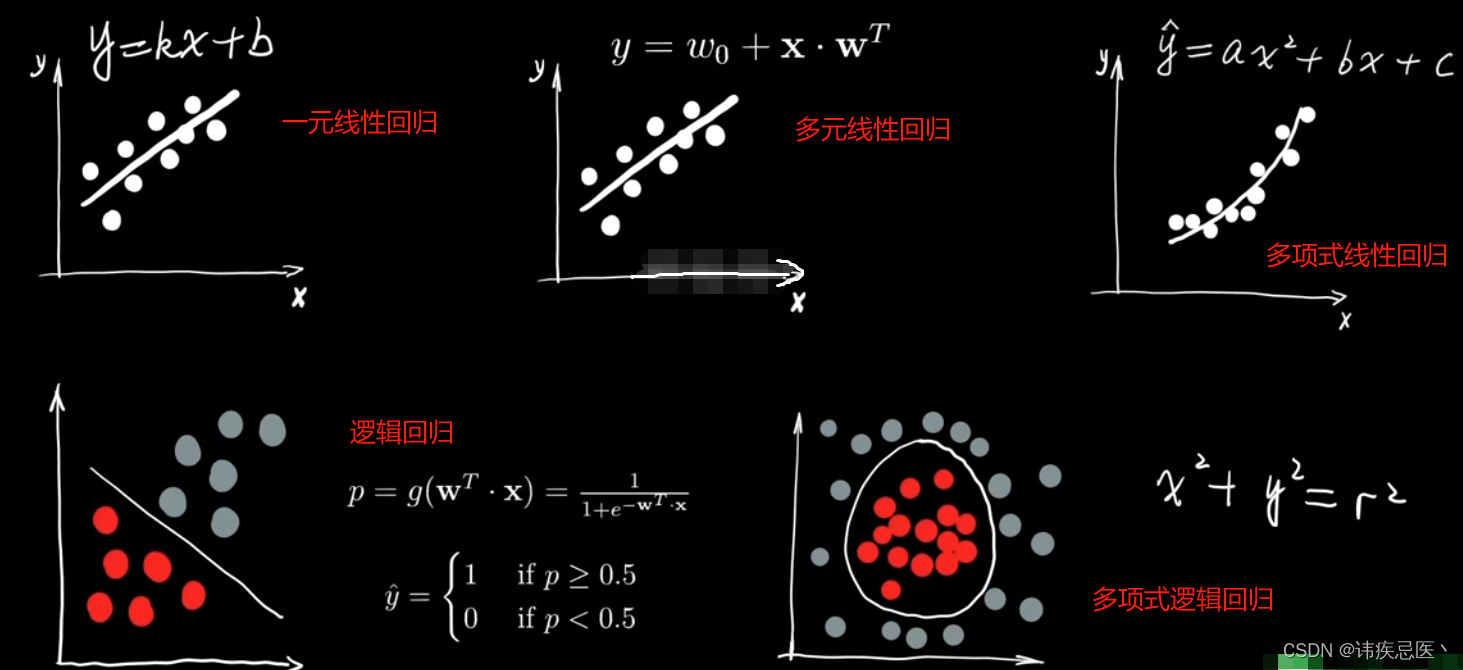
在这里插入图片描述
在这里插入图片描述

在这里插入图片描述

4.2、使用sklearn实现逻辑回归

# 逻辑回归
import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.datasets import make_classification
x,y = make_classification(
    n_samples=200,# 样本数
    n_features=2,# 特征数
    n_redundant=0,# 冗余特指数
    n_classes=2,# 类型
    n_clusters_per_class=1,# 族设为1
    random_state=1024
)
x.shape,y.shape

x_train,x_test,y_train,y_test = train_test_split(x,y,train_size=0.7,random_state=1024,stratify=y)
plt.scatter(x_train[:,0],x_train[:,1],c=y_train)

from sklearn.linear_model import LogisticRegression
clf = LogisticRegression()
clf.fit(x_train,y_train)
clf.score(x_test,y_test)
clf.predict(x_test)

4.3、超参数使用

# 超参数
from sklearn.model_selection import GridSearchCV
params = [{
    'penalty':['l2','l1'],# 损失函数正则项
    'C':[0.0001,0.001,0.01,0.1,1,10,100,1000],
    'solver':['liblinear']# 优化算法
},{
    'penalty':['none'],
    'C':[0.0001,0.001,0.01,0.1,1,10,100,1000],
    'solver':['lbfgs']
},{
    'penalty':['elasticnet'],
    'C':[0.0001,0.001,0.01,0.1,1,10,100,1000],
    'l1_ratio':[0,0.25,0.5,0.75,1],
    'solver':['saga'],
    'max_iter':[200]
}]
grid = GridSearchCV(
    estimator=LogisticRegression(),
    param_grid=params,
    n_jobs=-1
)

grid.fit(x,y)
grid.best_score_

grid.best_estimator_.score(x_test,y_test)
grid.best_params_

4.4、多项式逻辑回归

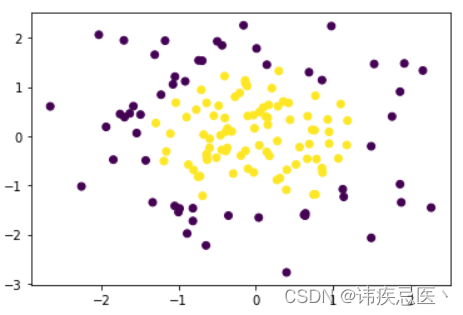
在这里插入图片描述

# 多项式逻辑回归
np.random.seed(0)
X = np.random.normal(0,1,size=(200,2))
y = np.array((X[:,0]**2)+(X[:,1]**2)<2,dtype='int')
x_train,x_test,y_train,y_test = train_test_split(X,y,train_size=0.7,random_state=1024,stratify=y)
plt.scatter(x_train[:,0],x_train[:,1],c=y_train)

from sklearn.preprocessing import PolynomialFeatures
poly = PolynomialFeatures(degree=2)
poly.fit(x_train)

x2 = poly.transform(x_train)
x2t = poly.transform(x_test)
clf = LogisticRegression()
clf.fit(x2,y_train)
clf.score(x2,y_train)
clf.score(x2t,y_test)

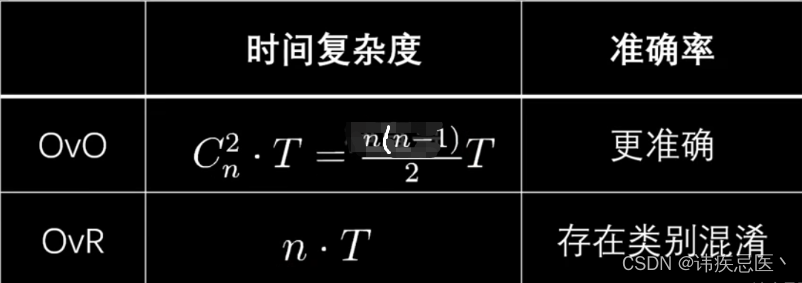
4.5、多分类问题OVR

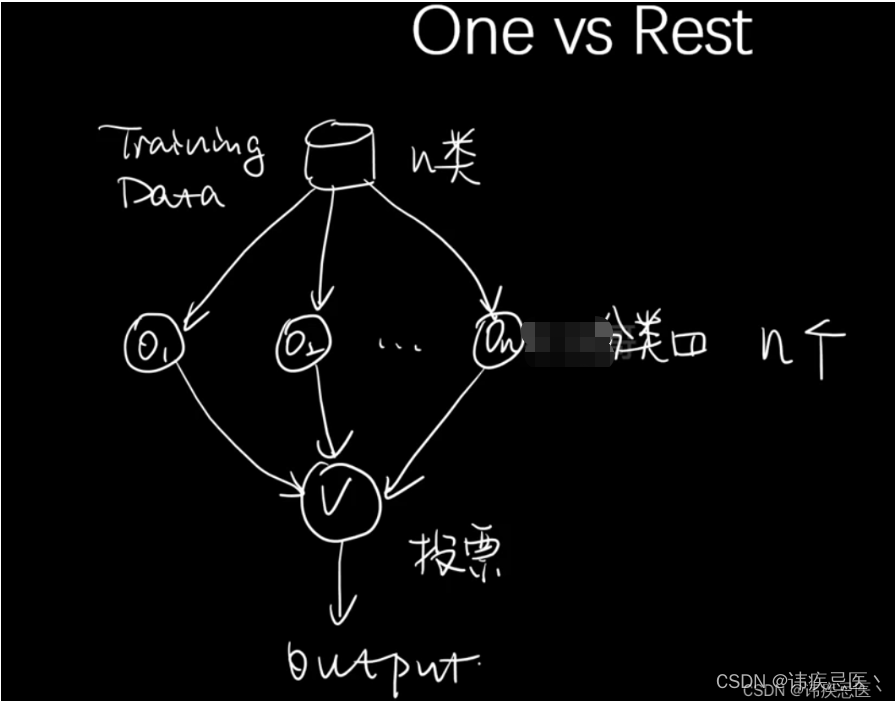
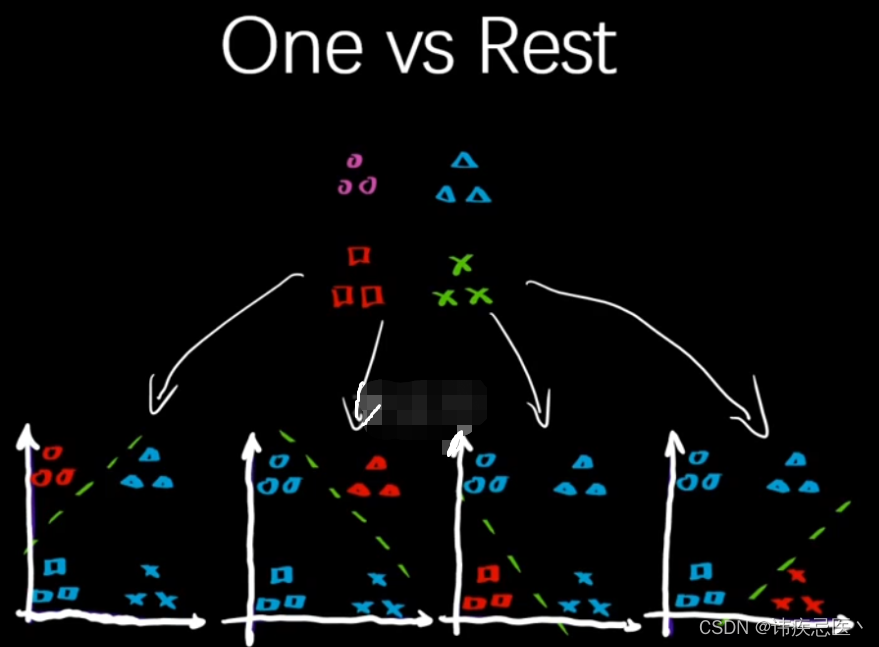
在这里插入图片描述

在这里插入图片描述

# 多分类问题，OVO和OVR
from sklearn import datasets
iris = datasets.load_iris()
x = iris.data
y = iris.target
x_train,x_test,y_train,y_test = train_test_split(x,y,random_state=666)

plt.scatter(x_train[:,0],x_train[:,1],c=y_train)
plt.show()

from sklearn.multiclass import OneVsRestClassifier
ovr = OneVsRestClassifier(clf)
ovr.fit(x_train,y_train)
ovr.score(x_test,y_test)

4.6、多分类问题OVO

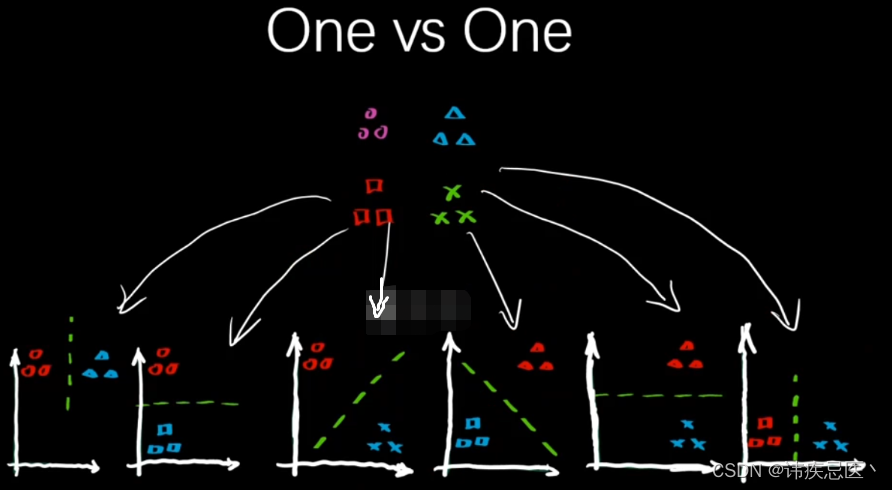
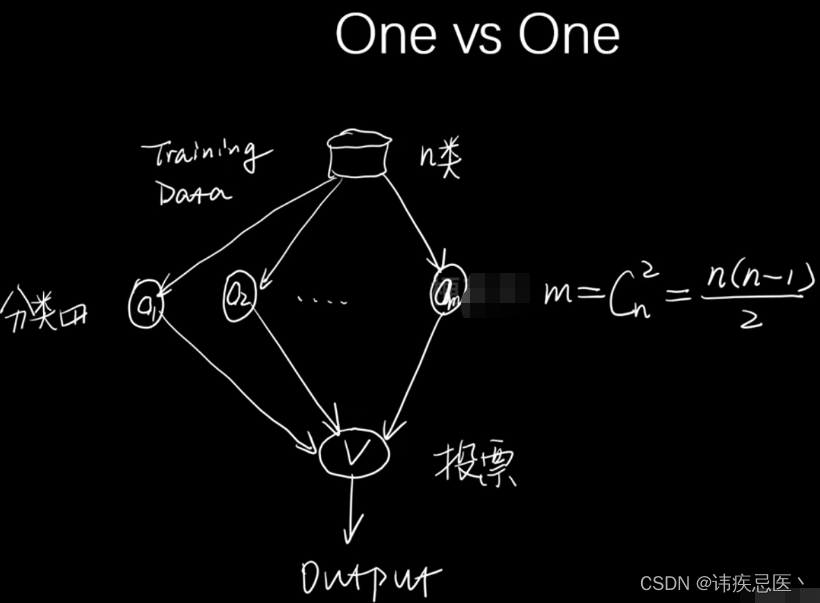
在这里插入图片描述
在这里插入图片描述

# 多分类问题，OVO和OVR
from sklearn import datasets
iris = datasets.load_iris()
x = iris.data
y = iris.target
x_train,x_test,y_train,y_test = train_test_split(x,y,random_state=666)

plt.scatter(x_train[:,0],x_train[:,1],c=y_train)
plt.show()

from sklearn.multiclass import OneVsOneClassifier
ovo = OneVsOneClassifier(clf)
ovo.fit(x_train,y_train)
ovo.score(x_test,y_test)

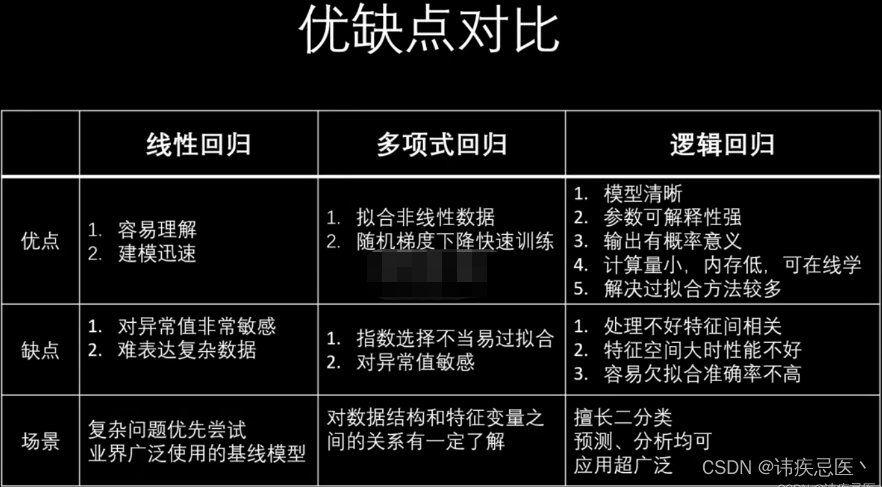
在这里插入图片描述

5、优缺点对比

在这里插入图片描述
KNN对比线性算法：
KNN算法：非参数模型、计算量大、数据无假设
线性算法：可解释性好、建模迅速、线性分布

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1580695.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

HarmonyOS开发实例：【状态管理】

HarmonyOS开发实例：【状态管理】

状态管理 ArkUI开发框架提供了多维度的状态管理机制&#xff0c;和UI相关联的数据&#xff0c;不仅可以在组件内使用&#xff0c;还可以在不同组件层级间传递&#xff0c;比如父子组件之间&#xff0c;爷孙组件之间等&#xff0c;也可以是全局范围内的传递&#xff0c;还可以是…
阅读更多...
【考研数学】1800还是660还是880？

【考研数学】1800还是660还是880？

关于这几本习题册如何选择&#xff0c;肯定是根据他们的不同特点以及我们的需求结合选择&#xff0c;给大家的建议如下&#xff1a; 1800适合初期&#xff0c;可以帮助你熟悉数学公式和基础定义&#xff0c;迅速上手用。刚开始觉得难很正常&#xff0c;存在一个上手的过程&…
阅读更多...
VRRP虚拟路由实验（思科）

VRRP虚拟路由实验（思科）

一&#xff0c;技术简介 VRRP&#xff08;Virtual Router Redundancy Protocol&#xff09;是一种网络协议&#xff0c;用于实现路由器冗余&#xff0c;提高网络可靠性和容错能力。VRRP允许多台路由器共享一个虚拟IP地址&#xff0c;其中一台路由器被选为Master&#xff0c;负…
阅读更多...
【Erlang】【RabbitMQ】Linux（CentOS7）安装Erlang和RabbitMQ

【Erlang】【RabbitMQ】Linux（CentOS7）安装Erlang和RabbitMQ

一、系统环境 查版本对应&#xff0c;CentOS-7&#xff0c;选择Erlang 23.3.4&#xff0c;RabbitMQ 3.9.16 二、操作步骤 安装 Erlang repository curl -s https://packagecloud.io/install/repositories/rabbitmq/erlang/script.rpm.sh | sudo bash安装 Erlang package s…
阅读更多...
扫描IP开放端口该脚本用于对特定目标主机进行常见端口扫描(加载端口字典)或者指定端口扫描,判断目标主机开

扫描IP开放端口该脚本用于对特定目标主机进行常见端口扫描(加载端口字典)或者指定端口扫描,判断目标主机开

扫描IP开放端口该脚本用于对特定目标主机进行常见端口扫描(加载端口字典)或者指定端口扫描,判断目标主机开 #/bin/bash #该脚本用于对特定目标主机进行常见端口扫描(加载端口字典)或者指定端口扫描,判断目标主机开放来哪些端口 #用telnet方式 IP$1 #IP119.254.3.28 #获得IP的前…
阅读更多...
【STL】顺序容器与容器适配器

【STL】顺序容器与容器适配器

文章目录 1顺序容器概述1.1array1.2forward_list1.3deque 2.如何确定使用哪种顺序容器呢&#xff1f;3.容器适配器的概念4.如何定义适配器呢&#xff1f; 1顺序容器概述 给出以下顺序容器表&#xff1a; 顺序容器类型作用vector可变大小的数组&#xff0c;支持快速访问&#…
阅读更多...
UML学习

UML学习

UML(Unified Modeling Language)&#xff1a;统一建模语言&#xff0c;提供了一套符号和规则来帮助分析师和设计师表达系统的架构、行为和交互 类图&#xff1a;描绘类、接口之间的关系(继承、实现、关联、依赖等)以及类的内部结构(属性和方法)&#xff0c;直观展现系统的静态…
阅读更多...
2024年3月电子学会青少年软件编程 中小学生Python编程等级考试一级真题解析（判断题）

2024年3月电子学会青少年软件编程 中小学生Python编程等级考试一级真题解析（判断题）

2024年3月Python编程等级考试一级真题解析 判断题&#xff08;共10题&#xff0c;每题2分&#xff0c;共20分&#xff09; 26、turtle 画布的坐标系原点是在画布的左上角 答案&#xff1a;错 考点分析&#xff1a;考查turtle相关知识&#xff0c;turtle画布坐标系是在画布的…
阅读更多...
c# wpf LiveCharts 饼图 简单试验

c# wpf LiveCharts 饼图 简单试验

1.概要 c# wpf LiveCharts 饼图 简单试验 2.代码 <Window x:Class"WpfApp3.Window5"xmlns"http://schemas.microsoft.com/winfx/2006/xaml/presentation"xmlns:x"http://schemas.microsoft.com/winfx/2006/xaml"xmlns:d"http://schem…
阅读更多...
openharmony launcher 调研笔记（03）UI 数据装配

openharmony launcher 调研笔记（03）UI 数据装配

最近在看launcher&#xff0c;把自己调研的点做个笔记&#xff0c;持续修改更新中&#xff0c;个人笔记酌情参考。 桌面上半部分包含父子逻辑&#xff1a; Column() { PageDesktopLayout(); } PageDesktopLayout->GridSwiper->Swiper->SwiperPage 1.PageDe…
阅读更多...
即插即用篇 | RTDETR引入Haar小波下采样 | 一种简单而有效的语义分割下采样模块

即插即用篇 | RTDETR引入Haar小波下采样 | 一种简单而有效的语义分割下采样模块

本改进已集成到 RT-DETR-Magic 框架。 下采样操作如最大池化或步幅卷积在卷积神经网络（CNNs）中被广泛应用，用于聚合局部特征、扩大感受野并减少计算负担。然而，对于语义分割任务，对局部邻域的特征进行池化可能导致重要的空间信息丢失，这有助于逐像素预测。为了解决这个问…
阅读更多...
Collection与数据结构 二叉树(一):二叉树的性质与基本操作

Collection与数据结构 二叉树(一):二叉树的性质与基本操作

1. 树形结构 1.1 概念1 (了解) 树是一种非线性的数据结构&#xff0c;它是由n&#xff08;n>0&#xff09;个有限结点组成一个具有层次关系的集合。把它叫做树是因为它看起来像一棵倒挂的树&#xff0c;也就是说它是根朝上&#xff0c;而叶朝下的。它具有以下的特点&#…
阅读更多...
已解决：windows 下无法加载文件 xxx.ps1，因为在此系统上禁止运行脚本

已解决：windows 下无法加载文件 xxx.ps1，因为在此系统上禁止运行脚本

目录 1&#xff0c;问题描述2&#xff0c;问题解决 1&#xff0c;问题描述 当通过 npm 全局安装依赖后&#xff08;比如 ts 对应的 tsc 命令&#xff0c;还有 pnpm&#xff09;&#xff0c;想直接使用安装的命令&#xff0c;就会报错&#xff1a; 2&#xff0c;问题解决 以管…
阅读更多...
《QT实用小工具·二十二》多种样式导航按钮控件

《QT实用小工具·二十二》多种样式导航按钮控件

1、概述 源码放在文章末尾 该项目实现了多种样式的导航按钮控件 可设置文字的左侧、右侧、顶部、底部间隔。 可设置文字对齐方式。 可设置显示倒三角、倒三角边长、倒三角位置、倒三角颜色。 可设置显示图标、图标间隔、图标尺寸、正常状态图标、悬停状态图标、选中状态图标…
阅读更多...
P5356 [Ynoi2017] 由乃打扑克

P5356 [Ynoi2017] 由乃打扑克

我手把手教她打扑克 qwq 综合分析一下2个操作&#xff0c;查找区间第k小的值&#xff0c;感觉可以用主席树&#xff0c;区间修改那没事了 考虑分块做法,块长B 分析第一个操作 只需要维护数列的单调性&#xff0c;然后二分答案上二分就ok了 分析第二个操作 维护一个加法懒…
阅读更多...
比较好玩的车子 高尔夫6

比较好玩的车子 高尔夫6

https://www.sohu.com/a/484063087_221273 四万多如愿收获手动挡高尔夫6&#xff0c;可靠性、经济性、操控性兼顾_搜狐汽车_搜狐网 2.基本上其他人也不知道到底是什么相关的车子信息
阅读更多...
HarmonyOS 开发-自定义视图实现Tab效果

HarmonyOS 开发-自定义视图实现Tab效果

介绍 本示例介绍使用Text、List等组件&#xff0c;添加点击事件onclick,动画&#xff0c;animationTo实现自定义Tab效果。 效果预览图 使用说明 点击页签进行切换&#xff0c;选中态页签字体放大加粗&#xff0c;颜色由灰变黑&#xff0c;起到强调作用&#xff0c;同时&…
阅读更多...
鸿蒙HarmonyOS开发实例：【简单时钟】

鸿蒙HarmonyOS开发实例：【简单时钟】

简单时钟 介绍 本示例通过使用[ohos.display]接口以及Canvas组件来实现一个简单的时钟应用。 效果预览 主页 使用说明 1.界面通过setInterval实现周期性实时刷新时间&#xff0c;使用Canvas绘制时钟&#xff0c;指针旋转角度通过计算得出。 例如&#xff1a;"2 * M…
阅读更多...
第十课 Excel

第十课 Excel

最上方标题栏&#xff1a; 显示共工作薄名称&#xff0c;如果显示兼容模式是没有办法使用高级功能的。分辨高版本和低版本可以通过后缀名进行分辨&#xff1b;显示xlsx就是高版本工作薄&#xff0c;如果显示xls的话就是低版本工作薄了。如果同事老板都使用的是低版本的话我们发…
阅读更多...
【攻防世界】Web_python_template_injection

【攻防世界】Web_python_template_injection

{{}}是变量包裹标识符&#xff0c;里面存放的是一个变量&#xff0c;当你输入 http://61.147.171.105:55121/{{8*8}} 执行成功&#xff0c;说明存在模版注入。接下来&#xff0c;开始想办法编代码拿到服务器的控制台权限 。 首先&#xff0c;题目告诉我们这是一个 python 注入…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023