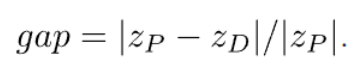文章目录
- 前言
- 从Cutting stock problem说起
- 常规建模
- Column generation reformulation
- 列生成法
- 核心思想
- 相关概念
- Master Problem (MP)
- Linear Master Problem (LMP)
- Restricted Linear Master Problem (RLMP)
- subproblem(核能预警,非常重要)
- 算法流程图
- CG求解cutting stock problem
- 适用场景:large linear programming
- 参考资料
前言
学习列生成之前,有一些前置基础需要理解,不然就没法继续往下学了。所以为了写这篇文章,我提前铺垫了3篇文章帮助自己把基础捡起来!
- 单纯形法:运筹学基础(一)求解线性规划的单纯形法详解
- 检验数:运筹学基础(四):单纯形法中检验数(reduced cost)的理解
- 对偶问题:运筹学基础(五):对偶问题及其性质
今天终于可以进入正题了!
从Cutting stock problem说起
有一堆固定长度的钢管,不同的顾客想要长度不一样的钢管若干,怎么切割钢管能够使得消耗的钢管数最少?

常规建模
【集合】
- K K K:未切割的钢管集合;
- I I I:所需钢管的种类集合;
【参数】
- D i D_i Di:第 i i i种钢管的需求数量;
- L k L_k Lk:第 k k k根未切钢管的长度;
- L i L_i Li:第 i i i种钢管的长度;
【决策变量】
- x k i x_{ki} xki:第 k k k根钢管切割第 i i i种长度的数量;
- y k y_k yk:第 k k k根钢管是否使用;
【数学模型】
目标函数:最小化使用的钢管数量
约束条件:
- 每根钢管被切割的总长度,不多于该根钢管的总长度;
- 每种钢管被切割的数量不低于该种钢管的总需求量;
m i n ∑ k ∈ K y k s . t . ∑ i ∈ I x k i L i ≤ L k ∗ y k , ∀ k ∈ K ∑ k ∈ K x k i ≥ D i , ∀ i ∈ I x k i ∈ { 0 , 1 } , ∀ k ∈ K , i ∈ I y k ∈ { 0 , 1 } , ∀ k ∈ K min \quad \sum_{k\in K}y_k\\ s.t. \sum_{i\in I}x_{ki}L_i\leq L_k*y_k, \forall k \in K\\ \sum_{k\in K}x_{ki} \geq D_i, \forall i \in I\\ x_{ki} \in \{0, 1\}, \forall k\in K, i\in I\\ y_{k} \in \{0, 1\}, \forall k\in K mink∈K∑yks.t.i∈I∑xkiLi≤Lk∗yk,∀k∈Kk∈K∑xki≥Di,∀i∈Ixki∈{0,1},∀k∈K,i∈Iyk∈{0,1},∀k∈K
问题:该建模方式求解不高效(怎么理解),因此有人想出了第二种建模思路。
Column generation reformulation
假设所有的切割方式已知,我们用:
- P P P表示所有的切割方案集合;
- C p i C_{pi} Cpi表示在第 p p p种切割方式下,能切割出的第 i i i种钢管的数量;
定义新的决策变量:
- z p z_p zp:表示执行第 p p p种切割模式的钢管的数量。
数学模型表示如下:
m
i
n
∑
p
∈
P
z
p
s
.
t
.
∑
p
∈
P
C
p
i
z
p
≥
D
i
,
∀
i
∈
I
z
p
≥
0
,
z
p
i
s
i
n
t
e
g
e
r
,
∀
p
∈
P
min \sum_{p\in P}z_p\\ s.t. \sum_{p\in P}C_{pi}z_p \geq D_i, \forall i \in I\\ z_p \geq 0, z_p \quad is \quad integer, \forall p\in P
minp∈P∑zps.t.p∈P∑Cpizp≥Di,∀i∈Izp≥0,zpisinteger,∀p∈P
核心问题:切割模式非常多,穷举出来几乎是不可能的,也没有必要(因为不是所有的切割模式都会被用到)!那么如何去寻找最优的切割模式呢?
铛铛铛铛,列生成法正式登场!
列生成法
核心思想
列生成法本质上也是单纯形法的一种形式。常规的单纯形法要求可以把所有变量显式的表达出来,但是诸如cutting stock problem之类的问题,可能无法做到这一点,因此常规的单纯形法就束手无策了。
回想一下单纯形法的迭代过程,基变量的个数等于约束的个数,每次找一个非基变量入基(这个非基变量的增加,要能优化目标函数),直到不能改善目标函数值为止。可以发现,在这个过程中,并不是所有的变量都会用到!
因此有人想到:
- 可以先把原问题( P 0 P_0 P0)限制( r e s t r i c t restrict restrict)到一个规模很小的问题( P 1 P_1 P1)上,然后用单纯形法求解 P 1 P_1 P1。但此时求的最优解是 P 1 P_1 P1的最优解,不是原问题的最优解。
- 因此还需要一个子问题(subproblem)去检查是否存在一个非基变量,其reduced cost小于0(即改变量的增大可以进一步优化目标函数),如果存在,就把这个非基变量相关的系数列加入到 P 1 P_1 P1的系数矩阵中,回到第一步。直到找不到reduced cost小于0的非基变量,即找到了原问题的最优解。
为了获取更优的目标值,往往会选择reduced cost最小的非基变量(切割模式)加入到 P 1 P_1 P1中,那么如何寻找reduced cost最小的非基变量呢?
回答这个问题之前,有一些相关概念先快速弄清楚。
相关概念
Master Problem (MP)
对于一般问题而言,如果要用CG(column generation)求解,一般要转化成set covering model,类似于上面的cutting stock model。不是很理解为什么
转为称为set covering model的问题就称为MP,例如:

Linear Master Problem (LMP)
如果MP里存在整数变量,要先进行线性松弛,MP线性松弛以后的问题就是LMP。

Restricted Linear Master Problem (RLMP)
将LMP限制(restrict)到一个规模更小(即变量数量更少)的问题,就称为RLMP了。
可以看到,下式相比原来的linear master problem,restricted linear master problem相当于把
y
k
+
1
.
.
.
y
n
y_{k+1}...y_{n}
yk+1...yn强制限制为非基变量了。

subproblem(核能预警,非常重要)
subproblem就是帮助我们找到,当前是否还有非基变量加入 P 1 P_1 P1能够使得目标函数值进一步改善的。理解subproblem的前提是,弄清楚检验数和对偶变量之间的关系。
我们做一下推导:

假设我们找到了原问题的最优解
[
x
B
,
0
]
[x_B, 0]
[xB,0],那么此时原问题的检验数一定都是大于等于0的,即:
C
N
T
−
C
B
T
B
−
1
N
≥
0
C_N^T-C_B^TB^{-1}N \geq 0
CNT−CBTB−1N≥0
可以得到:
C
N
T
≥
C
B
T
B
−
1
N
C_N^T \geq C_B^TB^{-1}N
CNT≥CBTB−1N
我们计算一下:
C
B
T
B
−
1
A
=
C
B
T
B
−
1
[
B
,
N
]
=
[
C
B
T
,
C
B
T
B
−
1
N
]
≤
[
C
B
T
,
C
N
T
]
=
C
T
C_B^TB^{-1}A=\\ \quad\\ C_B^TB^{-1}[B, N]=\\ \quad\\ [C_B^T, C_B^TB^{-1}N]\leq\\ \quad\\ [C_B^T,C_N^T]=\\ \quad\\ C^T
CBTB−1A=CBTB−1[B,N]=[CBT,CBTB−1N]≤[CBT,CNT]=CT
提炼一下上式推导过程中的首尾:
C
B
T
B
−
1
A
≤
C
T
C_B^TB^{-1}A \leq C^T
CBTB−1A≤CT
观察一下对偶问题的约束条件:
y
T
A
≤
C
T
y^TA\leq C^T
yTA≤CT
发现:
C
B
T
B
−
1
C_B^TB^{-1}
CBTB−1
是对偶问题的一个可行解!
我们继续证明它不仅是一个可行解,而且是最优解:
令:
y
T
=
C
B
T
B
−
1
y^T=C_B^TB^{-1}
yT=CBTB−1
此时对偶问题的目标函数值为:
y
T
A
=
C
B
T
B
−
1
b
=
y^TA=C_B^TB^{-1}b=
yTA=CBTB−1b=
这里有个转换是:
x
B
=
B
−
1
b
x_B=B^{-1}b
xB=B−1b
在我的文章运筹学基础(四):单纯形法中检验数(reduced cost)的理解里有相关推导。
因此:
y
T
A
=
C
B
T
B
−
1
b
=
C
B
T
x
B
=
C
T
x
y^TA=C_B^TB^{-1}b=C_B^Tx_B=C^Tx
yTA=CBTB−1b=CBTxB=CTx
根据对偶问题的最优性性质,可知
y
T
y^T
yT为对偶问题的最优解。
于是检验数的表达式可以写成:
C
N
T
−
C
B
T
B
−
1
N
=
y
T
N
C_N^T-C_B^TB^{-1}N = y^TN
CNT−CBTB−1N=yTN
所谓的subproblem就是根据该公式,在 y k + 1 . . . y n y_{k+1}...y_{n} yk+1...yn中找到检验数为负,并且最小的非基变量,将变量对应的那一列添加到RLMP中。
算法流程图

CG求解cutting stock problem
题目如下:

第一步:求解RLMP的最优解

第二步:求解subproblem
c
i
c_i
ci表示在新的这种切割模式下,切割第
i
i
i种钢管的数量。
23+27=20米,正好为钢管的总长度,符合条件。

第三步:加入新的切割模式到原来的模型中,继续求解

第四步:继续求解subproblem,无更好的切割模式,终止

适用场景:large linear programming
约束的数量有限,但是变量的数量非常多的大规模线性规划问题。例如:机组人员调度问题(Crew Assignment Problem)、切割问题(Cutting Stock Problem)、车辆路径问题(Vehicle Routing Problem)、单资源工厂选址问题(The single facility location problem )等。
参考资料
- 带你彻底了解Column Generation(列生成)算法的原理
- 大规模优化求解器-Gurobi-教程