中心极限定理
中心极限定理提出了:无论总体服从什么分布,只要n充分大,那么样本均值分布就接近正态分布。
样本的数量越大,取样次数越多,样本平均值的分布也就越接近于一条正态分布曲线。普遍的经验是,样本的数量必须超过30,中心极限定理才能成立。
中心极限定理有两个要点:
- 样本的平均值与总体的平均值类似;
- 样本的平均值呈现正态分布。

Python 代码验证
import numpy.random as np
import seaborn as sns
import matplotlib.pyplot as plt
population_size = 1000000 #总体数量
population = np.rand(1000000)
#查看总体情况
plt.xticks(fontsize=14)
plt.yticks(fontsize=14)
sns.distplot(population,bins=int(180/5),hist = True,kde = False)
plt.title('Histogram of population ',fontsize=20)
plt.xlabel('population',fontsize=20)
plt.ylabel('Count',fontsize=20)
- 总体分布情况
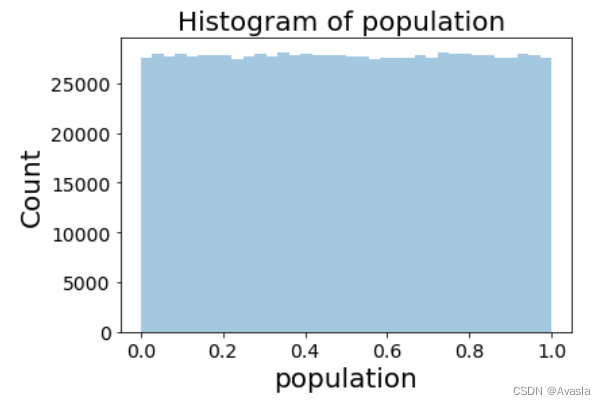
number_of_samples = 10000 #抽样次数
sample_means = np.rand(number_of_samples ) #随机初始化样本均值
sample_size = 2 #样本量n
#抽样
c = np.rand(number_of_samples)
for i in range(0,number_of_samples): #运行10000次循环抽样
c = np.randint(1,population_size,sample_size) #随机抽取1-population_size之间的整数
sample_means[i] = population[c].mean() #计算样本均值并储存到 sample_mean中
#画图
plt.subplot(1,2,1)
plt.xticks(fontsize=14)
plt.yticks(fontsize=14)
sns.distplot(sample_means,bins=int(180/5),hist = True,kde = False)
plt.title('Histogram of Sample mean',fontsize=20)
plt.xlabel('Sample mean',fontsize=20)
plt.ylabel('Count',fontsize=20)
plt.subplot(1,2,2)
plt.xticks(fontsize=14)
plt.yticks(fontsize=14)
sns.distplot(sample_means,hist = False,kde = True)
plt.title('Density of Sample mean',fontsize=20)
plt.xlabel('Sample mean',fontsize=20)
plt.ylabel('Density',fontsize=20)
plt.subplots_adjust(bottom=0.1, right=2, top=0.9)
- Sample Size =1
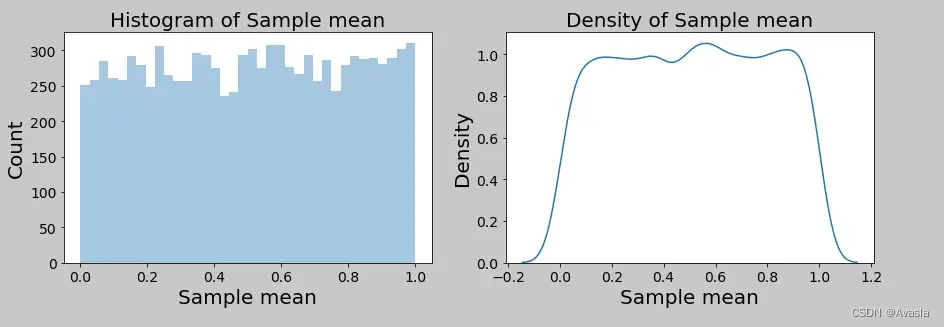
-Sample size =2
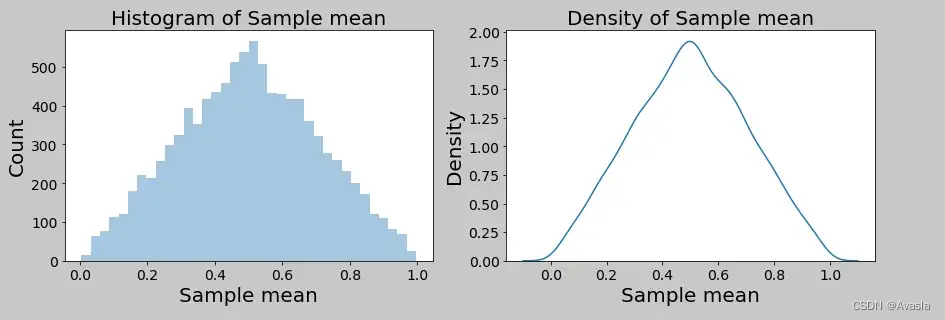
- Sample size =30

百度百科:中心极限定理
MBA智库:中心极限定理
Verifying Central Limit Theorem using Python