目录
1 什么是F检验 F-test
1.1 F-test的定义
1.1.1 维基百科对F检验的定义
1.1.2 百度百科的定义
1.2 F检验的别名
1.3 F检验的判断手段 / 要达成的目标 / 适用范围
1.3.1 判断手段
1.3.2 对H0原假设的理解
1.3.3 判断目标/目的
1.3.4 适用的范围,场合
1.3.5 和其他检验的关系
2 如何弄懂F检验,需要倒推,先理解 F分布和F检验量
2.1 逻辑关系:(倒推需求)F检验→F分布→ F检验量
2.2 为什么?
3 F统计量的构造
3.1 F值/ F指标/ F统计量是如何构造的
3.1.1 构建F值的3个关键参数
3.1.2 F指标的定义
3.1.3 F值 是如何构造出来的?--简单视角
3.1.4 F值 是如何构造出来的?
3.1.5 F值 是如何构造出来的? F=组间误差/组内误差=(SSA/dfa) / (SSE/dfe)
3.2 F统计量和F分布的关系
4 什么是F分布
4.1 F分布的定义
4.1.1 维基百科的定义
4.1.2 来自百度百科的定义
4.3 检验的原理
4.4 F检验的实操(手工方法):根据dfA,dfE 和显著度α 查表得P值, 然后比较2个P值
4.4.1 显著度 α
4.4.2 自由度1=分子自由度=df1=dfA =自变量个数
4.4.3 自由度2=分母自由度=df2=dfE=n-k-1 = 样本总数- xi对应得参数ai个数- 截距1个参数
4.4.4 总自由度,dfT=dfA+dfE
4.4.5 用前面3个值来查表,获得查表的F值,然后比较2个F值
4.5 F检验:计算机的方法,直接求得具体P值,再比较p和 α
5 F统计量的几个公式分析对比
5.1 F值构造的简单视角,便于理解
5.2 F=回归的均方差MS/ 残差的卷方差MS
5.2 F=组间波动/组内波动
5.3 SSA/dfA的具体设计
5.3.1 这部分内容引用如下
5.3.2 组间波动SSA 必须引入2个新参数:组间的组数k 和组内样本数量mi
5.3.3 SSE组内波动必须引入2个新参数:组间的组数k 和组内样本数量mi
5.3.4 计算必须用MS,而不能直接用SS,或者SS的平方和
5.3.5 SSA和SSE还要考虑df 自由度的影响
6 实操例子1:F值的计算
7 实操例子2 :详细的F值里SSA 和SSE 计算过程展开
7.1 题目来源
7.2 先计算SSE,这个只需要算每组样本内,每个X和对应均值的误差就可以
7.3 计算SSA,注意是组间的均值差异,只算均值和二次均值之间差异
7.4 计算自由度df
7.5 计算F值
7.6 查表对比F值和查表F值
7.7 结论
1 什么是F检验 F-test
F检验临界值表提供了右尾F检验的临界值。当F检验的统计量大于该值时,我们的F检验结果在统计上是有意义的。
1.1 F-test的定义
1.1.1 维基百科对F检验的定义
https://zh.wikipedia.org/wiki/F%E6%A3%80%E9%AA%8C![]() https://zh.wikipedia.org/wiki/F%E6%A3%80%E9%AA%8C
https://zh.wikipedia.org/wiki/F%E6%A3%80%E9%AA%8C
- F检验 (F-test),亦称联合假设检验(joint hypotheses test)、方差比率检验、方差齐性检验。
- 它是一种在零假设(null hypothesis, H0)之下,统计值服从F-分布的检验。其通常是用来分析用了超过一个参数的统计模型,以判断该模型中的全部或一部分参数是否适合用来估计总体。
- F检验这名称是由美国数学家兼统计学家George W. Snedecor命名,为了纪念英国统计学家兼生物学家罗纳德·费希尔(Ronald Aylmer Fisher)。Fisher在1920年代发明了这个检验和F-分布,最初称为方差比率(Variance Ratio)[1]。
1.1.2 百度百科的定义
F检验_百度百科F检验(F-test),最常用的别名叫做联合假设检验(英语:joint hypotheses test),此外也称方差比率检验、方差齐性检验。它是一种在零假设(null hypothesis, H0)之下,统计值服从F-分布的检验。其通常是用来分析用了超过一个参数的统计模型,以判断该模型中的全部或一部分参数是否适合用来估计母体。F检验这名称是由美国数学家兼统计学家George W. Snedecor命名,为了纪念英国统计学家兼生物学家罗纳德·费雪(Ronald Aylmer Fisher)。Fisher在1920年代发明了这个检验和F分配,最初叫做方差比率(Variance Ratio)。![]() https://baike.baidu.com/item/F%E6%A3%80%E9%AA%8C/9910842?fr=ge_ala
https://baike.baidu.com/item/F%E6%A3%80%E9%AA%8C/9910842?fr=ge_ala
- F检验(F-test),最常用的别名叫做联合假设检验(英语:joint hypotheses test),此外也称方差比率检验、方差齐性检验。
- 它是一种在零假设(null hypothesis, H0)之下,统计值服从F-分布的检验。其通常是用来分析用了超过一个参数的统计模型,以判断该模型中的全部或一部分参数是否适合用来估计母体。
1.2 F检验的别名
- F检验 F-test
- 联合假设检验 joint hypotheses test
- 方差比率检验 variance ratio test
- 方差齐性检验 Homogeneity of variance test
- 就是比较两个目标的方差是否相同/是否存在显著差异?
对应比较:均值齐性检验 T检验和Z检查
- 我觉得T检验和Z检查,都是比较均值差异的,而不是比较方差齐性的。
- 也就是都是比较 均值齐性的, Homogeneity of Average
1.3 F检验的判断手段 / 要达成的目标 / 适用范围
1.3.1 判断手段
- 它是一种在零假设(null hypothesis, H0)之下,判断统计值服从F-分布的检验
- 根据求得的F值查表而得到的P值,判断是否,接受原假设H0
- F检验临界值表提供了右尾F检验的临界值。
- 当F检验的统计量大于该值时,我们的F检验结果在统计上是有意义的。
1.3.2 对H0原假设的理解
- H0 原假设,一般都是假设两者是相同分布 的这种 理想假设。
- 为什么说是理想假设,因为现实的样本里往往一定存在误差,不可能相同。因此这个H0假设是一个理想假设
- 虽然永远无法认识总体,但现实中的我们总是一厢情愿的希望,样本从总体里来是无误差的
- 理想状态:和之前说的,真实值,观测值,预测值这3种基础数据关系里的真实值一样,本质是永远无法观测到的,只存在于我们的大脑的理想国之中,所以我认为这里是需要懂一点哲学形而上的东西的。
- 举例子:均匀骰子是1/6, 均匀硬币是0.5,我们认为抽样的人群能代表世界上所有人,这都是理想值(所谓的“真实值”,只存在于彼岸的真实值。即使有时候算出来刚好相等,那也应该是恰好相等而已)
1.3.3 判断目标/目的
- 以判断该模型中的全部或一部分参数是否适合用来估计总体
1.3.4 适用的范围,场合
适用场合
- 1 最典型的F检验:检验一系列服从正态分布的总体,是否有相同的标准差
- 2 应用于方差分析(ANOVA)
- 3 回归分析
- 4 检验整条回归模型是否具有解释力,此即Overall F检验 (Overall F test) 。
- 5 检验回归模型中特定自变量是否具有解释力,即偏回归系数是否为零,此即偏F检验(Partial F test) 。
1.3.5 和其他检验的关系
- F检验的分子、分母其实各是一个卡方变量除以各自的自由度
- 分子分母也是标准正态分布的变量吧 ,符合N~(0,1)
- F检验用以检验单一变量可否排除于模型外时,即进行只缩减单一变量之偏F检验,F=t**2
2 如何弄懂F检验,需要倒推,先理解 F分布和F检验量
2.1 逻辑关系:(倒推需求)F检验→F分布→ F检验量
- (倒推需求)
- F检验→
- F分布→
- F检验量
2.2 为什么?
呃,不懂原理永远无法理解F检验吧
3 F统计量的构造
要弄清楚F检验,先要弄清楚F分布。而要弄清楚F分布,得先弄清楚F统计量
3.1 F值/ F指标/ F统计量是如何构造的
3.1.1 构建F值的3个关键参数
确定F分布曲线状态,和具体F取值的3个关键指标
- 1 分子的自由度df1=dfA
- 2 分母的自由度df2=dfE
- 3 F=(SSA/dfA) / (SSE/dfE)
3.1.2 F指标的定义


3.1.3 F值 是如何构造出来的?--简单视角
如果做了多次试验,现在得到多组数据,比如是两组
- 离差平方和∑(x-average(x))**2
- 样本标准偏差的平方=均方误差MS = S2=∑(x-average(x))**2/(n-1)
- 两组数据就能得到两个S2值F=S2/S2' (用较小的/较大的?)
- 然后计算的F值与查表得到的F表值比较,如果
- F < F表 表明两组数据没有显著差异;
- F ≥ F表 表明两组数据存在显著差异。
3.1.4 F值 是如何构造出来的?
一文详解F检验 - 知乎F检验是被誉为现代统计学之父的 R.A. Fisher爵士提出、由George W. Snedecor命名的统计检验方法,主要用于方差齐性检验、方差分析等等。本文介绍F检验的如下应用: 方差齐性检验(F-test of equality of variances…![]() https://zhuanlan.zhihu.com/p/139151375?utm_id=0&wd=&eqid=9d65f0b200194e3800000002646de47b
https://zhuanlan.zhihu.com/p/139151375?utm_id=0&wd=&eqid=9d65f0b200194e3800000002646de47b

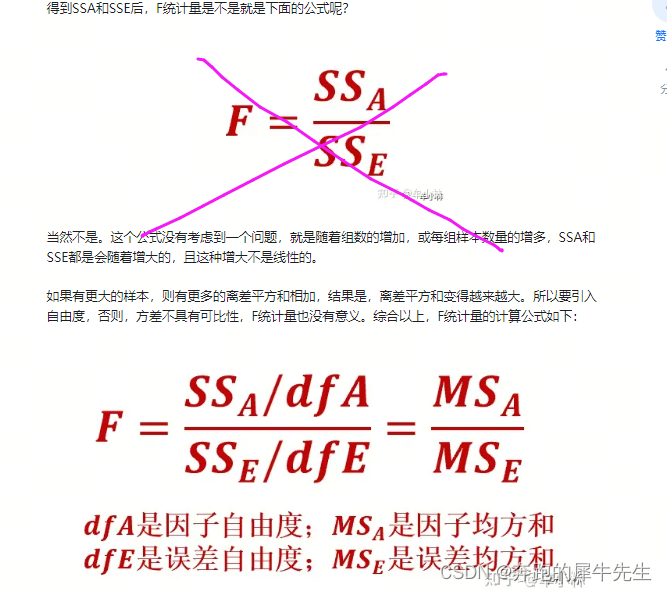
3.1.5 F值 是如何构造出来的? F=组间误差/组内误差=(SSA/dfa) / (SSE/dfe)
F=组间误差/组内误差=(SSA/dfa) / (SSE/dfe)



3.2 F统计量和F分布的关系
- F分布构造,2个符合N(0,1) 标准正态分布得变量,和其自由度构造而成
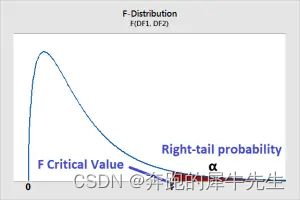
- F分布,本身是一个非对称,右偏非常明显得一个 类正态分布
- 所以,F分布,主要关注得是右尾的概率变化
4 什么是F分布
4.1 F分布的定义
4.1.1 维基百科的定义
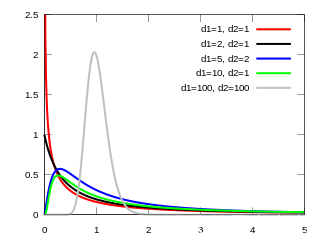
F分布是一种连续概率分布,
https://zh.wikipedia.org/wiki/F-%E5%88%86%E5%B8%83https://zh.wikipedia.org/wiki/F-%E5%88%86%E5%B8%83


4.1.2 来自百度百科的定义
- 可见,F分布用到的两个变量X1,X2 或者称X, Y
- 服从标准正态分布 N~(0,1)
- 也符合k2分布



4.3 检验的原理
- F检验临界值表提供了右尾F检验的临界值。
- 当F检验的统计量大于该值时,我们的F检验结果在统计上是有意义的。
- 也就是 显著度 α 和dfA 和 dfE 先确定了F分布曲线的形状
- 确定后,根据F值,在曲线上找到对应的曲线位置,下面围城的部分里右边部分面积就是p值=概率之和

4.4 F检验的实操(手工方法):根据dfA,dfE 和显著度α 查表得P值, 然后比较2个P值
4.4.1 显著度 α
- 实操一般选 0.05 0.01 等几个显著度α
4.4.2 自由度1=分子自由度=df1=dfA =自变量个数
- 自由度1
- 分子自由度
- df1
- dfA
- =自变量个数
4.4.3 自由度2=分母自由度=df2=dfE=n-k-1 = 样本总数- xi对应得参数ai个数- 截距1个参数
- 自由度2
- 分母自由度
- df2
- dfE
- =n-k-1 = 样本总数- xi对应得参数ai个数- 截距1个参数
4.4.4 总自由度,dfT=dfA+dfE
是回归模型的总自由度,需要加2者之和,暂时这里没啥用
4.4.5 用前面3个值来查表,获得查表的F值,然后比较2个F值
- 选择显著度 α,选择不同的表 →
- 选择自由度1=df1 →
- 自由度2=df2 →
- 查表得到F值 →
- 和计算的F值比较,如果大于查表的F,那么p肯定就小于了显著度α!要拒绝原假设。


4.5 F检验:计算机的方法,直接求得具体P值,再比较p和 α
- 直接根据 选择显著度 α,df1 ,df2 →
- 先计算出F值 →
- 然后计算出具体的P值 →
- 而不是我们查表的几个固定P值得边界,一般是 0.01,0.05 等
5 F统计量的几个公式分析对比
下面对比
5.1 F值构造的简单视角,便于理解
如果做了多次试验,现在得到多组数据,比如是两组
- 离差平方和∑(x-average(x))**2
- 样本标准偏差的平方=均方误差MS = S2=∑(x-average(x))**2/(n-1)
- 两组数据就能得到两个S2值F=S2/S2' (用较小的/较大的?)
- 然后计算的F值与查表得到的F表值比较,如果
- F < F表 表明两组数据没有显著差异;
- F ≥ F表 表明两组数据存在显著差异。
5.2 F=回归的均方差MS/ 残差的卷方差MS
- 在只存在一次试验,只得到一组样本时的计算F检验
- F=回归的均方差MS/ 残差的卷方差MS
5.2 F=组间波动/组内波动
- 如果是存在多次试验,有多种样本时的计算F检验
- F=组间波动/组内波动
- 因为只有多种样本,才存在多组样本之间的多样本二次平均均值,以及每组的均值,以及每组均值和多样本二次平均均值之间的差距,这就是所谓的组见波动
- 组内波动,当然就是组内数据的差异-离差,就是离差和离差的平方和。离差平方和除以自由度就是方差
- 神奇的是,当样本组数为1时,也就是不存在多组样本时,两者方法计算出来的F相等
- 而多次试验得到多组样本,应该只能按方法:F=组间波动/组内波动算
5.3 SSA/dfA的具体设计
5.3.1 这部分内容引用如下
方差分析:F检验 - 知乎方差分析主要是利用F检验来评估三组或更多组数据的均值情况。这篇文章主要聚焦以下问题: ① F统计量 ② F值 ③ F分布 ④ F检验 ⑥ 为何用方差分析来检验均值 在「六西格玛管理统计指南-Minitab使用指南」中,有这…![]() https://zhuanlan.zhihu.com/p/662096085
https://zhuanlan.zhihu.com/p/662096085
5.3.2 组间波动SSA 必须引入2个新参数:组间的组数k 和组内样本数量mi
- 也就是引入了2个新参数, 这2个都是样本组间和组内的重要信息,不能丢弃
- 1 样本组数,i=1~k
- 2 每个样本的数量大小m,mi


5.3.3 SSE组内波动必须引入2个新参数:组间的组数k 和组内样本数量mi
- 组内波动,只需要把每组的组内波动,再进行求和,二次求和就行了
- 但是也包含了,组间的k组数据信息,和组内的m个样本的信息

5.3.4 计算必须用MS,而不能直接用SS,或者SS的平方和
- 计算F值时,
- 还是要用均方差MS
- 而不能直接用 离差平方和!
5.3.5 SSA和SSE还要考虑df 自由度的影响
6 实操例子1:F值的计算

网图,只是拿来计算下具体F值
- df 自由度,自己看出来算下约束. 因子df=自变量数量,误差自由度=样本数n-约束,
- 整个模型自由度=两者相加
- SS,计算出来
- MS= 对应行的SS/DF
- F值=因子的ms/误差ms =回归的MS/ 残差的MS
这个F值的计算过程
- P值概率的由来,查表得到,有了F值,和 α 显著度可以查到P值
- 所以说F值本身不是判断标准,只是查表用的,关键还是p值
查表得到p
- 根据显著度α=0.05,df1=3,df2=16查表 p=3.24
- 而计算的p=7.95 显然大于3.24 查表值,也就意味着对应的p会小于显著度α=0.05,从而要拒绝原假设。
- 显著度α/p 其实就是p,都是概率值,显著度α只是一个特定刻度的概率p而已。
7 实操例子2 :详细的F值里SSA 和SSE 计算过程展开
7.1 题目来源
方差分析:F检验 - 知乎方差分析主要是利用F检验来评估三组或更多组数据的均值情况。这篇文章主要聚焦以下问题: ① F统计量 ② F值 ③ F分布 ④ F检验 ⑥ 为何用方差分析来检验均值 在「六西格玛管理统计指南-Minitab使用指南」中,有这…https://zhuanlan.zhihu.com/p/662096085![]() https://zhuanlan.zhihu.com/p/662096085
https://zhuanlan.zhihu.com/p/662096085

7.2 先计算SSE,这个只需要算每组样本内,每个X和对应均值的误差就可以

7.3 计算SSA,注意是组间的均值差异,只算均值和二次均值之间差异
- 均值:每组样本的均值
- 二次均值/组间均值= 所有样本均值的均值

7.4 计算自由度df

7.5 计算F值
因此 F值=(SSA/df1) / (SSE/ df2)

7.6 查表对比F值和查表F值
查表得到p
- 根据显著度α=0.05,df1=3,df2=16查表 p=3.24
- 而计算的p=7.95 显然大于3.24 查表值,也就意味着对应的p会小于显著度α=0.05,从而要拒绝原假设。
- 显著度α/p 其实就是p,都是概率值,显著度α只是一个特定刻度的概率p而已。
7.7 结论
拒绝原假设H0,两个分布x1 和x2的均值不相等。