一、直流电路

电路的组成
1. 电压和电流的参考方向
-
电压(Voltage):电压是电场力对电荷产生的作用,表示为电荷单位正电荷所具有的能量。在电路中,电压通常被定义为两点之间的电势差,具有方向性,沿着电场方向从高电势指向低电势,即电压降的方向。这个方向也被称为电压的极性。

-
电流(Current):电流是单位时间内电荷通过某一截面的量,通常用符号"i"表示。电流有方向,正电流表示电荷流动方向与某个参考方向相同,负电流表示电荷流动方向与参考方向相反
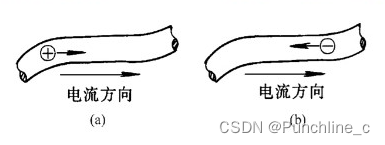
2. 电源的工作状态
- 电源:电源是提供电能供给电路或设备的装置。它可以是直流电源或交流电源。电源的工作状态通常分为工作状态和断开状态两种。在工作状态下,电源提供电流或电压给电路或设备;而在断开状态下,电源不提供电流或电压输出。
3. 欧姆定律
- 欧姆定律(Ohm’s Law):欧姆定律是电学基本定律之一,它表明电压、电流和电阻之间的关系。它的数学表达式为 V = I * R,其中 V 是电压(单位:伏特),I 是电流(单位:安培),R 是电阻(单位:欧姆)。该定律说明了在恒定温度下,电压与电流成正比,电压与电阻成正比,而电流与电阻成反比。

4. 基尔霍夫定律
- 基尔霍夫定律:基尔霍夫定律是描述电路中电压和电流分布的重要定律。
- 基尔霍夫第一定律(KCL)(节点定律):一个闭合电路中,任意一个节点处的入流电流等于出流电流的代数和。

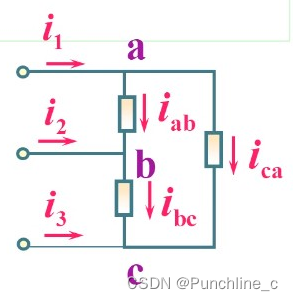
- 基尔霍夫第二定律(KVL)(环路定律):在任一瞬间,沿任一回路绕行方向,回路中各段电压的代数和恒等于0。
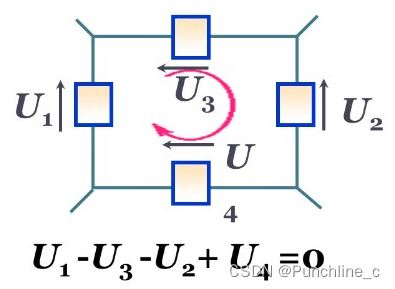
- 基尔霍夫第一定律(KCL)(节点定律):一个闭合电路中,任意一个节点处的入流电流等于出流电流的代数和。
5. 电位的概念及计算
-
电位:电位是指电荷在电场中由于所处位置的不同而具有的能量差异。在电路中,电位通常指电压,即某一点相对于某一参考点的电势差。电位的单位是伏特(V)。
-
电位的计算:电位差等于两点之间的电压。如果知道电压源的电压和电阻的电流,则可以使用欧姆定律计算两点之间的电压。另外,基尔霍夫定律也提供了一种计算电压的方法,特别是在复杂的电路中。
二、直流电路的分析方法
1. 等效变换
- 等效变换:在分析电路时,可以将复杂的电路元件或网络简化为等效的电路,以便更容易地进行分析和计算。例如,电阻网络可以用其等效电阻替换,电压源和电流源可以用其等效电压或电流替换。
- 示例:将若干电阻串联或并联后,用一个等效的电阻替代它们。例如,将两个串联的 10 欧姆电阻替换为一个 20 欧姆的等效电阻。
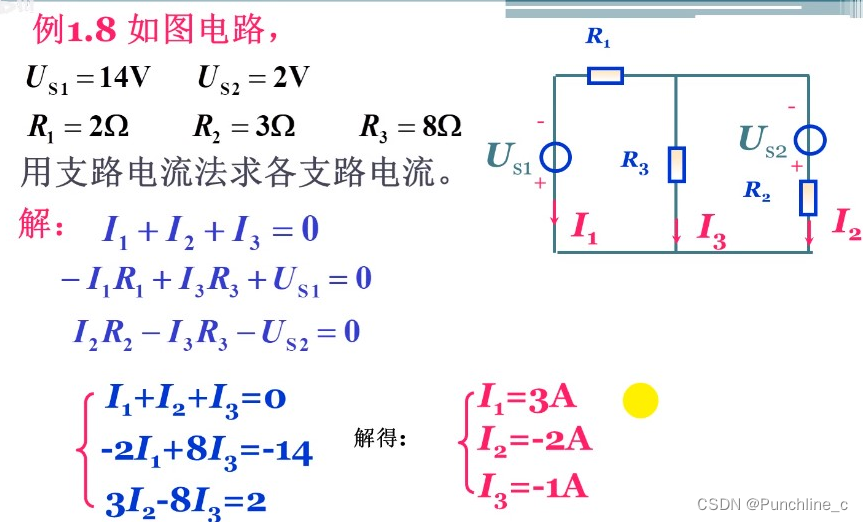
2. 支路电流法
- 支路电流法:支路电流法是一种基于电流的分析方法,它将电路中的各支路看作独立的电流来源,并根据基尔霍夫定律和欧姆定律建立支路电流方程组,从而求解电路中各支路的电流。
- 示例:考虑一个简单的电路,其中有两个并联的电阻和一个串联的电压源。使用支路电流法,可以将电路中的电流流向每个支路,并根据欧姆定律和基尔霍夫定律列出方程组,进而求解电路中的电流。
3. 叠加定理
- 叠加定理:叠加定理适用于线性电路,它指出复杂电路中的任意一个响应可以分解为各个独立电源作用下的单个响应之和。因此,可以分别考虑每个电源对电路的影响,然后将它们叠加起来得到最终结果。
- 示例:考虑一个电路中有两个电压源,分别为 5 伏特和 10 伏特,与一个串联的电阻。使用叠加定理,可以分别计算每个电压源作用下的电流,然后将它们相加以得到电路中的总电流。
 注:功率不可叠加(P=I^2*R)
注:功率不可叠加(P=I^2*R)
4. 戴维宁定理
- 戴维宁定理:戴维宁定理是一种基于等效变换的分析方法,它将电路中的电压源和电流源分别替换为其内部电阻的等效电路,从而简化电路结构,便于分析。
- 示例:考虑一个电路中有一个电压源和一个电流源,与一些电阻串联并并联。使用戴维宁定理,可以将电压源和电流源替换为其内部电阻的等效电路,从而简化整个电路,便于分析。
5. 结点电压法
- 结点电压法:结点电压法是一种基于电压的分析方法,它将电路中的每个节点的电压作为未知数,根据基尔霍夫定律和欧姆定律建立节点电压方程组,从而求解电路中各节点的电压。