📖 敌兵布阵
C国的死对头A国这段时间正在进行军事演习,所以C国间谍头子Derek和他手下Tidy又开始忙乎了。A国在海岸线沿直线布置了N个工兵营地,Derek和Tidy的任务就是要监视这些工兵营地的活动情况。由于采取了某种先进的监测手段,所以每个工兵营地的人数C国都掌握的一清二楚,每个工兵营地的人数都有可能发生变动,可能增加或减少若干人手,但这些都逃不过C国的监视。
中央情报局要研究敌人究竟演习什么战术,所以Tidy要随时向Derek汇报某一段连续的工兵营地一共有多少人,例如Derek问:“Tidy,马上汇报第3个营地到第10个营地共有多少人!”Tidy就要马上开始计算这一段的总人数并汇报。但敌兵营地的人数经常变动,而Derek每次询问的段都不一样,所以Tidy不得不每次都一个一个营地的去数,很快就精疲力尽了,Derek对Tidy的计算速度越来越不满:"你个死肥仔,算得这么慢,我炒你鱿鱼!”Tidy想:“你自己来算算看,这可真是一项累人的工作!我恨不得你炒我鱿鱼呢!”无奈之下,Tidy只好打电话向计算机专家Windbreaker求救,Windbreaker说:“死肥仔,叫你平时做多点acm题和看多点算法书,现在尝到苦果了吧!”Tidy说:"我知错了。。。"但Windbreaker已经挂掉电话了。Tidy很苦恼,这么算他真的会崩溃的,聪明的读者,你能写个程序帮他完成这项工作吗?不过如果你的程序效率不够高的话,Tidy还是会受到Derek的责骂的.
输入
第一行一个整数T,表示有T组数据。
每组数据第一行一个正整数N(N<=50000),表示敌人有N个工兵营地,接下来有N个正整数,第 i 个正整数
a
i
a_i
ai 代表第i个工兵营地里开始时有
a
i
a_i
ai 个人(
1
<
=
a
i
<
=
50
1<=a_i<=50
1<=ai<=50)。
接下来每行有一条命令,命令有4种形式:
- Add i j,i和j为正整数,表示第 i 个营地增加 j 个人(j不超过30)
- Sub i j,i和j为正整数,表示第 i 个营地减少 j 个人(j不超过30);
- Query i j,i和j为正整数,i<=j,表示询问第i到第 j 个营地的总人数;
- End 表示结束,这条命令在每组数据最后出现;
每组数据最多有40000条命令
输出
对第i组数据,首先输出“Case i:”和回车,
对于每个Query询问,输出一个整数并回车,表示询问的段中的总人数,这个数保持在int以内。
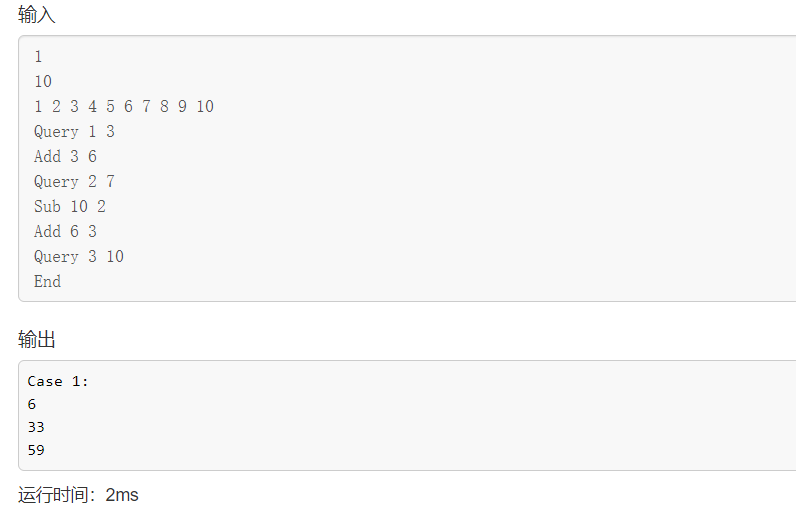
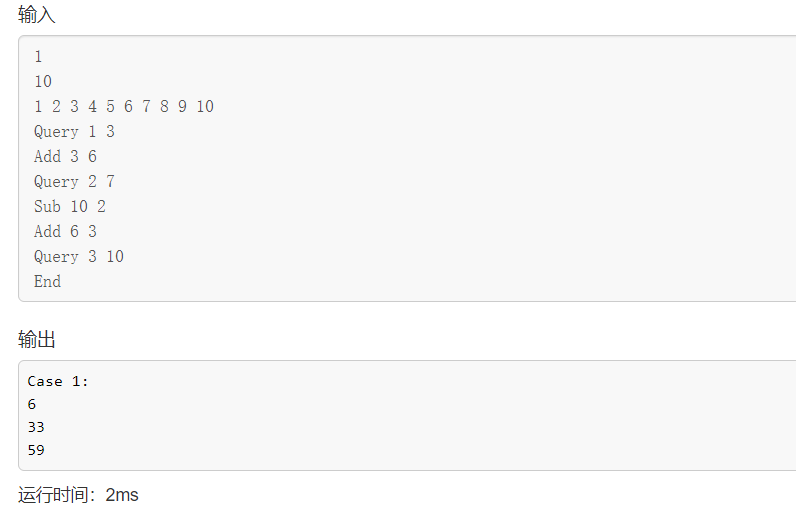
⌨ 输入样例
1
10
1 2 3 4 5 6 7 8 9 10
Query 1 3
Add 3 6
Query 2 7
Sub 10 2
Add 6 3
Query 3 10
End
💻 输出样例
Case 1:
6
33
59
👨🏫 参考地址
💖 线段树版

🌟 Main.java
import java.util.Scanner;
class SegmentTree
{
// 定义内部类 Node,表示线段树的节点
class Node
{
int l, r, sum;// 区间为 [l,r],区间和为 sum
// Node 类的构造函数,用于初始化节点的起始和结束位置以及和
Node(int a, int b)
{
this.l = a;
this.r = b;
this.sum = 0;
}
}
// 数组存树,tree[i] 的左儿子为 tree[2i],右儿子为 tree[2i+1]
Node[] tree; // 线段树数组,存储线段树的节点
int[] workers; // 工兵营地人数数组,存储每个工兵营地的人数
// SegmentTree 类的构造函数,初始化线段树和工兵营地人数数组
SegmentTree(int n)
{
tree = new Node[4 * n]; // 线段树数组的大小是工兵营地数量的 4 倍
workers = new int[n + 1]; // 工兵营地人数数组的大小是工兵营地数量加一
}
// 构造线段树的方法
/**
* @param l 区间左边界
* @param r 区间右边界
* @param cur 当前区间的根节点
*/
void build(int l, int r, int cur)
{
tree[cur] = new Node(l, r); // 初始化线段树的节点
// 如果起始位置和结束位置相同,表示到达叶子节点,将叶子节点的和设置为对应工兵营地的人数
if (l == r)
tree[cur].sum = workers[l];
else
{
// 如果不是叶子节点,则递归构造左右子树,并将当前节点的和设置为左右子树和的和
int mid = (l + r) / 2;
build(l, mid, cur * 2);
build(mid + 1, r, cur * 2 + 1);
tree[cur].sum = tree[cur * 2].sum + tree[cur * 2 + 1].sum;
}
}
// 查询线段树中指定闭区间 [l,r] 的和
/**
* @param l 区间左边界
* @param r 区间右边界
* @param cur 当前区间的根节点
*/
int query(int l, int r, int cur)
{
int sum = 0;
// 如果查询范围包含了当前节点的范围,则返回当前节点的和
if (l <= tree[cur].l && r >= tree[cur].r)
sum += tree[cur].sum;
else
{
int mid = (tree[cur].l + tree[cur].r) / 2;
// 否则根据查询范围的位置递归查询左右子树
if (l > mid)// 查询的区间 和 左区间 没有交集
sum += query(l, r, cur * 2 + 1);
else if (r <= mid)// 查询的区间 和 右区间 没有交集
sum += query(l, r, cur * 2);
else// 和左右区间都有交集
{
sum += query(l, r, cur * 2);
sum += query(l, r, cur * 2 + 1);
}
}
return sum;
}
// 在线段树中指定位置增加值
/**
* 单点修改:给 tree[idx].sum 加上 val 值
*
* @param idx 要修改的值下标
* @param val 增加多少
* @param cur 当前节点
*/
void add(int idx, int val, int cur)
{
tree[cur].sum += val;// 子结点变动,父结点肯定得变动
// 如果当前节点的范围等于要增加值的位置,则直接返回
if (tree[cur].l == idx && tree[cur].r == idx)
return;
// 否则根据要增加值的位置递归更新左右子树
if (idx > (tree[cur].l + tree[cur].r) / 2)
add(idx, val, cur * 2 + 1);
else
add(idx, val, cur * 2);
}
}
public class Main
{
public static void main(String[] args)
{
Scanner sc = new Scanner(System.in);
int cnt = 0;
int t = sc.nextInt(); // 读取测试用例数量
while (t-- > 0)
{
int n = sc.nextInt(); // 读取工兵营地数量
SegmentTree segmentTree = new SegmentTree(n); // 创建线段树实例
segmentTree.workers[0] = 0;
for (int i = 1; i <= n; i++)
segmentTree.workers[i] = sc.nextInt(); // 读取每个工兵营地的人数
segmentTree.build(1, n, 1); // 构造线段树
System.out.println("Case " + ++cnt + ":");
while (true)
{
String ch = sc.next(); // 读取操作类型
if (ch.equals("End"))
break;
else if (ch.equals("Query"))
{
int l = sc.nextInt(); // 读取查询范围起始位置
int r = sc.nextInt(); // 读取查询范围结束位置
int sum = segmentTree.query(l, r, 1); // 查询线段树中指定范围的和
System.out.println(sum); // 输出查询结果
} else if (ch.equals("Add"))
{
int idx = sc.nextInt(); // 读取要增加值的位置
int x = sc.nextInt(); // 读取要增加的值
segmentTree.add(idx, x, 1); // 在线段树中指定位置增加值
} else if (ch.equals("Sub"))
{
int idx = sc.nextInt(); // 读取要减少值的位置
int x = sc.nextInt(); // 读取要减少的值
segmentTree.add(idx, -x, 1); // 在线段树中指定位置减少值
}
}
}
}
}
运行结果

🌟 Cpp
Cpp代码全文摘抄
#include<iostream>
#include<cstring>
#include<cstdio>
using namespace std;
struct
{
int a,b,sum;
}t[140000];
int r[50010],summ,k;
void buildd(int x,int y,int num)//构造线段树
{
t[num].a=x;
t[num].b=y;
if(x==y)
t[num].sum=r[y];
else
{
buildd(x,(x+y)/2,num*2);
buildd((x+y)/2+1,y,num*2+1);
t[num].sum=t[num*2].sum+t[num*2+1].sum;
}
}
void query(int x, int y, int num)//查找
{
if(x<=t[num].a&&y>=t[num].b)
summ+=t[num].sum;
else{
int minn=(t[num].a+t[num].b)/2;
if(x>minn) query(x,y,num*2+1);
else if(y<=minn)
query(x,y,num*2);
else
{
query(x,y,num*2);
query(x,y,num*2+1);
}
}
}
void add(int x, int y, int num)//添加
{
t[num].sum+=y;
if(t[num].a==x&&t[num].b==x) return ;
if (x>(t[num].a+t[num].b)/2) add(x,y,num*2+1);
else add(x,y,num*2);
}
void sub(int x,int y,int num)//减少
{
t[num].sum-=y;
if(t[num].a==x&&t[num].b==x) return ;
if(x>(t[num].a+t[num].b)/2) sub(x,y,num*2+1);
else sub(x,y,num*2);
}
int main()
{
int t;
int cnt=0;
scanf("%d",&t);
while(t--)
{
int n,m;
char ch[10];
scanf("%d",&k);
r[0]=0;
for(int i=1;i<=k;i++)
scanf("%d",&r[i]);
buildd(1,k,1);
printf("Case %d:\n",++cnt);
while(scanf("%s",&ch))
{
if(strcmp(ch,"End")==0)
break;
else if(strcmp(ch,"Query")==0)
{
scanf("%d%d",&n,&m);
summ=0;
query(n,m,1);
printf("%d\n",summ);
}
else if(strcmp(ch,"Add")==0)
{
scanf("%d%d",&n,&m);
add(n,m,1);
}
else if(strcmp(ch,"Sub")==0)
{
scanf("%d%d",&n,&m);
sub(n,m,1);
}
}
}
return 0;
}
测试结果
💖 离散数组版
🌟 Main.java
import java.util.Scanner;
public class Main
{
static int[] numbers = new int[500050]; // 存储输入的数据
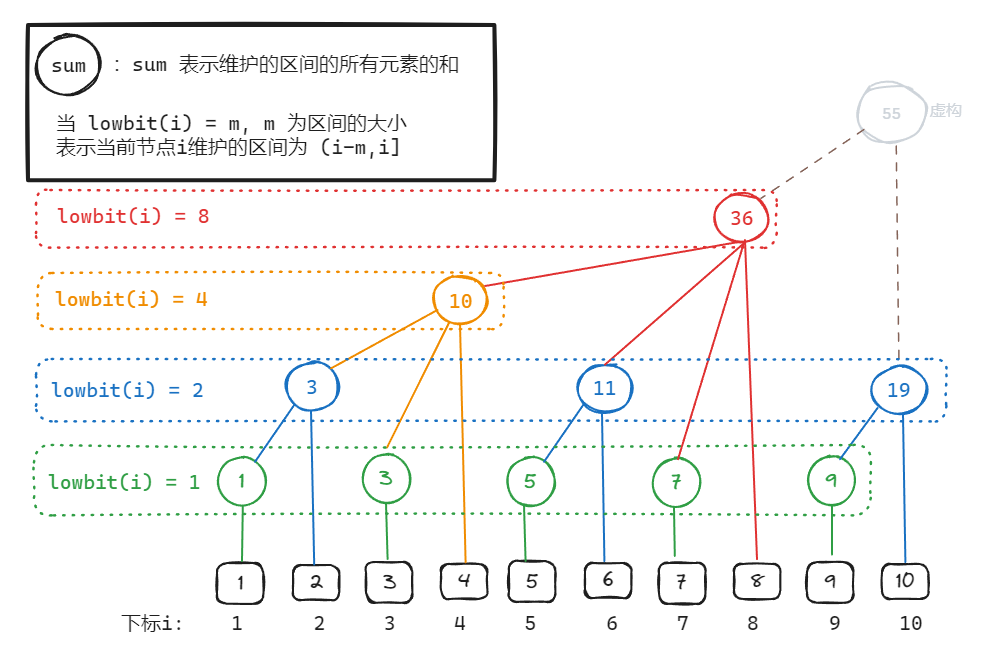
// prefixSum[i] 表示numbers区间(i-lowbit(i),i] 区间的所有数的和
static int[] prefixSum = new int[500050]; // 存储树状数组的前缀和
// 计算二进制中最低位1的位置,树状数组的核心函数
static int lowbit(int x)
{
// 假设 x = 12
// 补码: 0000 1100 目测lowbit(12) = 100(二进制) = 4
// 取反: 1111 0011 所有位都取反
// 取反+1:1111 0100
// lowbit(x) = x补码 & (x补码取反+1) = 0000 0100
//
// 假设 y = -12
// 原码:1000 1100 (假设只有 8 位)
// 反码:1111 0011
// 补码:1111 0100 巧了:y的补码==x的补码取反加一
//
// 结论:lowbit(x) = x & (-x)
return x & (-x);
}
// 建立树状数组
static void buildPrefixSum(int n)
{
// 后面的节点只会依赖于前边的节点,所以从前往后更新
for (int i = 1; i <= n; i++)
{ // 遍历数组,计算树状数组的前缀和
for (int j = i; j >= i - lowbit(i) + 1; j--) // 累加区间 (i-lowbit(i),i] 的值
prefixSum[i] += numbers[j];
}
}
// 计算前n个元素的前缀和
static int calculatePrefixSum(int n)
{
int sum = 0;
// 累计 n~1 所有值的和, 分区间累加即可
// (n-lowbit(n),n],[ 某,n-lowbit(n)] ……
// 可见区间的步长为 当前区间的长度 lowbit(i)
for (int i = n; i > 0; i -= lowbit(i))
sum += prefixSum[i];
return sum;
}
// 更新树状数组
static void updatePrefixSum(int index, int value, int n)
{
for (int i = index; i <= n; i += lowbit(i)) // 按照lowbit规则,更新前缀和数组
prefixSum[i] += value;
}
public static void main(String[] args)
{
Scanner sc = new Scanner(System.in); // 创建Scanner对象,用于读取输入
int testCaseCount = sc.nextInt(); // 读取测试用例的数量
int caseNumber = 1; // 记录当前测试用例的编号
while (testCaseCount-- > 0)
{ // 处理每个测试用例
int length = sc.nextInt(); // 读取数组长度
for (int i = 1; i <= length; i++)
{ // 读取数组元素
numbers[i] = sc.nextInt();
}
buildPrefixSum(length); // 建立树状数组
System.out.println("Case " + caseNumber++ + ":"); // 打印测试用例编号
while (sc.hasNext())
{ // 处理每个操作
String operation = sc.next(); // 读取操作类型
if (operation.equals("End")) // 如果操作类型为End,退出循环
break;
int start, end;
start = sc.nextInt(); // 读取操作参数
end = sc.nextInt();
if (operation.equals("Query")) // 如果操作类型为Query,打印查询结果
System.out.println(calculatePrefixSum(end) - calculatePrefixSum(start - 1));
else if (operation.equals("Add")) // 如果操作类型为Add,更新树状数组
updatePrefixSum(start, end, length);
else if (operation.equals("Sub")) // 如果操作类型为Sub,更新树状数组
updatePrefixSum(start, -1 * end, length);
}
}
sc.close(); // 关闭Scanner对象
}
}
🌟 Cpp
#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
using namespace std;
int a[500050];
int summ[500050];
int low(int x)//lowbit 函数,树状数组的核心
{
return x&(-x);
}
void build(int n)//建立树状数组
{
for(int i=1;i<=n;i++)
{
for(int j=i;j>=i-low(i)+1;j--)
summ[i]+=a[j];
}
}
int s_sum(int n)//求n前的和
{
int sum=0;
for(int i=n;i>0;i-=low(i))
sum+=summ[i];
return sum;
}
void update(int x,int y,int n)//对树状数组进行修改
{
for(int i=x;i<=n;i+=low(i))
summ[i]+=y;
}
int main()
{
int t,k,num=1;
scanf("%d",&t);
while(t--)
{
scanf("%d",&k);
memset(a,0,sizeof(a));
memset(summ,0,sizeof(summ));
for(int i=1;i<=k;i++)
scanf("%d",&a[i]);
build(k);
char x[10];
int a,b;
printf("Case %d:\n",num++);
while(scanf("%s",x))
{
if(strcmp(x,"End")==0)
break;
scanf("%d%d",&a,&b);
if(strcmp(x,"Query")==0)
printf("%d\n",s_sum(b)-s_sum(a-1));
else if(strcmp(x,"Add")==0)
update(a,b,k);
else if(strcmp(x,"Sub")==0)
update(a,-1*b,k);
}
}
return 0;
}
测试结果