1. LC 3102 最小化曼哈顿距离
VP周赛391 T4。这是个结论题目。
首先曼哈顿距离是需要两个数对而不是两个数去进行比较的,两个数之间你很轻易就知道差的绝对值最大是多少了,只要挑最大和最小两个数一减就可以了。
但是两个数对之间各项差的绝对值之和最大是多少就不好说了。假设第一个数对的第一项是所有第一项里最大的,第二个数对的第一项是所有第一项里最小的,他俩之间的曼哈顿距离不一定是最大的。所以就很难比。
这就引入了切比雪夫距离。
refs(from 0x3f的题解):
<https://leetcode.cn/problems/minimize-manhattan-distances/solutions/2716755/tu-jie-man-ha-dun-ju-chi-heng-deng-shi-b-op84>
将整个坐标系顺时针旋转45°,然后扩大根号二倍,则原坐标系上任意一点(x,y)的坐标变为(x’,y’)=(x+y,y-x)。
推导过程如下:
假设旋转矩阵为R
假设扩大矩阵为S
则transpose(x',y') = SR*transpose(x,y)
旋转矩阵:
1. 对于点(1,0),顺时针旋转45°,变成了(1/sqrt(2),-1/sqrt(2))
2. 对于点(0,1),顺时针旋转45°,变成了(1/sqrt(2),1/sqrt(2))
所以旋转矩阵为
[
[ 1/sqrt(2),1/sqrt(2) ]
[ -1/sqrt(2),1/sqrt(2) ]
]
扩大矩阵:
1. 对于点(1,0),扩大根号二倍,变成了(sqrt(2),0)
2. 对于点(0,1),扩大根号二倍,变成了(0,sqrt(2))
所以扩大矩阵为
[
[ sqrt(2),0 ]
[ 0,sqrt(2) ]
]
这样SR为
[
[ 1,1 ]
[-1,1 ]
]
所以(x',y') = (x+y,-x+y)
当我们把操作后的坐标投影到原先坐标系的x轴或y轴上后,原先两个点之间的距离,就变成了投影在x/y轴上的距离,这是因为投影把线段缩小到原来的1/sqrt(2)倍,正好和扩大sqrt(2)倍兑掉了。
如下图,红色线段是欧式距离,深蓝色线段是曼哈顿距离,灰色射线是新坐标系x轴和y轴,黑色射线是原坐标系x轴和y轴,橙色线段是切比雪夫距离,就等于原坐标系的曼哈顿距离,也就是橙色线段的长度等于左边图中两条深蓝色线段的长度。
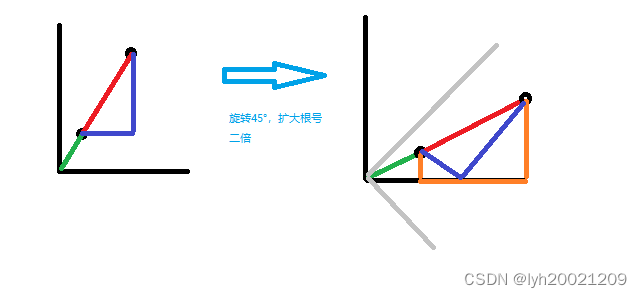
这样就做了一个很nb的事情,我们把原先二维点对的距离给降维了,变成一维的了,这样就能选一个最大值,选一个最小值,然后相减得到最大的绝对值。
需要注意的是,有时候投影完的距离会是原先两个折线长度的差而不是和,比如上图中如果投影到y会发现切比雪夫距离是2-1=1而不是3。解决这个问题的方式就是我们把投影到x和投影到y轴上的两个线段的长度取一个较大值,这样就是切比雪夫距离了。
java没有sortedList,所以可以TreeMap来维护,一个专门用来存新坐标系下的x坐标,一个存新坐标系下的y的坐标。然后枚举被删除的,从剩下的里面挑一个最大的,一个最小的,相减,更新答案。记得最大最小都要各自选x和y,然后相减完取个较大值作为切比雪夫距离。
import java.util.TreeMap;
class Solution {
public int minimumDistance(int[][] points) {
TreeMap<Integer, Integer> xs = new TreeMap<>();
TreeMap<Integer, Integer> ys = new TreeMap<>();
for (int[] point : points) {
int x = point[0];
int y = point[1];
xs.merge(x+y,1,Integer::sum);
ys.merge(y-x,1,Integer::sum);
}
int ans = Integer.MAX_VALUE;
for (int[] point : points) {
int x = point[0];
int y = point[1];
int x_ = x + y;
int y_ = y - x;
if(xs.get(x_)==1){
xs.remove(x_);
}else{
xs.merge(x_,-1,Integer::sum);
}
if(ys.get(y_)==1){
ys.remove(y_);
}else{
ys.merge(y_,-1,Integer::sum);
}
ans = Math.min(ans,Math.max(
xs.lastKey()-xs.firstKey(),ys.lastKey()-ys.firstKey()
));
xs.merge(x_,1,Integer::sum);
ys.merge(y_,1,Integer::sum);
}
return ans;
}
}