🌱 博主简介: 是瑶瑶子啦 ,一名大一计科生,目前在努力学习C进阶、数据结构、算法、JavaSE。热爱写博客~正在努力成为一个厉害的开发程序媛!
📜 所属专栏: C语言
✈ 往期博文回顾: 【Java基础篇】Java重要特性,JDK,JRE,JVM区别和联系,环境变量
🕵️♂️ 近期目标:成为百粉小博主。持续输出JavaSE、C进阶、数据结构、算法相关的优质博客,
🙇♀️ 写博客理念:力求用自己的语言加上自己的理解去阐述知识知识、技术(费曼学习法)。喜欢画图、思维导图去描述过程和知识之间的联系。
🎊 工具:思维导图:Xmind;关系图,流程图: diagrams.net
🎡 您的 点赞 、 关注 、 收藏 、 评论 ,是对我最大的激励和支持!!!
🌺 :“再牛的程序员也是从小白开始,既然开始了,就全身心投入去学习技术”
数据类型存在的意义
我们知道,变量的创建是要在内存中申请空间的,那你用编程语言和计算机沟通的时候,你就要告诉计算机你要申请多大的空间,那么就需要在变量名前放一个数据类型,告诉计算机:我要给这个变量开辟这个类型所对应的这么大内存空间.简而言之,数据类型决定了变量所占空间的大小.
确定了变量空间还不够,因为我们知道,对数据进行操作,首先我们也要知道它是浮点型?字符型?数组?因为不同的属性有不同的操作,计算机进行操作,更应该有这方面的知晓权.所以,数据类型决定了计算机看待该片内存中数据的视角.(认为是浮点型呀,还是字符型?)
C语言整形家族:
char---字符类型在内存中以其Ascii码表对应数值存储
signed char
unsigned char
char :默认具体是signed还是unsigned具体看编译器,常见是signed
short
signed short [int](默认)
unsigned short [int]
int
signed int(默认)
unsigned int
long
signed long [int](默认)
unsigned long [int]
🎉下面是Linux的64位操作系统下给出的,在不同操作系统下可能有所不同,在使用的时候应该测试之后再使用:使用sizeof(类型名)测试
类型 | 类型关键字 | 字节数 | (二进制)位数 | 表示范围 |
字符型 | (signed) char | 1 | 8(1*8) | -128~127 |
无符号字符型 | unsigned char | 1 | 8 | 0~255 |
短整形 | (signed) short (int) | 2 | 16 | -32768~32767(-2^15~2^15-1) |
无符号短整形 | unsigned short (int) | 4 | 16 | 0~65535(0~2^16-1) |
整形 | (signed) int | 4 | 32 | -2147483648~2147483647(-2^31~2^31-1) |
无符号整形 | unsigned int | 4 | 32 | 0~4294967295(0~2^32-1) |
长整型 | (signed) long (int) | 8 | 64 | 2^63~2^63-1 |
无符号长整形 | unsigned long (int) | 8 | 64 | 0~2^64-1 |
C语言浮点型家族
类型名称 | 类型关键字 | 字节数 | 位数 | 有效数字 |
单精度浮点数 | float | 4 | 32 | 7位有效数字 |
双精度浮点数 | double | 8 | 64 | 15~16位有效数字 |
C语言中构造类型(自定义类型)
数组
结构体--struct
枚举--enum
联合--union
整形在内存中的存储:
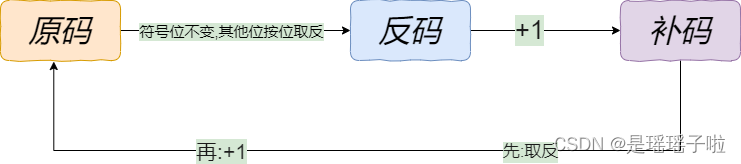
计算机中的整数有3种表示方式(用二进制): 原码(true form),反码,补码.
✨ 原码:就是十进制直接转换成二进制所得到的二进制序列
每一种表达方式,都有: 符号位,数值位之分
符号位(最高位) | |
正数 | 0 |
负数 | 1 |
正数的源码,反码,补码均相同!!!
负整数的三种表达方式都不相同(需要经过相应的转换)
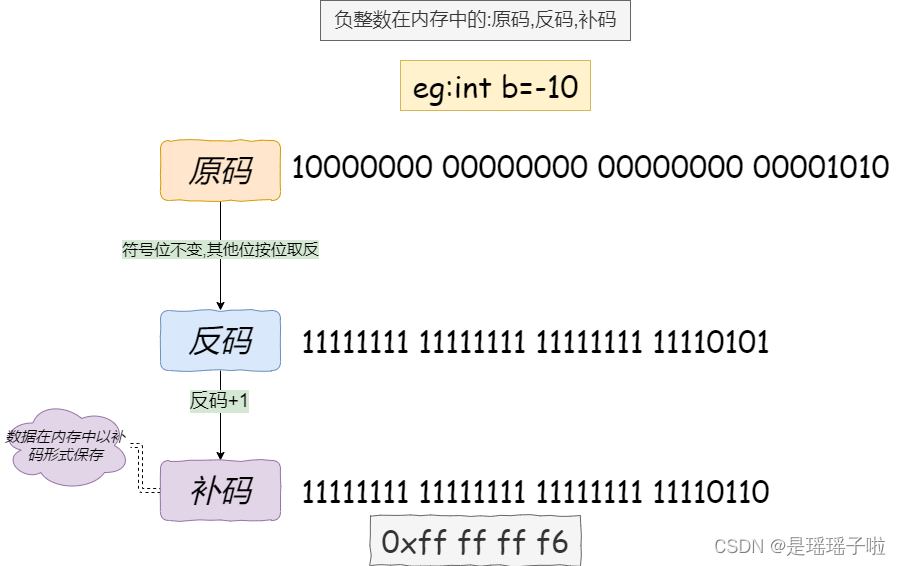
原码,补码,反码,为什么存在?
我们可能会想,为什么要设计出来3个东东,像我们自己平时10进制计算,都是直接进行的呀,没有说这么复杂.为什么不直接都用原码来表示呢?
十进制和二进制有很大不同,10进制有专门的一个符号来表示正负,而且我们要站在机器的思路去思考.因为机器语言只认识:0和1
而且,CPU只有加法器哦,比如1-1会被转换为1+(-1)
🎉假如整数在内存中也用原码来表示?
1: 00000000 00000000 00000000 00000001//原码
-1:10000000 00000000 00000000 00000001//负数原码
//相加:
10000000 00000000 00000000 00000010//-2 ???由此可知,用原码,是不可能算出正确结果的
🎃原反补存在意义:
使正数和负整数能够正确进行运算,并得到正确结果
统一处理符号位和数值位:在计算的时候不用特别去对待符号位
统一处理加法\减法
而且,原->反->补和补->反->原所执行的流程是一样的,不需要额外的硬件电路.
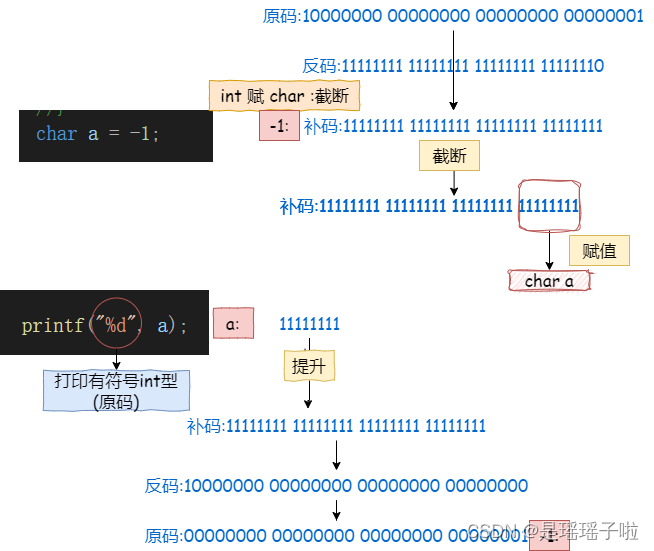
char a = -1;
unsigned char b = -1;
printf("%d %d", a, b);
// -1 255执行过程分析:(一定要注意的点)
截断赋值
整形提升
操作补码(内存中对整数的操作:无论是赋值\加减\截断,都是对补码进行操作)
原码显示(简单理解为,从内存中取出数据,来打印数据,看看值是多少的时候,取出的原码哦)
注意:内存中对数据的一些操作,都是在补码上进行的.要show这个数据((比如以%d形式打印)是多少的时候,才用到原码.
补充:C语言格式控制字符使用说明:(用格式字符来打印的时候,不同的格式字符,体现了取出数据来展示的时候,看待补码的不同视角)
字符 | 含义 |
%d | 十进制有符号整数(signed int) |
%o | 八进制无符号整数 |
%x | 十六进制无符号整数 |
%u | 十进制无符号整数(unsigned int) |
%c | 单个字符 |
%s | 字符串 |
%e | 指数形式浮点数 |
%f | 小数形式单精度浮点数 |
%g | 取e和f中较短的一种格式 |
%% | 百分号本身 |
%lf | 小数形式双精度浮点数 |
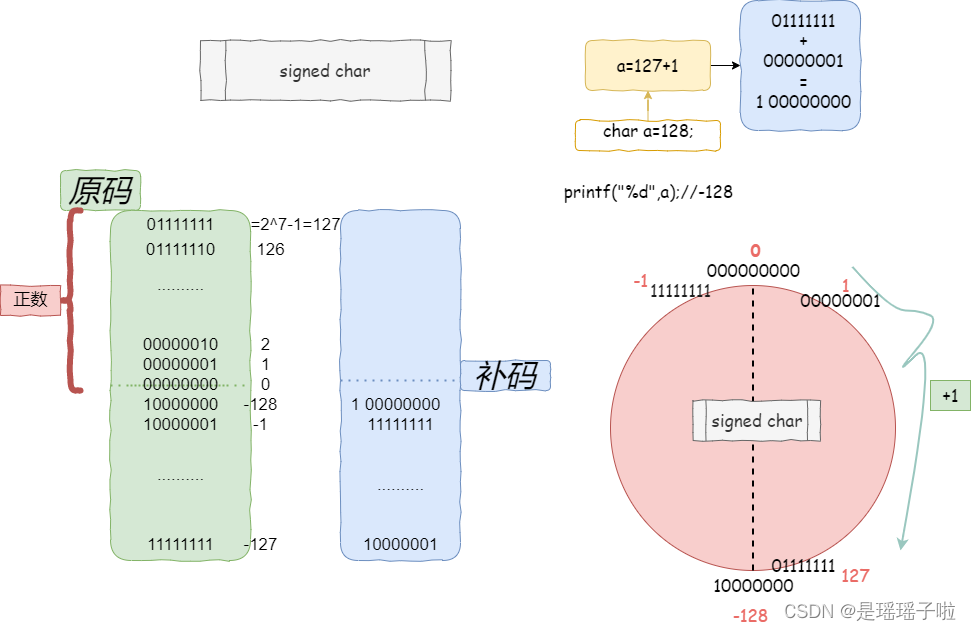
对取值范围的进一步思考:
设计得真的很神奇,数据的类型,限定死了范围,范围是个"闭环",或者是"周期函数".无论如何都出不了这个范围(长度规定和截断的功劳🐣)
通过一道题来真实感受一下:
这段代码的输出结果是???
说实话我一开始认为是:3,2,1,0
运行之后才发现,太天真了,太天真了!!!
#include<stdio.h>
int main() {
unsigned int i = 0;
for (i = 3; i >= 0; i--) {
printf("%d", i);
}
return 0;
}要注意的是:i被范围限定死了,无符号(0~2^32-1),也就是说, 无论怎么对i进行操作,i>=0是恒成立的呀!!所以是个死循环!
再者需要注意的是,%d决定了取出数据时看待内存的视角("我就认为你是signed int")
大,小端字节序存储
注意,这里的存储顺序,是以字节为单位!!!(即8bits)
大小端字节序介绍:
大端字节序存储:高数值位的数据存在低地址处,低数值位的数据存在低地址出(按顺序)
小端字节序存储:低数值位的数据存在高地址处,高数值位的数据存在低地址处(按顺序)

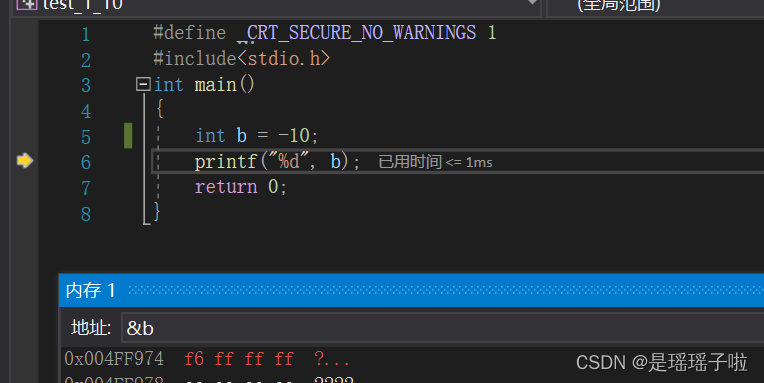
可以看到vs2019是采用小端存储的
为什么会存在大,小端字节序存储?
一个超过一个字节的要在内存中存储,如何安排这几个字节在内存中存储的顺序?安排好顺序后应该考虑如何尽可能方便的将数据取出病还原数据.通过排序可知,将不同的字节数据安排位置在内存中存储可谓有无数中方法.为了尽可能简便的存储数据,更是为了尽可能方便的取出数据,最终就这保留了两种字节顺序存储的方法.
笔试题:写一端程序来判断当前机器是大端存储还是小端存储
//写一个程序来判断当前机器是大端存储还是小端存储
int a = 1;//0x00 00 00 01
char* p = (char*)(&a);
if ((*p) == 1) {
printf("小端");
}
else {
printf("大端");
}
return 0;🛸key;利用了指针的类型决定了指向空间的大小
浮点数在内存中的存储
🎀这一小节,我们要解决的问题是:
浮点数在内存中如何存储
浮点数存储和取出的流程
为什么之前总是提到浮点数的精度,浮点数表示不准确?
浮点数在内存中如何存储
根据IEEE(电气电子工程师学会)规定, 在内存中,任何一个二进制的浮点数,可以表示为一下形式:
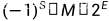
:表示浮点数的正负
: 有效数字(1<=M<2)( 1+小数点后的位数=有效数字位数)
:指数位
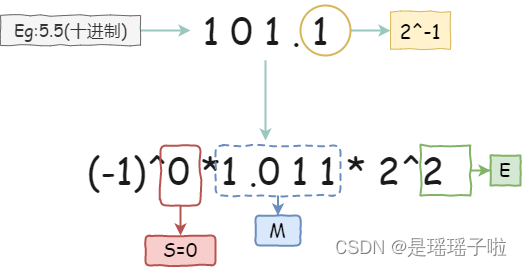
🌌思考:通过例子我们可以知道,只要S,M,E三个变量确定了,那么这个浮点数也就确定了,所以我们只需要把S,M,E在内存中存储起来即可.
能用图形解释清楚就不用文字了~
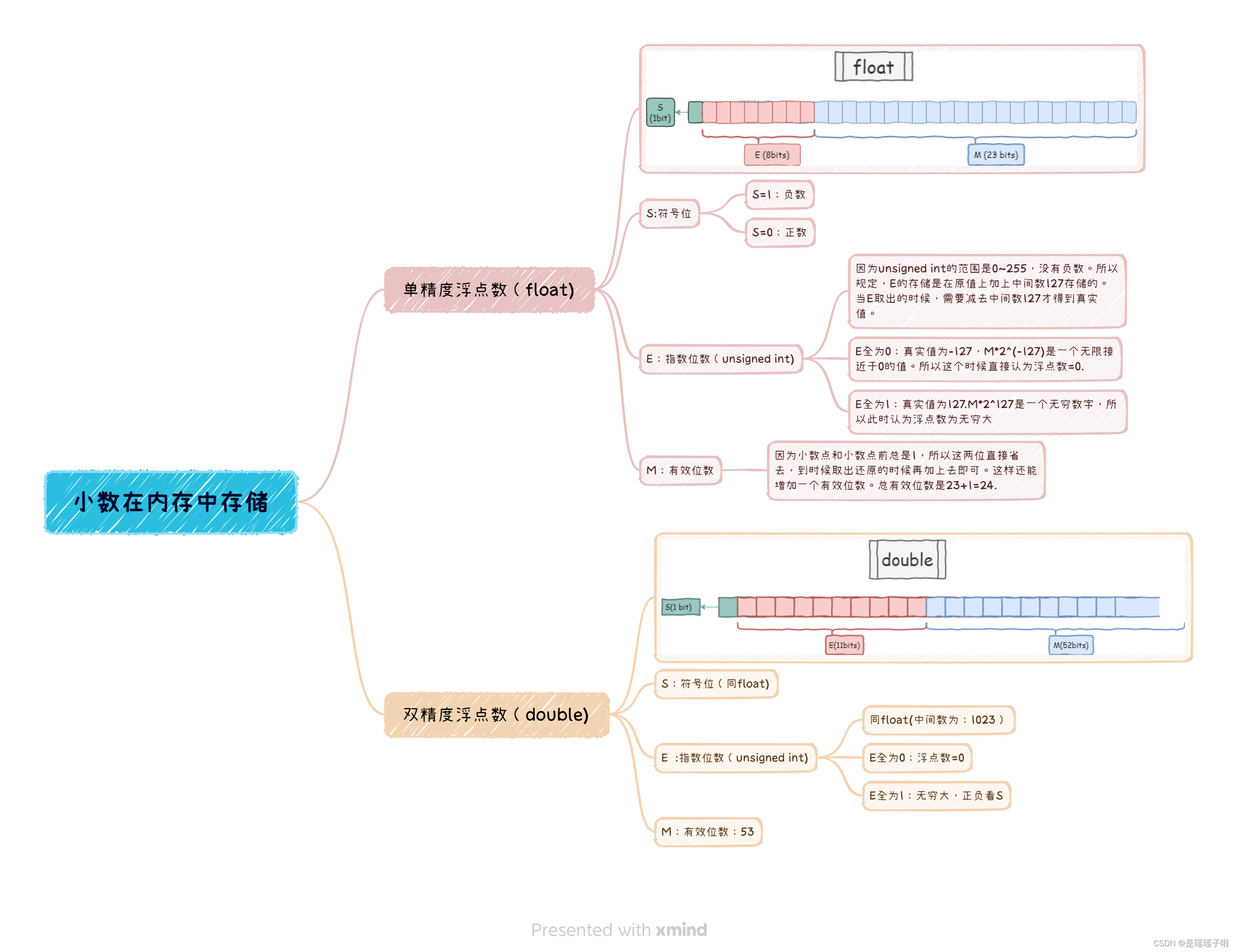
浮点数取出和存储的流程:
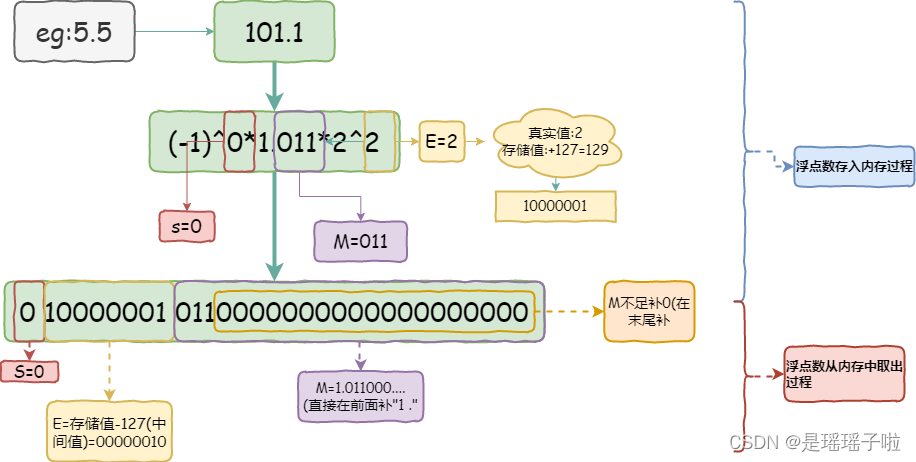
深入思考:为什么浮点数的储存不准确?
我们知道,十进制浮点数转换为二进制浮点数,小数点后的十进制表示也要转换成二进制表示形式.
eg:5.5
101.1
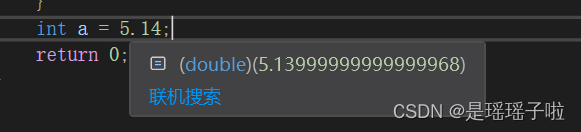
eg:5.14
101.00101...........可以看到,关键是: 无法用二进制准确表达出小数点后的数字,此时只能无限接近,不精确.
🎉 这就是数据在内存中储存的全部内容了,码文,作图不易,如果对你有帮助,您的关注 ❤ 点赞 👍 收藏 ⭐ 评论 🌻 是对我最大激励!
![[JAVA安全]CVE-2022-33980命令执行漏洞分析](https://img-blog.csdnimg.cn/ca2467f0031a447790cad860009d0190.png)