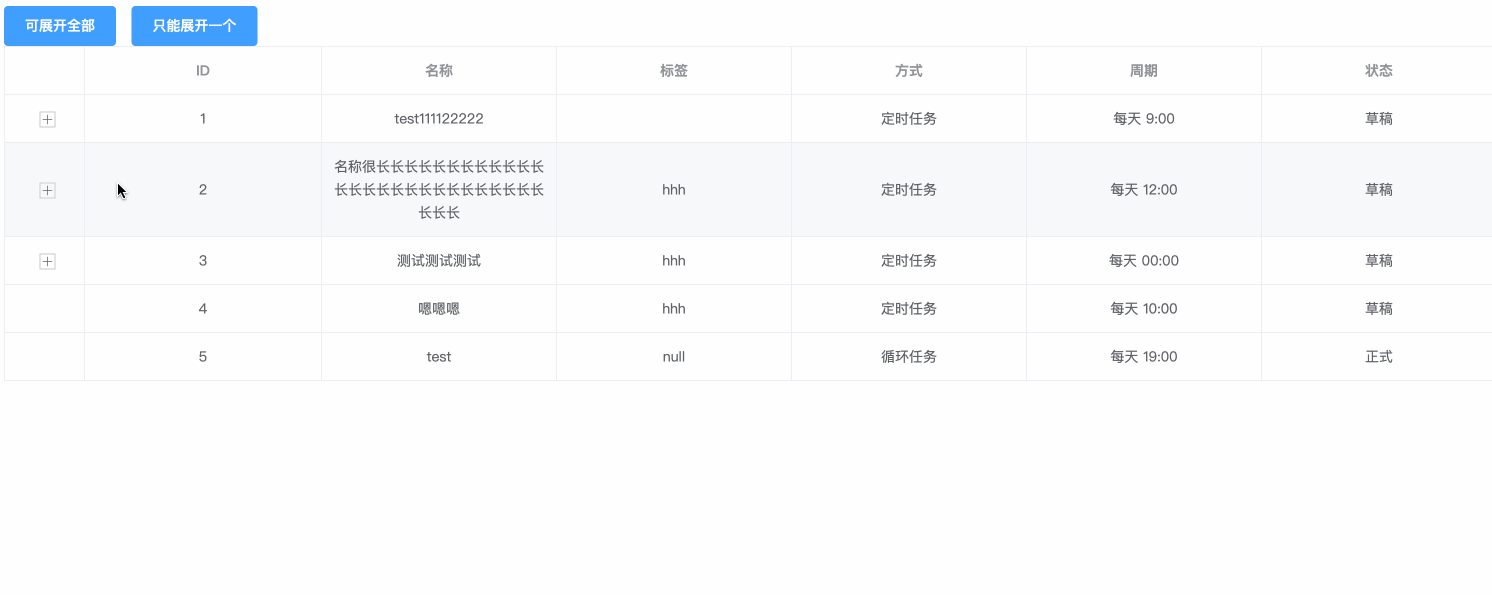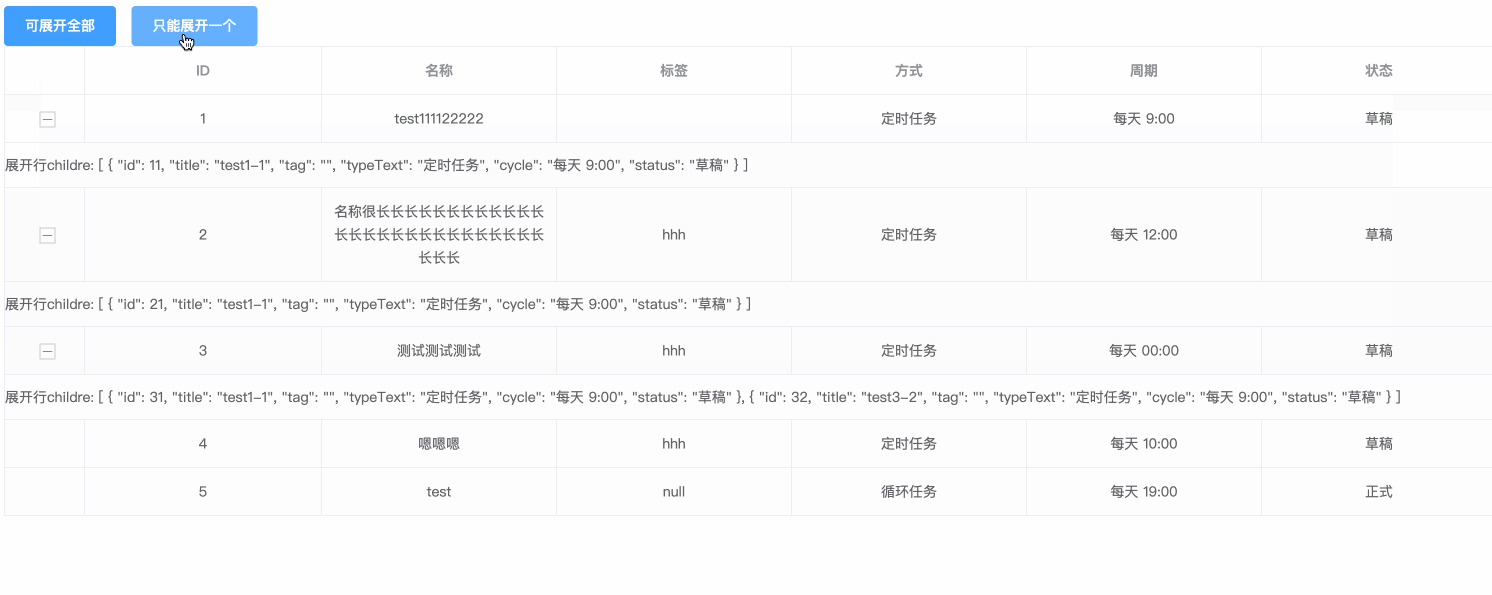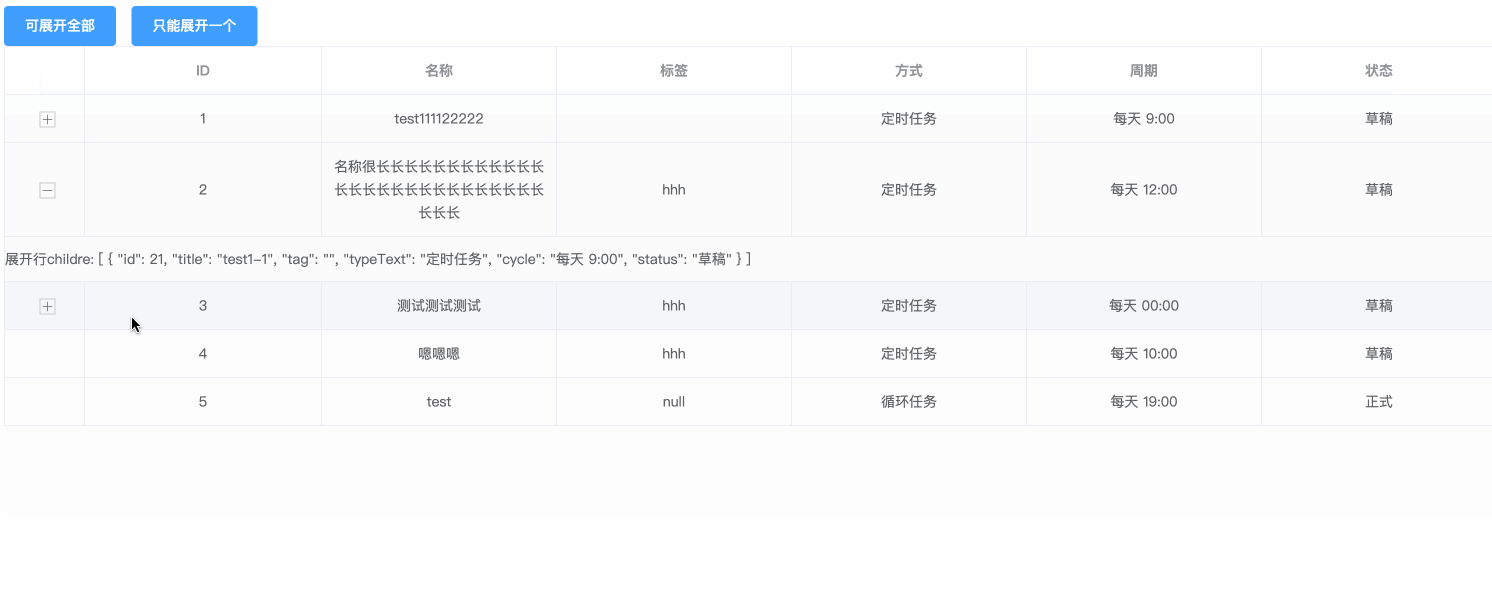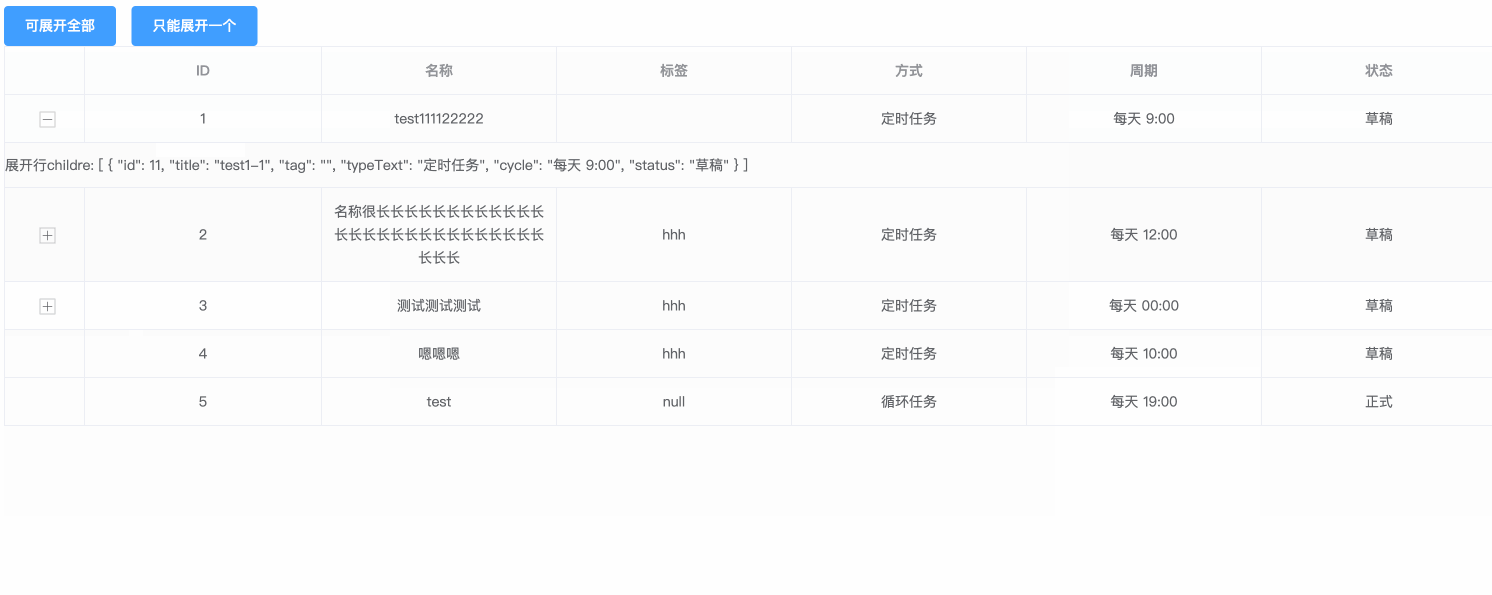
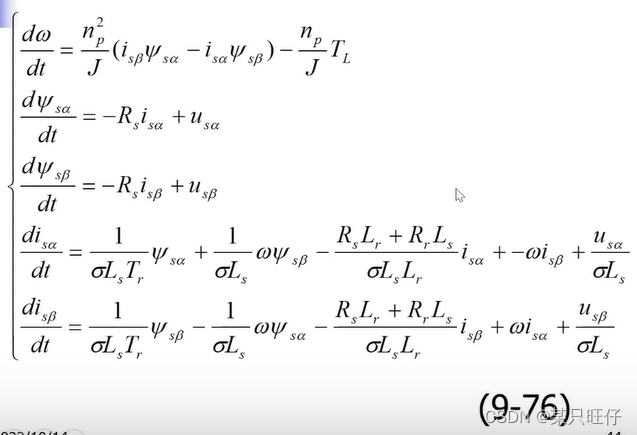目录
1、异步发电机在两相静止坐标系下的数学模型
(1)磁链方程:
(2)电压方程
(3)转矩方程
(4)异步电动机在两相静止坐标系( )上的数学模型
2、异步发电机在两相旋转坐标系下的数学模型
(1)磁链方程:
(2)电压方程:
(3)转矩方程:
3、异步发电机在两相坐标系上的状态方程
a、状态方程
(1)dq坐标系中的状态方程
(2)阿尔法,β坐标系中的状态方程
b、状态方程
(1)dq坐标系中的状态方程
(2)阿尔法,β坐标系中的状态方程
接上文:三相异步电动机的数学模型-CSDN博客
1、异步发电机在两相静止坐标系下的数学模型
- 定子坐标系变换:
坐标系——>
坐标系 利用三相两相变换
将定子ABC三相静止坐标系变换为
两相静止坐标系当中
- 转子坐标系变换:
坐标系——>
坐标系——>
坐标系 利用三相两相变换
将转子ABC三相旋转坐标系变换为
两相旋转坐标系,此时该坐标系以角速度
旋转,为了能够将定子和转子变换到同一个坐标系,因此要将
坐标系进行两相静止到两相旋转的逆变换
。

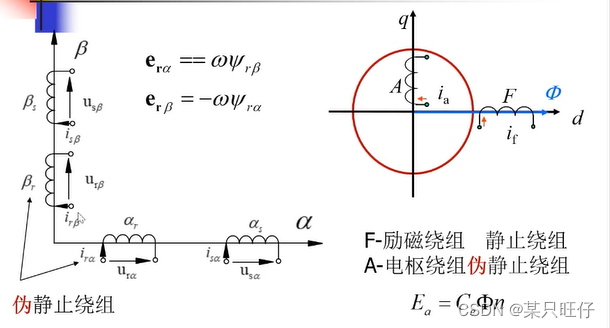
异步电动机转换到两相静止坐标系的物理模型(右上角为磁链方程)
每个磁链方程计算时,都包括自身电感的自感,以及与其坐标系重叠后另一方的互感,自身为定子,那另一方就为转子,自身为转子,另一方就为定子。
(1)磁链方程:


两相静止坐标系的优点:
比较三相异步电动机的aβ坐标系磁链方程式(9-44)和ABC坐标系磁链方程式 ,可以看出,采用坐标变换简化数学模型时,通过3/2变换将互差.120°的三相绕组等效成正交的两相绕组,互感磁链只在同轴绕组间存在,从而消除了三相绕组之间的耦合关系,6X 6的电感矩阵简化成4X4电感矩阵。3/2 变换减少了状态变量的维数,同时矩阵中的0增多,简化了定子和转子的自感矩阵。
(原因: 互感系数为一个线圈中由于另一个线圈中单位电流变化而引起的磁通量的变化.平面线圈在轴线方向上磁场近似是沿着轴线方向的,如果将另一个线圈沿其轴线方向放置,也就是垂直放置,这时第一个线圈在第二个线圈上产生的磁通量为0;当第一个线圈中的电流变化时,第二个线圈的磁通量始终为0,因而互感系数为0。因此当两轴垂直时,位于两轴上的电感之间不发生互感)
原本的6X 6的电感矩阵:

变化后的4X4电感矩阵:

(2)电压方程

其中为切割电动势

将(9-45)的向量表达形式为:

(3)转矩方程
定子电流和转子电流相互作用后产生的转矩。
因此将转矩方程式中的三相电流变换到两相静止坐标系上,得到 坐标系中的转矩方程

(4)异步电动机在两相静止坐标系( 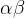 )上的数学模型
)上的数学模型
式(9-44)(关于的方程式),(9-45)(关于
的方程式),(9-47)(关于
定转子电流相互作用的方程式)和运动方程式,构成了
坐标系中的异步电动机动态数学模型,又称为Kron的异步电动机方程式或双轴原型电动机基本方程式。

在坐标系中数学模型是三相数学模型经过3/2变换和旋转变换后得到的,旋转变换改变了定、转子绕组之间的耦合关系,将相对运动的定、转子绕组用相对静止的等效绕组来代替,从而消 除了定、转子绕组间夹角对磁链和转矩的影响。
旋转变换的优点在于将非线性变参数的磁链方程转化为线性定常的方程,但却加剧了电压方程中的非线性耦合程度。用变换后坐标模型进行分析和设计要简单得多,但系统非线性、强耦合的性质并未改变。
2、异步发电机在两相旋转坐标系下的数学模型
两相坐标系可以是静止的,也可以是旋转的。如果按照某--特定速度进行旋转,则可以达到解耦的作用,使异步电动机可以按照直流电动机那样进行控制。按照同步转速进行旋转变换的情况,即同步旋转坐标系上异步电动机的数学模型。
在两相同步旋转坐标系(以下称为dq 坐标系)中的模型,其旋转速度等于定子频率的同步角转
速,即dq坐标系相对定子的旋转角转速为
。
由于dq坐标系和电动机中旋转磁场的旋转速度是相同的,当ABC坐标系中的电压和电流是在
电源频率下的正弦函数时,变换到dq坐标系中的电压和电流是直流。
通过Park 变换可以将三相模型变换成dq 模型。此处略去推导过程,直接给出变换后的方程。转子的角速度为,dq 轴相对转子的角转速
即转差。

异步电动机在两相同步旋转坐标系的物理模型
(1)磁链方程:

(2)电压方程:

(3)转矩方程:

式(9-48),(9-49),(9-51)和运动方程式构成了异步电动机在两相同步旋转坐标系的数学模型。
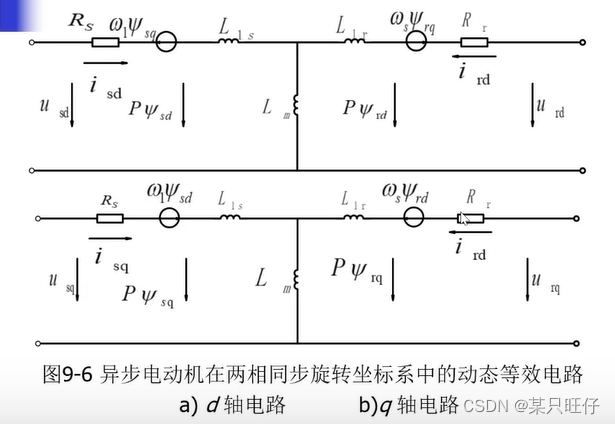
将式(9-49)的dq 坐标系中的电压方程绘成动态等效电路,如图9-6所示。图9-6a是d轴电路,图9-6b是q轴电路,它们之间靠4个旋转电动势互相耦合。图9-6中所有表示电压或电动势的箭头都是按电压降方向画的。
3、异步发电机在两相坐标系上的状态方程
以上用矩阵方程的形式,给出了异步电动机在两相坐标系上的数学模型。在某些情况下,状态方程形式的数学模型使用起来会更加方便。为此,下面介绍异步电动机在两相坐标系上的状态方程。
由式(9-45)和(9-49)可知,异步电动机在两相坐标系上的电压方程是四阶的,再加上一一阶的运动方程,其状态方程应该是五阶的,需要选取五个状态变量。而可选的变量共有九个,即转速、定子电流
、转子电流
、,定子磁链
以及转子磁链
。
转速作为输出变量必须选取,定子电流可以直接检测,应当选为状态变量,而转子电流是不可测的不宜用作状态变量。考虑到磁链对电动机运行的重要性,可以在定子磁链和转子磁链中任选一组。
- (1) 采用转速
、定子电流
、转子磁链
构成的状态方程,称为
状态方程,矢量控制方法就选用这组状态方程。
- (2)采用转速
、定子电流
、定子磁链
构成的状态方程,称为
状态方程,直接转矩控制方法就选用这组状态方程。
a、 状态方程
状态方程
(1)dq坐标系中的状态方程
选取状态变量
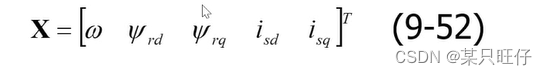
输入变量

输出变量
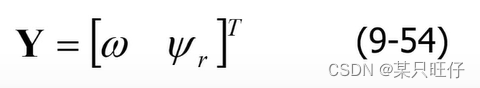
dq坐标系中的磁链方式如式(9-48),表达如下:

将式(9-49)电压方程改写成
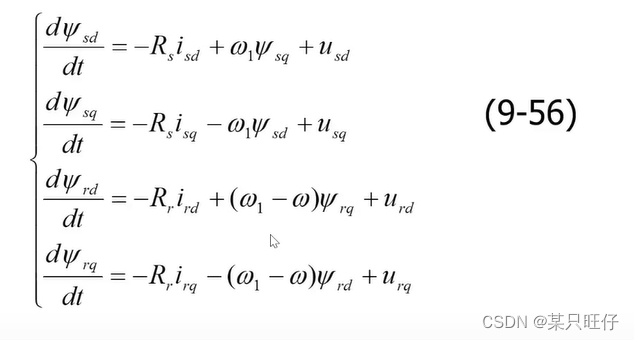
考虑到笼型转子内部是短路的,则,则电压方程可写成

由式(9-55)中第三、四两式可解出

代入转矩方程式(9-51),得
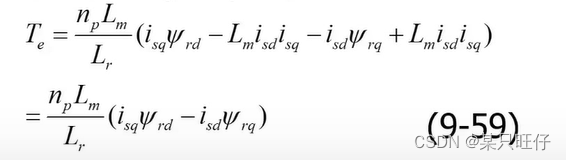
将(9-58)代入式(9-55)的前两行,


将式(9-58)和式(9-60)代入微分方程式(9-57),消去,再将转矩方程(9-51)代入运动方程式,经整理后即得状态方程。
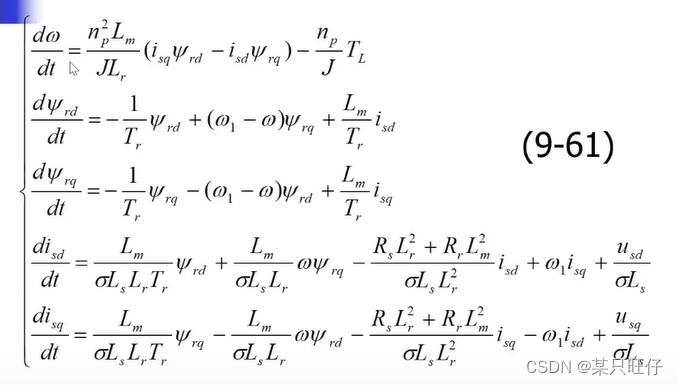

(2)阿尔法,β坐标系中的状态方程
若令,dq 坐标系蜕化成
坐标系,可得
坐标系中的状态方程


b、 状态方程
状态方程
(1)dq坐标系中的状态方程



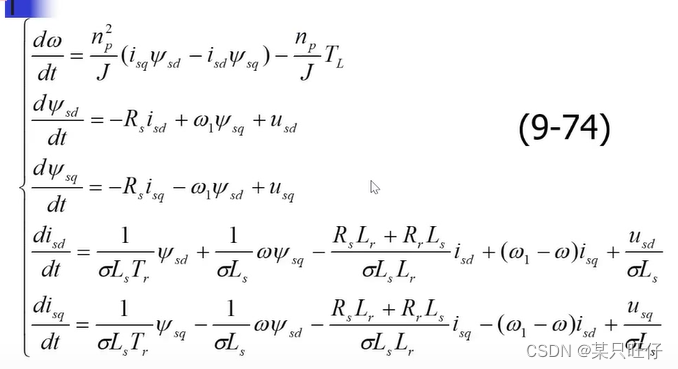

(2)阿尔法,β坐标系中的状态方程
同样,若令,可得
坐标系中的状态方程。