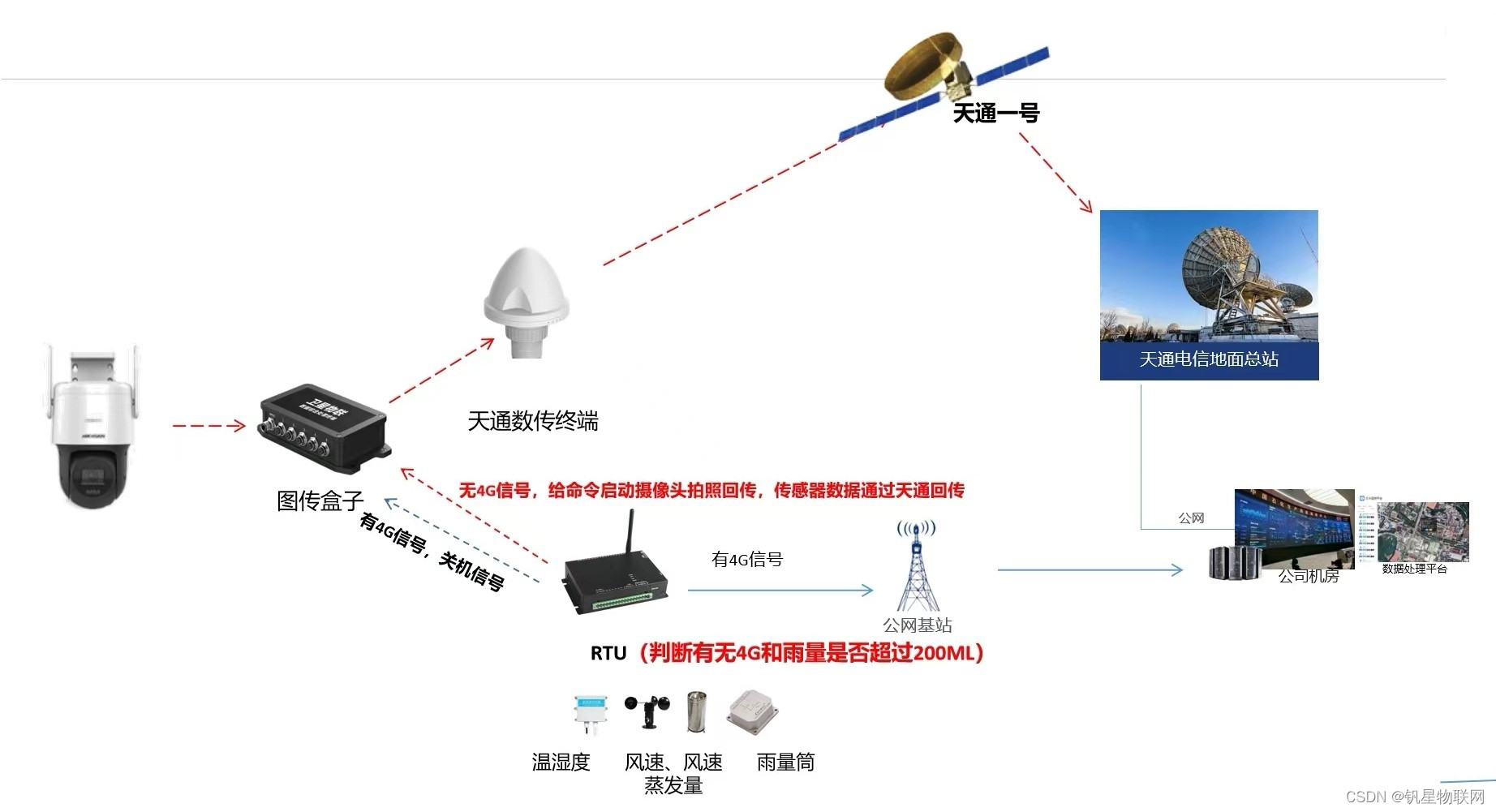
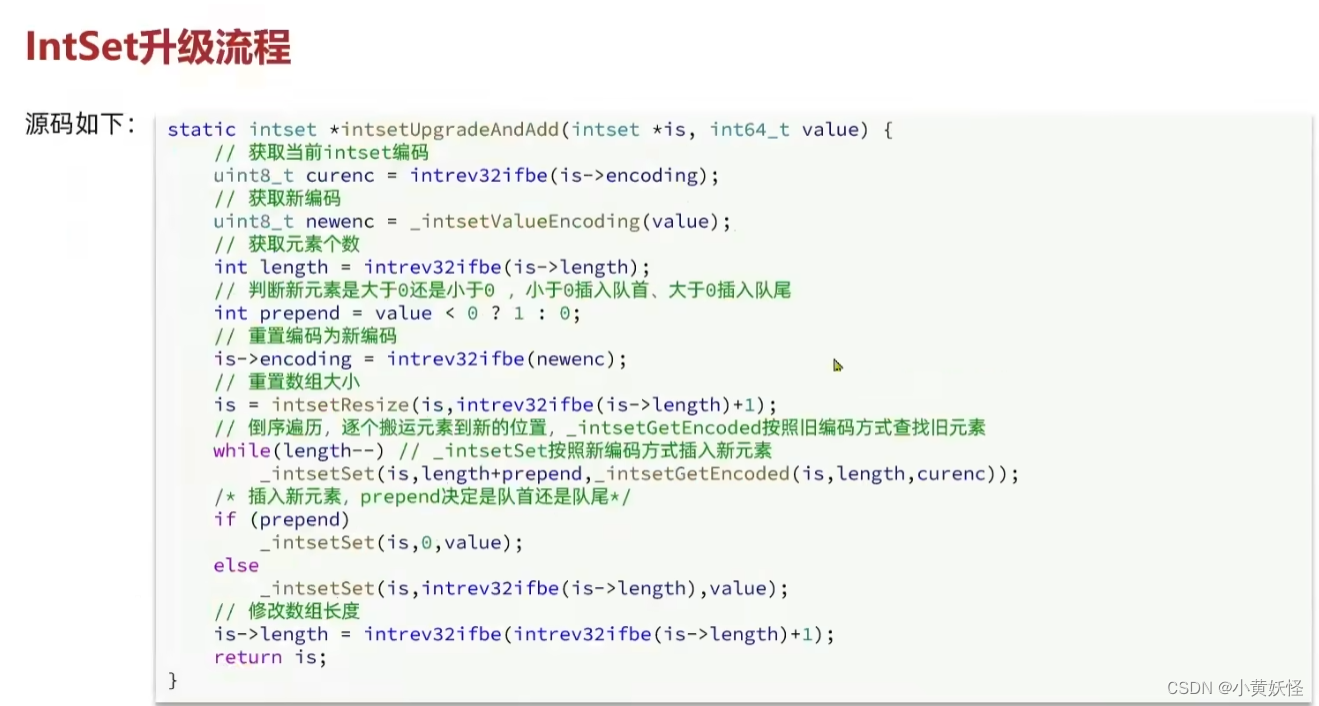
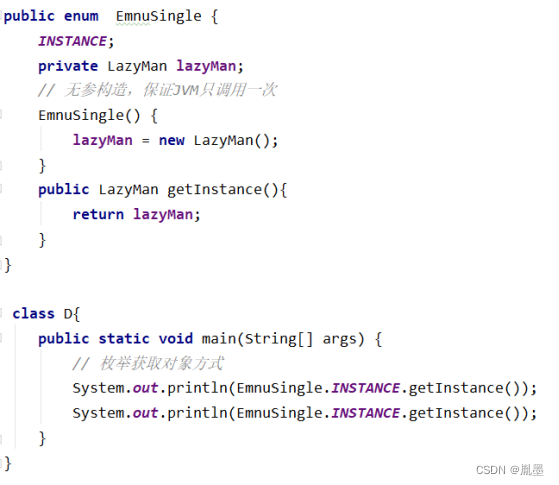
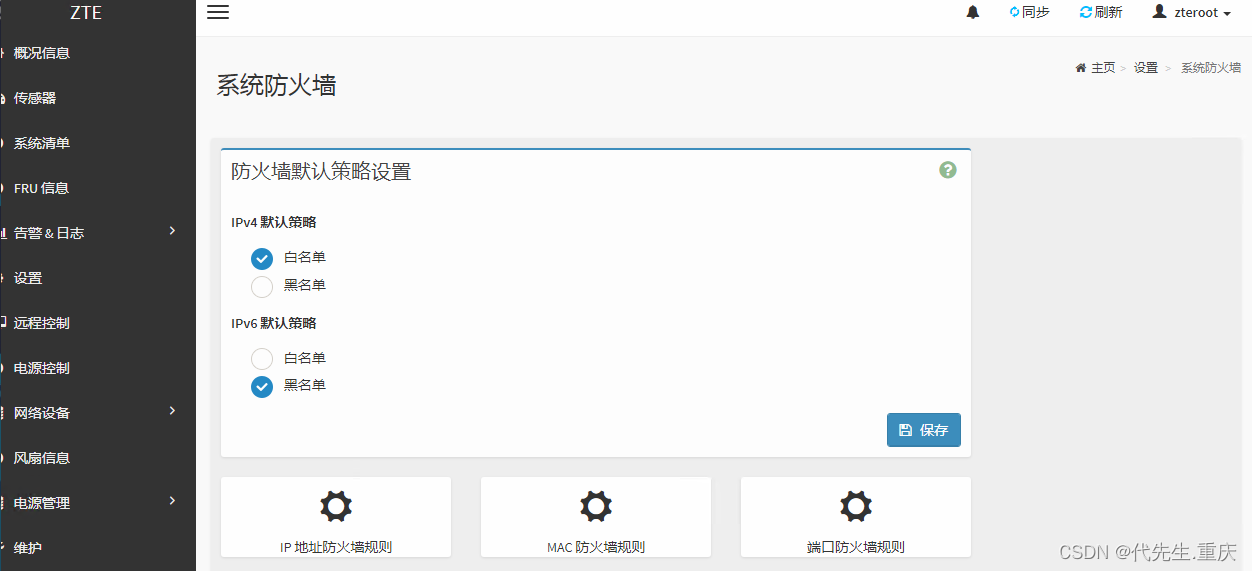
算法概述

高斯消元法是一个用来求解线性方程组的算法

那么什么是线性方程组呢?

线性:每个未知数次数都为1次方程组:多个方程，多个未知数。

（a1x1+a2x2+..+anxn=bn）x为一次的

当x是平方的时候就不是线性

简而言之就是有多个未知数，并且每个未知数的次数均为一次，这样多个未知数组成的方程组为一

性方程组。或者我们也可以说是多元一次方程组

问题引入

给定一个线性方程组，对其求解

2x+y-z=8

-3x-y+2z=11

-2x+y+2z=-1

加减消元法和代入消元法

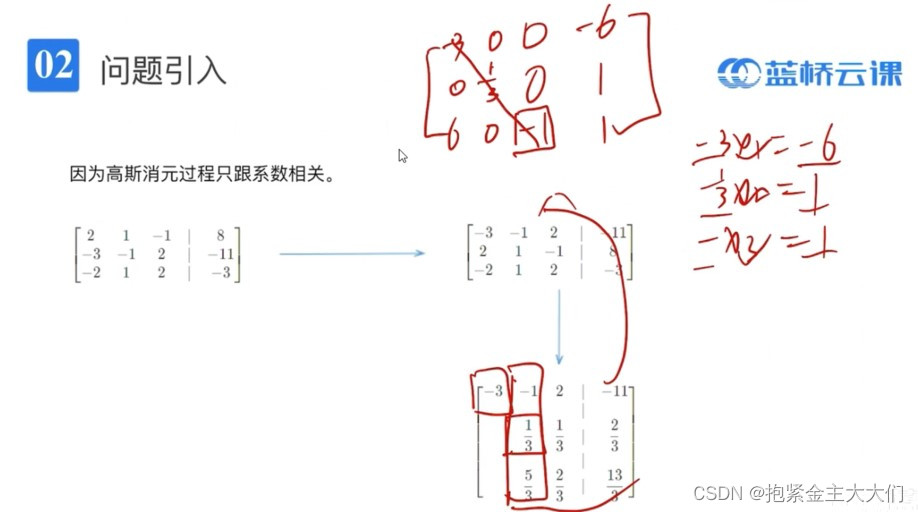
 高斯消元的目的是，先进行加减消元，然后我们可以先求得一个未知数的值，然后可以逐层往回代，也就是代入消元法，依次可以得到定第2个、第3个未知数的值，以至第n个未知数。最终解出方程组中各个未知数。

加减消元

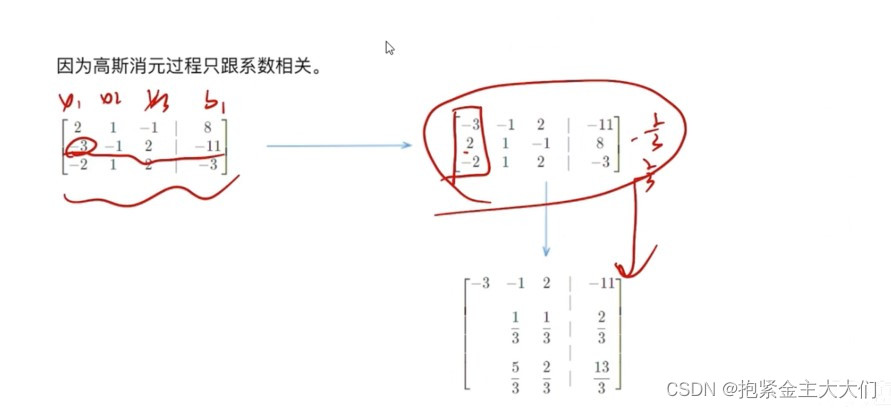
对第一列进行操作（绝对值最大的一行，交换到第一行）

寻找最大值的原因是因为观察是否已经全是0了。

第二行减去若干倍的第一行，用第三行减去若干倍的第一行

高斯消元的代码详解

package gaosixiaoyuan;

import java.util.*;
import java.util.BitSet;

public class chapter1 {
	static final int N = 2800;
    static BitSet[] a = new BitSet[N];
    static int n, m, x, ans;
	public static void main(String[] args) {
		// TODO Auto-generated method stub
		Scanner scanner = new Scanner(System.in);
        n = scanner.nextInt();
        for (int i = 1; i <= n; i++) {
            a[i] = new BitSet(n + 1);
            m = scanner.nextInt();
            if (m % 2 != 0) {
                a[i].set(n + 1);
                a[i].set(i);
            }
            while (m-- > 0) {
                x = scanner.nextInt();
                a[i].set(x);
            }
        }
        gauss();
	}
	public static void gauss() {
		        int cnt = 0;
		        for (int i = 1; i <= n; i++) {
		            int maxx = cnt + 1;
		            for (int j = i + 1; j <= n; j++) {
		                if (a[j].get(i) && !a[maxx].get(i)) maxx = j;
		            }
		            BitSet temp = a[cnt + 1];
		            a[cnt + 1] = a[maxx];
		            a[maxx] = temp;
		            if (!a[i].get(i)) continue;
		            cnt++;
		            for (int j = 1; j <= n; j++) {
		                if (a[j].get(i) && i != j) a[j].xor(a[i]);
		            }
		        }
		        if (cnt < n) {
		            for (int i = 1; i <= n; i++) {
		                if (!a[i].get(i) && a[i].get(n + 1)) 
		                	System.out.println("no solution");
		            }
		        }
		    }
}

 综上所述，可以大致分为三种情况：

1.高斯消元完成后，若存在系数全为0、常数不为0的行，则方程组无解。

2.若系数不全为0的行恰好有n个，则主元有n个，方程组有唯一解。

3.系数不为0的行<n个，则有无数个解。