2012年认证杯SPSSPRO杯数学建模A题(第一阶段)蜘蛛网全过程文档及程序

news2024/10/6 22:21:13

2012年认证杯SPSSPRO杯数学建模

A题 蜘蛛网

原题再现：

  第一阶段问题
  世界上生存着许多种类的蜘蛛，而其中的大部分种类都会通过结网来进行捕食。请你建立合理的数学模型，说明蜘蛛网织成怎样的结构才是最合适的。

整体求解过程概述(摘要)

  众所周知，蜘蛛是一个比较庞大的物种，而蜘蛛网也在世界各地都存在着。通过人们长时间来的观察与研究，渐渐发现了蜘蛛网其结构内部的本质。作为一个长时间来捕捉猎物的利器，无论从材料的柔韧性，阻尼运动对蛛网强度的保护性，还是对紫外线光的反射性，都从各个方面反映出了蜘蛛网对于蜘蛛捕食关键性的作用。那么，面对蜘蛛网诸多性质，我们从另一方面，即蜘蛛网的结构密集度计算、建模并优化来分析蜘蛛网在捕食方面的另一重要作用。
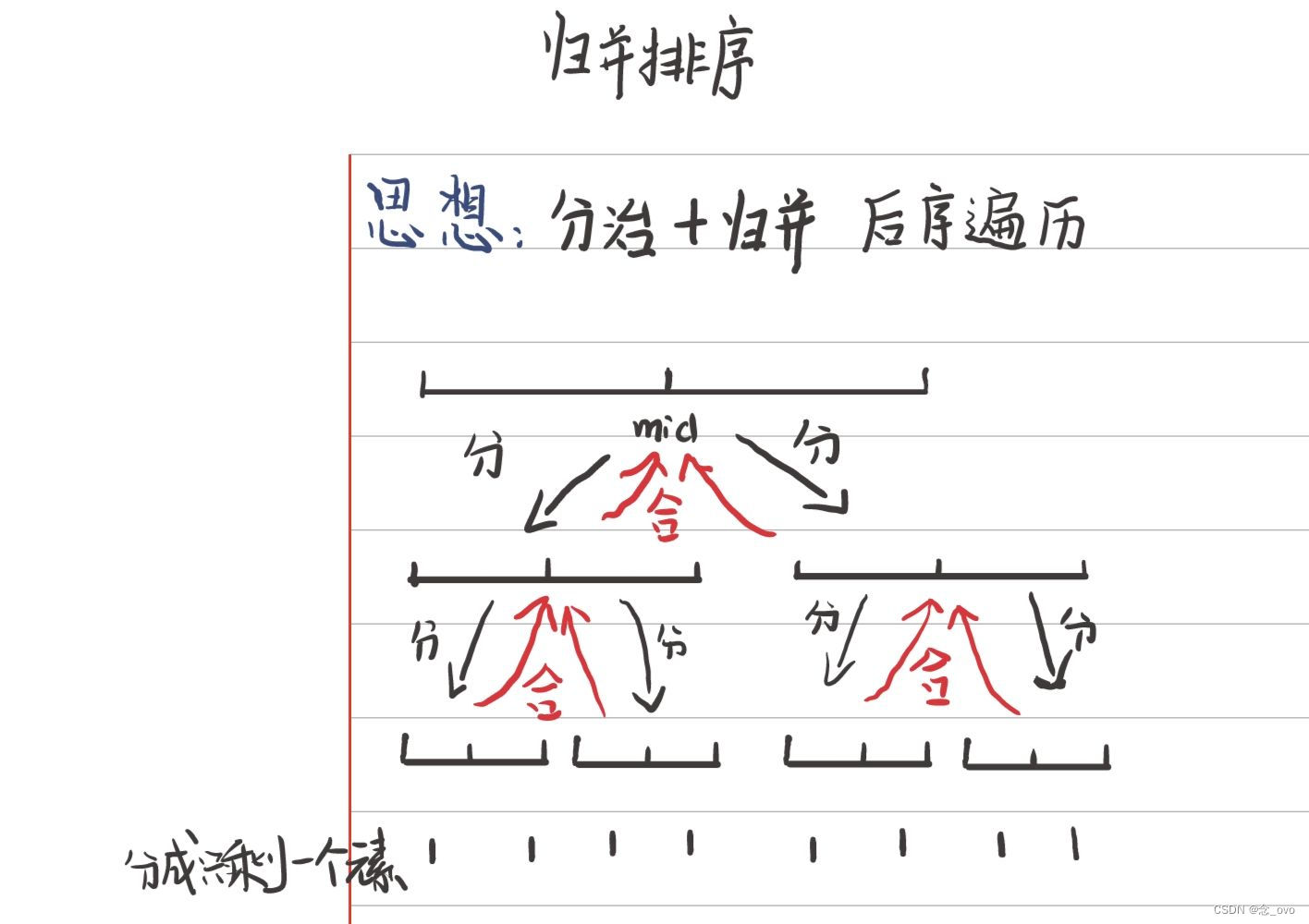
  在建模过程中，我们总体上通过构造蛛网模型模拟蛛网捕虫的过程，并通过计算捕虫随机过程的概率来优化蛛网模型。首先对于蛛网的建立，我们通过模拟蛛网的构架，即确定初始半径的大小和方向来确定蛛网以后的螺旋编织的方向和大小。其次，再在已有的蛛网架构基础上进行螺旋形展开，通过对蛛网网格的密集度限制条件对其展开进行限制，从而获得初步蛛网模型。在完成了初步的蛛网模型后，我们将把蛛网模型应用到一个空间的捕虫模拟中，在该模拟过程中，通过计算该蛛网捕虫成功的概率来验证所建蛛网的合理性。如不满足优化因子，我们将通过改变蛛网架构的初值来优化蛛网的结构。
  最后，我们将综合蛛网所受张力以及在捕虫过程中的阻尼运动等物理问题，将所建立的蛛网模型应用到实际问题中，并进一步通过 GA 算法对其进行进一步优化，更加仿真地模拟蛛网的构造，方便以后的研究。

问题分析：

  我们知道，在生物界的成长与优胜劣汰中，蜘蛛以其强大的生命力和竞争能力在生物界顽强生长了一亿多年，不论周遭环境如何，都可以顽强的生存下来，由此可知，蜘蛛网对于蜘蛛得以在生物界顺利存活如此之长的时间起到了至关重要的作用。自然而然的，对于至关重要的蛛网的结构、物理特性等方面的研究也就吸引了很多眼球。
  第一，在结构方面，蛛网的特性之所以可以捕捉到许多昆虫，并且可以长时间编织在角落里，是与蛛网的结构密集性与稳定性是不可分割的。首先，对于蛛网密集性的分析，我们可以发现，如果不是蛛网密集度性能好，昆虫是无法大概率的被捕捉的。所以我们从蛛网的密集度着手，首先根据蛛网的密集性对蛛网的初始值进行编译，通过对许多外界因素的参考与分析进行初步参数设定，同时对建立好的初步模型螺旋展开，同时并运用 GA 算法（遗传算法）对展开后的螺旋性图进行优化处理，并得出最终密集度相对较好的蛛网。其次，通过分析蛛网的稳定性，我们再对建立出的蛛网设立密集系数，对建立出的蛛网每个模块的面积及其相互之间的受力关系进行稳定测定，如果不满足我们设定的密集系数范围，则通过改变相应的初始参数来尽量满足最终的蛛网稳定性。
  第二，在物理方面，蛛网无论在力学方面还是在光学方面都有着奇特的性质。所以，我们首先将分析蛛网间的受力以及蛛网总体的重力影响来研究蛛网之所以稳定不易掉落损坏的愿意。其次，通过分析动物在撞击蛛网后，蛛网之所以可以承受住动物巨大的冲击，是与其特别的阻尼运动分不开的，所以，在力学方面，蛛网有着其特殊的性质，所以，根据这些特点，我们可以针对蛛网的结构展开进行讨论与研究。另外，正是由于光反射的原因，蛛网才得以顺利的诱惑昆虫撞向蛛网，所以，我们还可综合斜率或角度原因来对蛛网的展开角度进行构造。
  同时，在建立好的模型的基础上，我们可以根据已有的 GA 算法（遗传算法）对已有模型进行进一步分析和优化，并通过进一步的严谨将蛛网模型应用至更多的蜘蛛类别中，从而达到真正仿真实验的目的。

论文缩略图：

在这里插入图片描述
在这里插入图片描述

全部论文请见下方“ 只会建模 QQ名片” 点击QQ名片即可

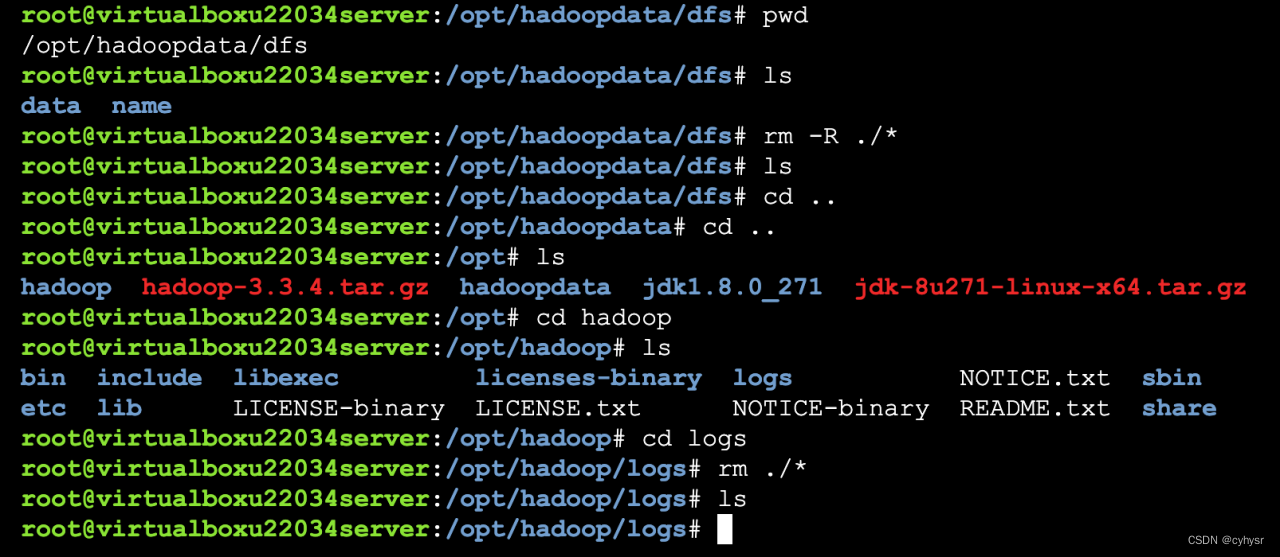
部分程序代码：(代码和文档not free)

clear;
clc;
hold on;
global sumlen;
sumlen=0;
nl=0;
plot([0,0],[-20,20],'--k');
plot([-20,20],[0,0],'--k');
%% init
infil=fopen('mat.in','r');
[n,num]=fscanf(infil,'%d',1);
[nesw,num]=fscanf(infil,'%f',4);
[abell,num]=fscanf(infil,'%f',8);
[tau,num]=fscanf(infil,'%f',1);
[rho,num]=fscanf(infil,'%f',n-1);
rho(n)=0;
[r0,num]=fscanf(infil,'%f',1);
[d,num]=fscanf(infil,'%f',1);
[k,num]=fscanf(infil,'%f',1);
[es,num]=fscanf(infil,'%f',1);
[id,num]=fscanf(infil,'%f',1);
alpha=2*pi/n;
%% ellipse
syms x y;
z=[((x-nesw(2))/abell(1))^2+(y/abell(2))^2-1+x;((y-nesw(1))/abell(2))^2+(x/
abell(1))^2-1+y];
[xy01,num]=mulStablePoint(z,[1;1]);
z=[((x-nesw(3))/abell(3))^2+(y/abell(4))^2-1+x;((y-nesw(2))/abell(4))^2+(x/
abell(3))^2-1+y];
[xy02,num]=mulStablePoint(z,[1;1]);
z=[((x-nesw(4))/abell(5))^2+(y/abell(6))^2-1+x;((y-nesw(3))/abell(6))^2+(x/
abell(5))^2-1+y];
[xy03,num]=mulStablePoint(z,[1;1]);
z=[((x-nesw(1))/abell(7))^2+(y/abell(8))^2-1+x;((y-nesw(4))/abell(8))^2+(x/
abell(7))^2-1+y];
[xy04,num]=mulStablePoint(z,[1;1]);
xxl=abell(1)*cos(0)+xy01(1);
yyl=abell(2)*sin(0)+xy01(2);
for beta=0.001:0.001:2*pi;
 xxn=abell(1)*cos(beta)+xy01(1);
 yyn=abell(2)*sin(beta)+xy01(2);
 if xxl>0 & xxn>0 & yyl>0 & yyn>0
 plot([xxl,xxn],[yyl,yyn],'w');
 end
 xxl=xxn;
 yyl=yyn;
end
xxl=abell(3)*cos(0)+xy02(1);
yyl=abell(4)*sin(0)+xy02(2);
for beta=0.001:0.001:2*pi;
 xxn=abell(3)*cos(beta)+xy02(1);
 yyn=abell(4)*sin(beta)+xy02(2);
 if xxl>0 & xxn>0 & yyl>0 & yyn>0
 plot([yyl,yyn],[-xxl,-xxn],'w');
 end
 xxl=xxn;
 yyl=yyn;
end
xxl=abell(5)*cos(0)+xy03(1);
yyl=abell(6)*sin(0)+xy03(2);
for beta=0.001:0.001:2*pi;
 xxn=abell(5)*cos(beta)+xy03(1);
 yyn=abell(6)*sin(beta)+xy03(2);
 if xxl>0 & xxn>0 & yyl>0 & yyn>0
 plot([-xxl,-xxn],[-yyl,-yyn],'w');
 end
 xxl=xxn;
yyl=yyn;
end
xxl=abell(7)*cos(0)+xy04(1);
yyl=abell(8)*sin(0)+xy04(2);
for beta=0.001:0.001:2*pi;
 xxn=abell(7)*cos(beta)+xy04(1);
 yyn=abell(8)*sin(beta)+xy04(2);
 if xxl>0 & xxn>0 & yyl>0 & yyn>0
 plot([-yyl,-yyn],[xxl,xxn],'w');
 end
 xxl=xxn;
 yyl=yyn;
end
%% main line
theta=pi/2-tau*2*pi/360;
for i=1:1:n
 if theta>0
 
[p(i,1),p(i,2)]=drawmainline(tan(theta),abell(1),abell(2),xy01(1),xy01(2),1
);
 else
 if theta>-pi/2
 
[p(i,1),p(i,2)]=drawmainline(tan(theta+pi/2),abell(3),abell(4),xy02(1),xy02
(2),2);
 else
 if theta>-pi
 
[p(i,1),p(i,2)]=drawmainline(tan(theta+pi),abell(5),abell(6),xy03(1),xy03(2
),3); 
 else if theta>-3/2*pi 
 
[p(i,1),p(i,2)]=drawmainline(tan(theta+pi*3/2),abell(7),abell(8),xy04(1),xy
04(2),4);
 else
 
[p(i,1),p(i,2)]=drawmainline(tan(theta+2*pi),abell(1),abell(2),xy01(1),xy01
(2),1);
 end
 end
 end
 end
 theta=theta-alpha-rho(i)*2*pi/360;
end
for i=1:1:n-1
 plot([p(i,1),p(i+1,1)],[p(i,2),p(i+1,2)],'--k');
end
plot([p(n,1),p(1,1)],[p(n,2),p(1,2)],'--k');
%% line
l=len(p(1,1),p(1,2));
lastx=r0*p(1,1)/l;
lasty=r0*p(1,2)/l;
r=r0;
rr(1)=r0;
for i=1:1:n-1
r=r+d;
 rr(i+1)=r;
 l=len(p(i+1,1),p(i+1,2));
 nowx=r*p(i+1,1)/l;
 nowy=r*p(i+1,2)/l;
 plot([lastx,nowx],[lasty,nowy]);
 nl=nl+1;
 line(nl,1)=(lasty-nowy)/(lastx-nowx);
 line(nl,2)=lasty-line(nl,1)*lastx;
 line(nl,3)=lastx;
 line(nl,4)=nowx;
 lastx=nowx;
 lasty=nowy;
end
r=r+d;
rr(1)=r;
l=len(p(1,1),p(1,2));
nowx=r*p(1,1)/l;
nowy=r*p(1,2)/l;
plot([lastx,nowx],[lasty,nowy]);
nl=nl+1;
line(nl,1)=(lasty-nowy)/(lastx-nowx);
line(nl,2)=lasty-line(nl,1)*lastx;
line(nl,3)=lastx;
line(nl,4)=nowx;
lastx=nowx;
lasty=nowy;
flag=0;
i=2;
ii=1;
d=d*(n-1)*k;
while 1
 if i>n
 i=i-n;
 end
 if i<1
 i=i+n;
 end
 r=rr(i)+d;
 l=len(p(i,1),p(i,2));
 if l<r
 if flag==1
 break;
 end
 ii=-ii;
 i=i+2*ii;
 flag=1;
 continue;
 end
 nowx=r*p(i,1)/l;
 nowy=r*p(i,2)/l;
 plot([lastx,nowx],[lasty,nowy]);
 rr(i)=r;
 sumlen=sumlen+len(lastx-nowx,lasty-nowy);
 nl=nl+1;
 line(nl,1)=(lasty-nowy)/(lastx-nowx);
 line(nl,2)=lasty-line(nl,1)*lastx;
line(nl,3)=lastx;
 line(nl,4)=nowx;
 lastx=nowx;
 lasty=nowy;
 i=i+ii;
 flag=0;
 d=d*k;
end
%% simulation
sumv=0;
v=0;
for i=1:1:10000
 ix=25*rand(1,1);
 iy=25*rand(1,1);
 is=normrnd(es,id);
 while is<0
 is=normrnd(es,id);
 end
 v=v+is^3;
 for j=1:1:nl
 dis=abs(line(j,1)*ix+line(j,2)-iy)/sqrt(line(j,1)^2+1);
 if dis>is
 continue;
 end
 
tdeta=sqrt(-2*ix*(line(j,2)-iy)+is*is*(1+line(j,1)^2)-line(j,1)^2*(ix*ix+(l
ine(j,2)-iy)^2));
 tx=(ix-(line(j,2)-iy)-tdeta)/(1+line(j,1)^2);
 if (line(j,3)-tx)*(line(j,4)-tx)<0
 sumv=sumv+is^3;
 break;
 end
 tx=(ix-(line(j,2)-iy)+tdeta)/(1+line(j,1)^2);
 tx=(ix-(line(j,2)-iy)-tdeta)/(1+line(j,1)^2);
 if (line(j,3)-tx)*(line(j,4)-tx)<0
 sumv=sumv+is^3;
 break;
 end 
 end
end
%% outit
sumlen
sumv
rate=sumv/v
%% program end
axis('equal');
fclose(infil);
hold off;
全部论文及程序请见下方“ 只会建模 QQ名片” 点击QQ名片即可

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1564631.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

ubuntu-server部署hive-part2-安装hadoop

ubuntu-server部署hive-part2-安装hadoop

参照 https://blog.csdn.net/qq_41946216/article/details/134345137 操作系统版本&#xff1a;ubuntu-server-22.04.3 虚拟机&#xff1a;virtualbox7.0 安装hadoop ​​​​​​下载上传 下载地址 https://archive.apache.org/dist/hadoop/common/hadoop-3.3.4/ 以root用…
阅读更多...
Ps：HDR 色调

Ps：HDR 色调

HDR 技术旨在通过合并不同曝光度的图像来扩展照片的光照细节范围&#xff0c;使得最终图像能够同时展示最亮和最暗区域的细节。 HDR 色调 HDR Toning命令能够在单张图像上重现类似的效果&#xff0c;无需多张不同曝光的照片。 Ps菜单&#xff1a;图像/调整/HDR 色调 Adjustment…
阅读更多...
【EasyExcel】—— 实现excel动态表头设置、多个sheet

【EasyExcel】—— 实现excel动态表头设置、多个sheet

引入jar <dependency><groupId>com.alibaba</groupId><artifactId>easyexcel</artifactId><version>3.1.0</version></dependency>代码 public static void main(String[] args) {//选择存储地址String fileName "/User…
阅读更多...
【25考研】：四川大学计算机学院24届874考研考情分析

【25考研】：四川大学计算机学院24届874考研考情分析

去年的考情分析也是我做的&#xff0c; 今年就在去年的基础上做了。保持形式不变&#xff0c;更改数据。 21考情&#xff1a; 万载月寒肠断客&#xff1a;四川大学计算机学院21届CS考研考情分析 22考情&#xff1a; 懒羊羊&#xff1a;四川大学计算机学院2022考研考情分析 2…
阅读更多...
Taro + vue3 小程序封装标题组件

Taro + vue3 小程序封装标题组件

分为没有跳转页面的title组件和 有跳转页面的title组件 我们可以把这个封装成一个组件 直接上代码 <template><div class"fixed-title-container"><div class"box"><div class"icon" v-if"isShow" click"…
阅读更多...
Android的图片加载框架

Android的图片加载框架

Android的图片加载框架 为什么要使用图片加载框架&#xff1f;图片加载框架1. Universal Image Loader [https://github.com/nostra13/Android-Universal-Image-Loader](https://github.com/nostra13/Android-Universal-Image-Loader)2. Glide [https://muyangmin.github.io/gl…
阅读更多...
【C++】排序算法 --快速排序与归并排序

【C++】排序算法 --快速排序与归并排序

目录 颜色分类&#xff08;数组分三块思想&#xff09;快速排序归并排序 颜色分类&#xff08;数组分三块思想&#xff09; 给定⼀个包含红⾊、⽩⾊和蓝⾊、共 n 个元素的数组 nums &#xff0c;原地对它们进⾏排序&#xff0c;使得相同颜⾊ 的元素相邻&#xff0c;并按照红⾊、…
阅读更多...
文本自动粘贴编辑器：支持自动粘贴并筛选手机号码，让信息处理更轻松

文本自动粘贴编辑器：支持自动粘贴并筛选手机号码，让信息处理更轻松

在信息时代的浪潮中&#xff0c;文本处理已成为我们日常工作与生活的重要组成部分。无论是商务沟通、社交互动还是个人事务处理&#xff0c;手机号码的筛选与粘贴都显得尤为关键。然而&#xff0c;传统的文本处理方式效率低下、易出错&#xff0c;已无法满足现代人的高效需求。…
阅读更多...
Linux基础篇：VMware centos7虚拟机网络配置——桥接模式

Linux基础篇：VMware centos7虚拟机网络配置——桥接模式

VMware centos7虚拟机网络配置——桥接模式 1 搞清楚什么是桥接模式 桥接模式允许虚拟机直接连接到物理网络&#xff0c;就像它是物理网络中的一个独立设备一样。在这种模式下&#xff0c;虚拟机将具有与宿主机相同网络中的其他设备相同的网络访问权限。虚拟机将获得一个独立…
阅读更多...
MySQL-linux安装-万能RPM法

MySQL-linux安装-万能RPM法

一、MySQL的Linux版安装 1、 CentOS7下检查MySQL依赖 1. 检查/tmp临时目录权限&#xff08;必不可少&#xff09; 由于mysql安装过程中&#xff0c;会通过mysql用户在/tmp目录下新建tmp_db文件&#xff0c;所以请给/tmp较大的权限。执行 &#xff1a; chmod -R 777 /tmp2. …
阅读更多...
FPGA常用IP核之FIFO学习

FPGA常用IP核之FIFO学习

IP核是FPGA芯片公司提供的逻辑功能块&#xff0c;在FPGA芯片中可以进行优化和预先配置&#xff0c;可以直接在用户设计的程序中使用&#xff0c;应用范围很广。在FPGA设计开发过程中使用IP核&#xff0c;可以大大的缩短开发周期&#xff0c;高度优化的IP核可以使FPG开发工程师专…
阅读更多...
某音乐平台歌曲信息逆向之参数寻找

某音乐平台歌曲信息逆向之参数寻找

如何逆向加密参数&#xff1a;某音乐平台歌曲信息逆向之webpack扣取-CSDN博客 参数构建 {"comm": {"cv": 4747474,"ct": 24,"format": "json","inCharset": "utf-8","outCharset": "ut…
阅读更多...
如何开发创建自己的npm包并成功发布、维护至npm官方网站

如何开发创建自己的npm包并成功发布、维护至npm官方网站

npm&#xff0c;全称为Node Package Manager&#xff0c;是专为JavaScript生态系统设计的软件包管理系统&#xff0c;尤其与Node.js平台紧密关联。作为Node.js的默认包管理工具&#xff0c;npm为开发者提供了便捷的方式来安装、共享、分发和管理代码模块。 npm作为JavaScript世…
阅读更多...
【Python面试题收录】Python的可变对象与不可变对象

【Python面试题收录】Python的可变对象与不可变对象

一、可变对象与不可变对象的定义 在Python中&#xff0c;对象的可变性是指对象的内部状态&#xff08;值&#xff09;是否允许在对象创建后发生改变。根据这一特性&#xff0c;Python的数据类型可以分为两大类&#xff1a;可变对象&#xff08;mutable objects&#xff09;和不…
阅读更多...
Nginx三大常用功能“反向代理，负载均衡，动静分离”

Nginx三大常用功能“反向代理，负载均衡，动静分离”

注意&#xff1a;以下案例在Windows系统计算机作为宿主机&#xff0c;Linux CentOS 作为虚拟机的环境中实现 一&#xff0c;Nginx配置实例-反向代理 1.反向代理 案例一 实现效果&#xff1a;使用nginx反向代理&#xff0c;访问 www.123.com 直接跳转到127.0.0.1:8080 准备工…
阅读更多...
大数据学习第十二天（hadoop概念）

大数据学习第十二天（hadoop概念）

1、服务器之间数据文件传递 1&#xff09;服务器之间传递数据&#xff0c;依赖ssh协议 2&#xff09;http协议是web网站之间的通讯协议&#xff0c;用户可已通过http网址访问到对应网站数据 3&#xff09;ssh协议是服务器之间&#xff0c;或windos和服务器之间传递的数据的协议…
阅读更多...
STM32-03基于HAL库（CubeMX+MDK+Proteus）输入检测案例（按键控制LED）

STM32-03基于HAL库（CubeMX+MDK+Proteus）输入检测案例（按键控制LED）

文章目录 一、功能需求分析二、Proteus绘制电路原理图三、STMCubeMX 配置引脚及模式&#xff0c;生成代码四、MDK打开生成项目&#xff0c;编写HAL库的按键检测代码五、运行仿真程序&#xff0c;调试代码 一、功能需求分析 搭建完成开发STM32开发环境之后&#xff0c;开始GPIO…
阅读更多...
OpenCv —— cv::VideoCapture设置摄像头图像格式为“MJPEG“

OpenCv —— cv::VideoCapture设置摄像头图像格式为“MJPEG“

背景 今天恰巧同事有台USB摄像头，她想要在Windows系统下通过OpenCV读取该摄像头宽高为1080x768、帧率为60的视频，用来做图像算法处理。但无奈通过网上OpenCV教程 读取的视频对应尺寸的帧率仅为10帧左右，根本无法满足使用要求。于是作者通过本篇文章介绍如何解决，欢迎交流指…
阅读更多...
0基础学习Mybatis系列数据库操作框架——多环境配置

0基础学习Mybatis系列数据库操作框架——多环境配置

大纲 配置代码参考资料 在实际开发中&#xff0c;我们往往会将开发环境分成&#xff1a;开发、测试、线上等环境。这些环境的数据源不一样&#xff0c;比如开发环境就不能访问线上环境&#xff0c;否则极容易出现线上数据污染等问题。Mybatis通过多环境配置分开定义来解决这个问…
阅读更多...
python核心篇之网络通信

python核心篇之网络通信

一. 发送请求 1. 发送get请求 2. 发送post请求 3. json数据与python数据的对应关系
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023