目录
- 1. 栈的概念
- 2. 栈的实现
- 2.1 顺序栈
- 2.2 链式栈
- 3. 栈的应用
- 3.1 栈的使用
- 3.2 括号匹配
- 3.3 逆波兰表达式求值
- 3.4 出栈入栈次序匹配
- 3.4 最小栈
1. 栈的概念
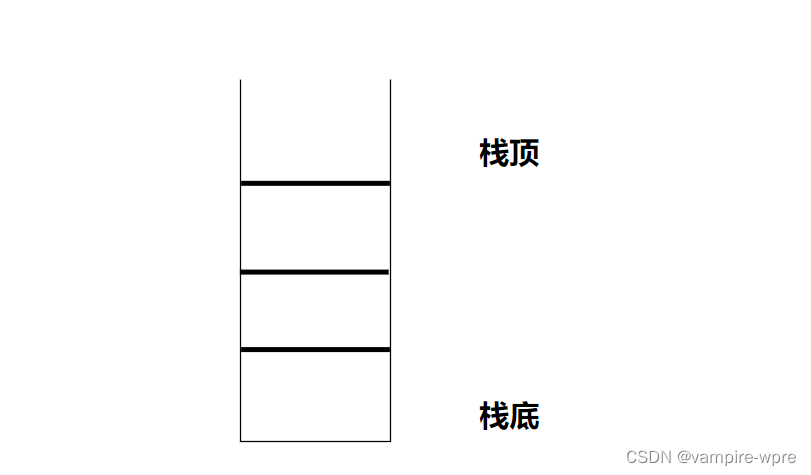
栈是一种顺序结构,只允许在一端进行插入和删除,插入删除的一端叫栈顶,另一端叫栈底。栈是一种先进后出(后进先出)的数据结构。插入数据的操作叫入栈,删除数据的操作叫出栈。
2. 栈的实现
栈的实现有两种,一种是顺序栈,底层是数组;另一种是链式栈,是用链表实现的。栈的主要功能有:push(入栈)、pop(出栈)、peek(获取栈顶元素,不删除)、empty(判断栈是否为空)
2.1 顺序栈
使用数组实现,定义curSize记录当前数据的个数,如果空间满了,通过copyOf方法扩容
public class myStack<E> {
public Object[] arr;//存放数据的数组
public int curSize;//当前数据的个数
public myStack() {
this.arr = new Object[10];
}
//入栈
public E push(E val) {
//满了,扩容
if (curSize == arr.length) {
this.arr = Arrays.copyOf(this.arr, 2 * this.arr.length);
}
arr[curSize] = val;
curSize++;
return val;//返回入栈的元素
}
//出栈
public E pop() {
if (empty()) {
//如果栈中为空
return null;
}
Object ret = this.arr[curSize - 1];
curSize--;
return (E) ret;//返回出栈的元素
}
//获取栈顶元素,不删除
public E peek() {
if (curSize == 0) {
return null;
}
Object ret = this.arr[curSize - 1];
return (E) ret;//返回栈顶元素
}
//判断是否为空
public boolean empty() {
return curSize == 0;
}
}
2.2 链式栈
如果用单链表实现栈,只能在链表的头部进行操作,这样时间复杂度才为O(1);如果使用的是双向链表,头部和尾部都可以,这里我们使用单链表实现
public class myStack<E> {
//链表的结点
static class ListNode {
public Object val;//数据
public ListNode next;//下一个结点
public ListNode(Object val) {
this.val = val;
}
}
public ListNode head;//(头结点)第一个结点
//入栈
public E push(E val) {
ListNode newNode = new ListNode(val);
if (head != null) {
newNode.next = head;
}
head = newNode;
return val;
}
//出栈
public E pop() {
if (head == null) {
return null;
}
Object ret = head.val;
if (head.next == null) {
head = null;
return (E) ret;
}
head = head.next;
return (E) ret;
}
//获取栈顶元素
public E peek() {
if (head == null) {
return null;
}
return (E) head.val;
}
//判断栈是否为空
public boolean empty() {
if (head == null) {
return true;
}
return true;
}
}
3. 栈的应用
3.1 栈的使用
在Java中,stack继承于Vector,实现了List接口
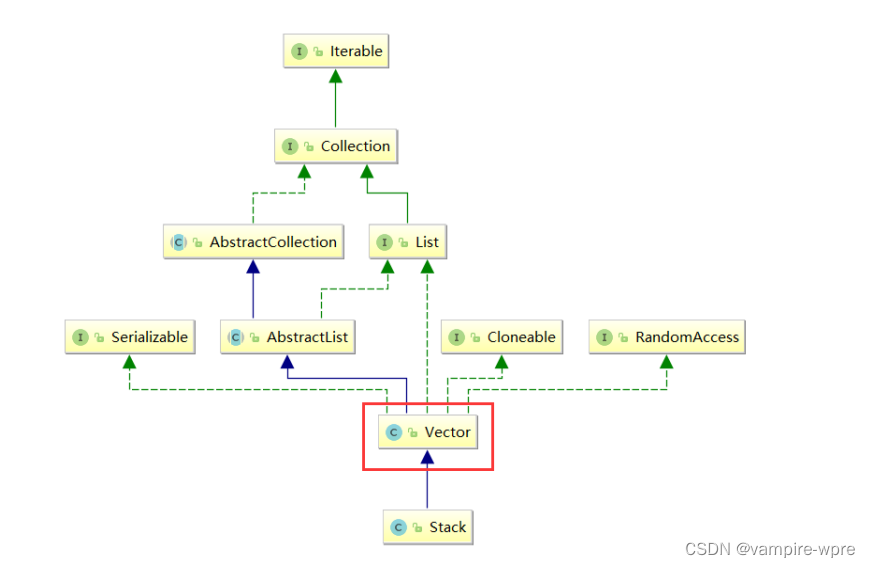
Java中stack的方法如下

search返回栈中某个元素举例栈顶的距离,如果该元素就是栈顶元素返回1,如果栈中不包含该元素,返回-1,如图
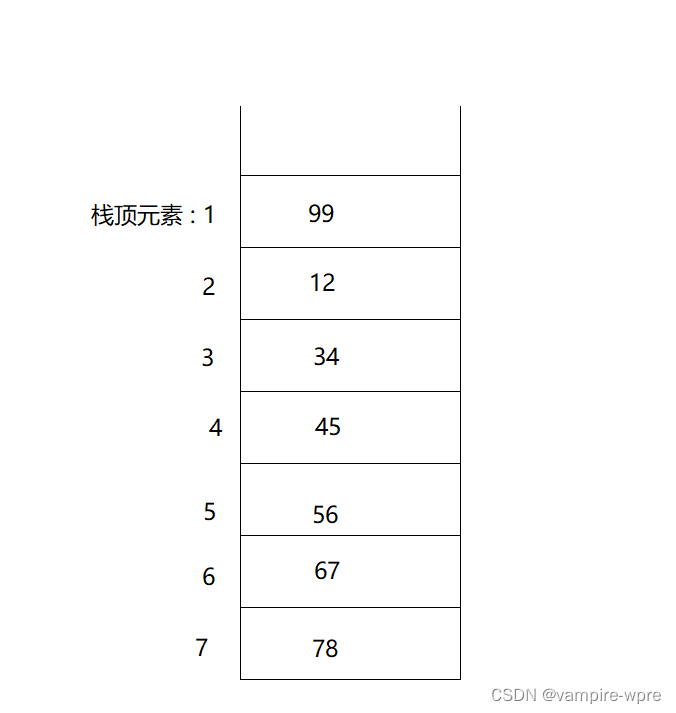
3.2 括号匹配

题目链接:有效的括号
题目要求: 给定字符串,字符串中只包含(){ } [ ],判断字符串中的括号是否能够匹配成功
解题思路: 遍历字符串,如果该字符是左括号就入栈,如果是右括号,看当前栈顶的元素是否与它匹配,如果匹配则将栈顶元素出栈;如果不匹配说明整个字符串都不匹配,此时返回false
匹配成功的条件是:字符串遍历结束并且栈为空

代码:
class Solution {
public boolean isValid(String s) {
Stack<Character> stack = new Stack<>();//创建字符类型的栈
for (int i = 0; i < s.length(); i++) {
char ch = s.charAt(i);//获取i下标的字符
if (ch == '(' || ch == '{' || ch == '[') {
//如果是左括号,入栈
stack.push(ch);
} else {
//i下标是右括号
//栈为空,返回
if (stack.empty()) {
return false;
}
//判断栈顶元素是否匹配
char tmp = stack.peek();
if (tmp == '(' && ch == ')' || tmp == '{' && ch == '}' || tmp == '[' && ch == ']') {
stack.pop();
} else {
return false;
}
}
}
return stack.empty();
}
}
3.3 逆波兰表达式求值

题目链接:逆波兰表达式求值
题目要求: 给定的字符串数组是逆波兰表达式,求逆波兰表达式的值
逆波兰表达式:(Reverse Polish Notation,RPN,或逆波兰记法),也叫后缀表达式(将运算符写在操作数之后),而中缀表达式就是我们平时看见的表达式,如何将中缀表达式转换为后缀表达式?分为两步
1.加括号:将表达式从左到右加括号(先乘除后加减)
2.移运算符:将括号内的运算符移到对应的括号外

解题思路: 要求逆波兰表达式的值,可以利用栈,申请一个栈,遍历字符串数组,如果是数字,则入栈,如果是操作符,出栈两个元素进行运算,先出栈的作为右操作数,后出栈的作为左操作数,将运算结果入栈。重复以上操作,当遍历完字符串数组时,此时栈内只剩下一个元素,该元素就是计算结果。
代码:
class Solution {
public int evalRPN(String[] tokens) {
Stack<Integer> stack = new Stack<>();
for (int i = 0; i < tokens.length; i++) {
String tmp = tokens[i];
if (!isOperation(tmp)) {
//如果不是操作符
Integer val = Integer.valueOf(tmp);//将字符转换为整型数字
stack.push(val);
} else {
Integer val2 = stack.pop();
Integer val1 = stack.pop();
switch (tmp) {
case "+":
stack.push(val1 + val2);
break;
case "-":
stack.push(val1 - val2);
break;
case "*":
stack.push(val1 * val2);
break;
case "/":
stack.push(val1 / val2);
break;
}
}
}
return stack.pop();
}
// 判断是否为操作符
public boolean isOperation(String s) {
if (s.equals("+") || s.equals("-") || s.equals("*") || s.equals("/")) {
return true;
}
return false;
}
}
3.4 出栈入栈次序匹配
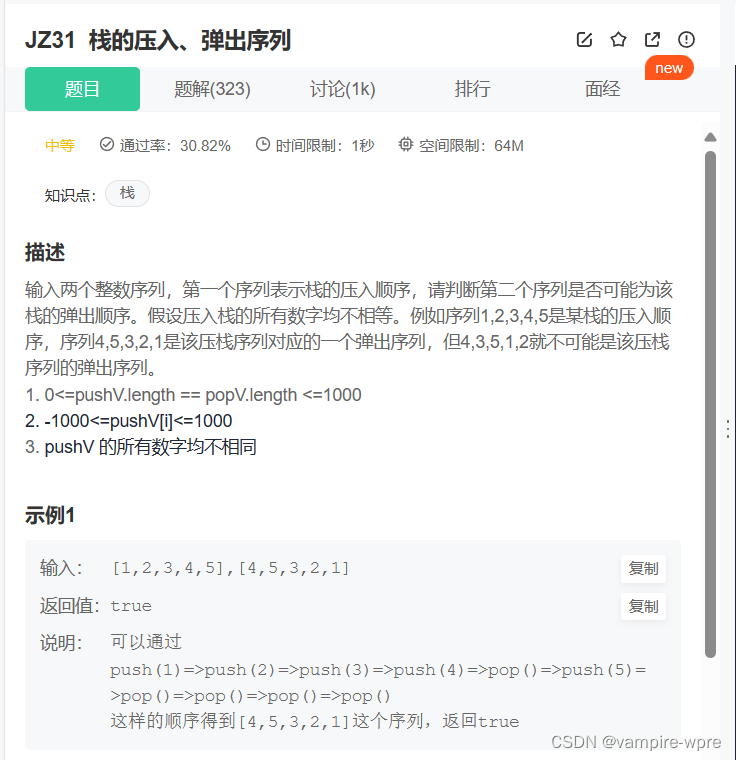
题目链接: 出入栈次序匹配
题目要求: 给定pushV数组,表示入栈的顺序,判断popV数组是否可能为出栈的顺序
解题思路: 申请一个栈,遍历pushV数组,同时定义下标j用于遍历popV数组,依次将pushV的元素入栈,每入栈一个元素,判断该元素是否与popV的元素相等,如果相等,弹出栈顶元素,j++,否则pushV继续入栈,如果popV的元素一直与栈顶元素相等,则一直出栈,当遍历完pushV数组后,栈此时为空说明次序匹配,如果不为空说明不匹配。
代码:
public boolean IsPopOrder(int[] pushV, int[] popV) {
// write code here
Stack<Integer> stack = new Stack<>();
int j = 0;//遍历popv
for (int i = 0; i < pushV.length; i++) {
stack.push(pushV[i]);//先入栈,再判断
while (j < popV.length && !stack.empty() && popV[j] == stack.peek()) {
//j不能越界,并且栈不为空
stack.pop();
j++;
}
}
return stack.empty();//判断最后的栈是不是空
}
3.4 最小栈

题目链接: 最小栈
题目要求: 设计一个支持插入(push)、删除(pop)、获取栈顶元素(top)、getMin获取栈中最小元素,getMin的时间复杂度为O(1)
解题思路: 创建两个栈,一个为普通的栈,另一个为最小栈,最小栈的栈顶元素既为普通栈的最小值。入栈: 普通栈正常入栈,最小栈需判断入栈的值是否比最小栈的栈顶元素小,如果小于或者等于则入栈(如果最小栈为空则直接入栈)。出栈: 判断普通栈出栈的元素是否与最小栈的栈顶元素相等,如果相等最小栈也要出栈
代码:
class MinStack {
public Stack<Integer> stack;
public Stack<Integer> Min;
public MinStack() {
stack = new Stack<>();
Min = new Stack<>();
}
public void push(int val) {
stack.push(val);
if (Min.empty() || val <= Min.peek()) {
Min.push(val);
}
}
public void pop() {
if (Min.peek().equals(stack.peek())) {
Min.pop();
stack.pop();
} else {
stack.pop();
}
}
public int top() {
if (stack.empty()) {
return -1;
}
return stack.peek();
}
public int getMin() {
return Min.peek();
}
}
**今天的内容就到这里,感谢老铁们的点赞、收藏、评论~❤ **