一、介绍
1.1 什么是算法
算法(Algorithm)是指解题方案的准确而完整的描述,是一系列解决问题的清晰指令,算法代表着用系统的方法描述解决问题的策略机制。也就是说,能够对一定规范的输入,在有限时间内获得所要求的输出。如果一个算法有缺陷,或不适合于某个问题,执行这个算法将不会解决这个问题。不同的算法可能用不同的时间,空间或效率来完成同样的任务。一个算法的优劣可以用空间复杂度与时间复杂度来衡量。
1.2 什么是数据结构
数据结构是计算机存储、组织数据的方式。数据结构是指相互之间存在一种或多种特定关系的数据元素的集合。通常情况下,精心选择的数据结构可以带来更高的运行或者存储效率。数据结构往往同高效的检索算法和索引技术有关。
二、复杂度
2.1 时间复杂度
在计算机科学中,时间复杂性,又称时间复杂度,算法的时间复杂度是一个函数,它定性描述该算法的运行时间。这是一个代表算法输入值的字符串的长度的函数。时间复杂度常用大 O 符号表述,不包括这个函数的低阶项和首项系数。使用这种方式时,时间复杂度可被称为是渐近的,亦即考察输入值大小趋近无穷时的情况。
2.2 空间复杂度
空间复杂度(Space Complexity)是对一个算法在运行过程中临时占用存储空间大小的量度,记做 S(n)=O(f(n))。比如直接插入排序的时间复杂度是 O(n^2),空间复杂度是 O(1) 。而一般的递归算法就要有 O(n)的空间复杂度了,因为每次递归都要存储返回信息。
三、链表
3.1 线性表
数组是一种连续存储线性结构,元素类型相同,大小相等。
线性表是最基本、最简单、也是最常用的一种数据结构。线性表(linear list)是数据结构的一种,一个线性表是 n 个具有相同特性的数据元素的有限序列。
3.1.1 数组
数组的定义
- 数组是相同类型数据的有序集合。
- 数组描述的是相同类型的若干个数据,按照一定的先后次序排列组合而成。
- 其中,每一个数据称作一个数组元素,每个数组元素可以通过一个下标来访问它们。
声明与创建
- 首先必须声明数组变量,才能在程序中使用数组。下面是声明数组变量的语法:
dataType[] arrayRefVar; //首选的方法
// 或
dataType arrayRefVar[]; //效果相同,但不是首选方法
- Java 语言使用 new 操作符来创建数组,语法如下:
dataType[ ] arrayRefVar = new dataType[ arraySize];
- 数组的元素是通过索引访问的,数组索引从 0 开始。
- 获取数组长度:
arrays.length
基本特点
- 其长度是确定的。数组一旦被创建,它的大小就是不可以改变的。
- 其元素必须是相同类型,不允许出现混合类型。
- 数组中的元素可以是任何数据类型,包括基本类型和引用类型。
- 数组变量属引用类型,数组也可以看成是对象,数组中的每个元素相当于该对象的成员变量。数组本身就是对象,Java 中对象是在堆中的,因此数组无论保存原始类型还是其他对象类型,数组对象本身是在堆中的。
数组的优点:
存取速度快。
数组的缺点:
事先必须知道数组的长度。
插入删除元素很慢。
空间通常是有限制的。
需要大块连续的内存块。
插入删除元素的效率很低。
初始化
- 静态初始化
int[] a = {1,2,3};
Man[ ] mans = {new Man(1,1),new Man(2,2)};
- 动态初始化
int[] a = new int[2];
a[0]=1;
a[1]=2;
- 默认初始化
数组是引用类型,它的元素相当于类的实例变量,因此数组一经分配空间,其中的每个元素也被按照实例变量同样的方式被隐式初始化。
内存分析
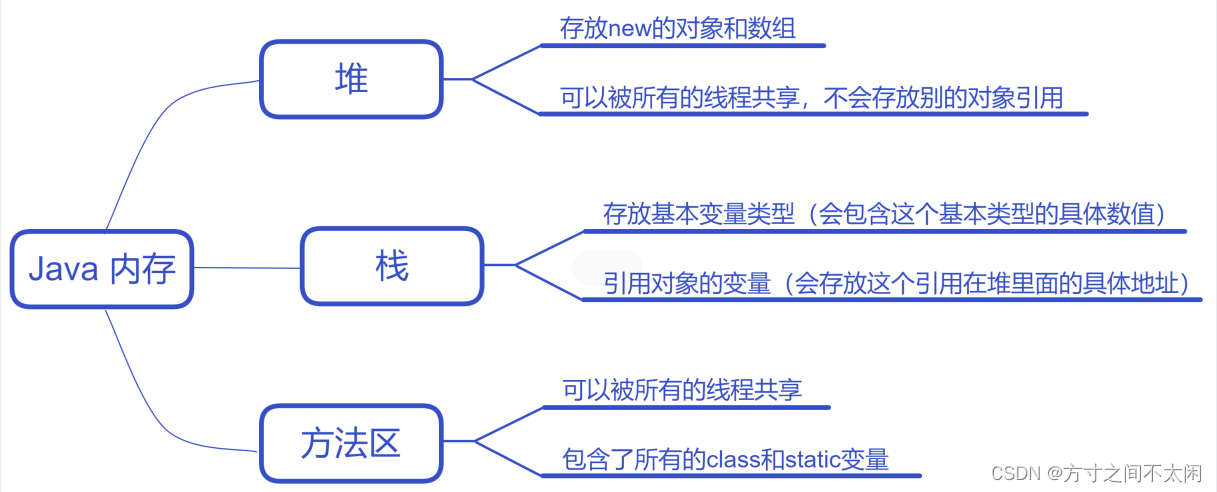
3.2 ArrayList 的底层分析
ArrayList 类封装了一个动态的、允许再分配的 Object[] 数组,这个对象表明可以接收任何类型的数据,ArrayList 对象使用 initCapacity 参数来设置该数组的长度,当向 ArrayList 集合中添加数据元素超过了该数组的长度时,它们的 initCapacity 会自动增加。自动增加的过程就是 ArrayList 扩容机制,底层实现是使用一个新的数组,将原数组的内容拷贝到新的数组中,并覆盖原有的数长度组的。扩容的长度是原来长度的 1.5 倍。是线程不安全的。
3.2.1 继承关系
java.lang.Object
|java.util.AbstractCollection<E>
|java.util.AbstractList<E>
|java.util.ArrayList<E> 3.2.2 部分源码
public class ArrayList<E> extends AbstractList<E>
implements List<E>, RandomAccess, Cloneable, java.io.Serializable {
//可序列化版本号
private static final long serialVersionUID = 8683452581122892189L;
//默认的初始化数组大小 为10 .
private static final int DEFAULT_CAPACITY = 10;
//实例化一个空数组
private static final Object[] EMPTY_ELEMENTDATA = {};
//存放List元素的数组
private transient Object[] elementData;
//List中元素的数量,和存放List元素的数组长度可能相等,也可能不相等
private int size;
//构造方法,指定初始化的数组长度
public ArrayList(int initialCapacity) {
super();
if (initialCapacity < 0)
throw new IllegalArgumentException("Illegal Capacity: "+
initialCapacity);
this.elementData = new Object[initialCapacity];
}
//无参构造方法
public ArrayList() {
super();
this.elementData = EMPTY_ELEMENTDATA;
}
//构造方法,参数为集合元素
public ArrayList(Collection<? extends E> c) {
//将集合转换成数组,并赋值给elementData数组
elementData = c.toArray();
size = elementData.length;
//如果c.toArray返回的不是Object[]类型的数组,转换成Object[]类型
if (elementData.getClass() != Object[].class)
elementData = Arrays.copyOf(elementData, size, Object[].class);
}
//改变数组的长度,使长度和List的size相等。
public void trimToSize() {
modCount++;
if (size < elementData.length) {
elementData = Arrays.copyOf(elementData, size);
}
}
//确定ArrayList的容量
//判断当前elementData是否是EMPTY_ELEMENTDATA,若是设置长度为10
public void ensureCapacity(int minCapacity) {
int minExpand = (elementData != EMPTY_ELEMENTDATA)
// any size if real element table
? 0
// larger than default for empty table. It's already supposed to be
// at default size.
: DEFAULT_CAPACITY;
//是否需要扩容
if (minCapacity > minExpand) {
ensureExplicitCapacity(minCapacity);
}
}
//当前位置和默认大小之间取最大值
private void ensureCapacityInternal(int minCapacity) {
if (elementData == EMPTY_ELEMENTDATA) {
minCapacity = Math.max(DEFAULT_CAPACITY, minCapacity);
}
ensureExplicitCapacity(minCapacity);
}
private void ensureExplicitCapacity(int minCapacity) {
modCount++;
// overflow-conscious code
if (minCapacity - elementData.length > 0)
grow(minCapacity);
}
//数组的最大容量
private static final int MAX_ARRAY_SIZE = Integer.MAX_VALUE - 8;
//扩容操作
private void grow(int minCapacity) {
// overflow-conscious code
int oldCapacity = elementData.length;
//容量扩充1.5倍
int newCapacity = oldCapacity + (oldCapacity >> 1);
if (newCapacity - minCapacity < 0)
newCapacity = minCapacity;
if (newCapacity - MAX_ARRAY_SIZE > 0)
newCapacity = hugeCapacity(minCapacity);
// minCapacity is usually close to size, so this is a win:
//生成一个长度为newCapacity数组,并将elementData数组中元素拷贝到新数组中,并将新数组的引用赋值给elementData
elementData = Arrays.copyOf(elementData, newCapacity);
}
private static int hugeCapacity(int minCapacity) {
if (minCapacity < 0) // overflow
throw new OutOfMemoryError();
return (minCapacity > MAX_ARRAY_SIZE) ?
Integer.MAX_VALUE :
MAX_ARRAY_SIZE;
}
//返回数组中已经放入的元素个数,非数组长度
public int size() {
return size;
}
//List是否为空
public boolean isEmpty() {
return size == 0;
}
//判断是否包包含指定元素
public boolean contains(Object o) {
return indexOf(o) >= 0;
}
//查找指定的元素,存在返回下标,不存在放回 -1
public int indexOf(Object o) {
if (o == null) {
for (int i = 0; i < size; i++)
if (elementData[i]==null)
return i;
} else {
for (int i = 0; i < size; i++)
if (o.equals(elementData[i]))
return i;
}
return -1;
}
//倒序查找元素,存在放回下标,不存在返回-1
public int lastIndexOf(Object o) {
if (o == null) {
for (int i = size-1; i >= 0; i--)
if (elementData[i]==null)
return i;
} else {
for (int i = size-1; i >= 0; i--)
if (o.equals(elementData[i]))
return i;
}
return -1;
}
//因为实现了clone接口,所以需要重写clone()方法,实现对象的拷贝
public Object clone() {
try {
@SuppressWarnings("unchecked")
ArrayList<E> v = (ArrayList<E>) super.clone();
v.elementData = Arrays.copyOf(elementData, size);
v.modCount = 0;
return v;
} catch (CloneNotSupportedException e) {
// this shouldn't happen, since we are Cloneable
throw new InternalError();
}
}
//将集合转化为数组
public Object[] toArray() {
return Arrays.copyOf(elementData, size);
}
//转化为指定类型的数组元素,推荐使用此方法
@SuppressWarnings("unchecked")
public <T> T[] toArray(T[] a) {
if (a.length < size)
// Make a new array of a's runtime type, but my contents:
return (T[]) Arrays.copyOf(elementData, size, a.getClass());
System.arraycopy(elementData, 0, a, 0, size);
if (a.length > size)
a[size] = null;
return a;
}
// Positional Access Operations
//放回指定位置的数组元素
@SuppressWarnings("unchecked")
E elementData(int index) {
return (E) elementData[index];
}
//返回列表中指定位置的元素
public E get(int index) {
rangeCheck(index);
return elementData(index);
}
//设置指定位置的元素,并返回被替换的元素
public E set(int index, E element) {
rangeCheck(index);
E oldValue = elementData(index);
elementData[index] = element;
return oldValue;
}
//添加元素
public boolean add(E e) {
ensureCapacityInternal(size + 1); // Increments modCount!!
elementData[size++] = e;
return true;
}
//将元素添加到指定位置上,从指定位置的元素开始所有元素向后移动,为新添加的元素提供位置
public void add(int index, E element) {
rangeCheckForAdd(index);
ensureCapacityInternal(size + 1); // Increments modCount!!
System.arraycopy(elementData, index, elementData, index + 1,
size - index);
elementData[index] = element;
size++;
}
//删除指定位置的元素,其他元素做相依的移动,并将最后一个元素置空,方便垃圾处理机制回收,防止内存泄露,并返回删除的元素值
public E remove(int index) {
rangeCheck(index);
modCount++;
E oldValue = elementData(index);
int numMoved = size - index - 1;
if (numMoved > 0)
System.arraycopy(elementData, index+1, elementData, index,
numMoved);
elementData[--size] = null; // clear to let GC do its work
return oldValue;
}
//删除元素方法
public boolean remove(Object o) {
if (o == null) {
for (int index = 0; index < size; index++)
if (elementData[index] == null) {
fastRemove(index);
return true;
}
} else {
for (int index = 0; index < size; index++)
if (o.equals(elementData[index])) {
fastRemove(index);
return true;
}
}
return false;
}
//快速删除执行操作
private void fastRemove(int index) {
modCount++;
int numMoved = size - index - 1;
if (numMoved > 0)
System.arraycopy(elementData, index+1, elementData, index,
numMoved);
elementData[--size] = null; // clear to let GC do its work
}
//清除列表
public void clear() {
modCount++;
// clear to let GC do its work
for (int i = 0; i < size; i++)
elementData[i] = null;
size = 0;
}
//添加方法,添加的元素为集合
public boolean addAll(Collection<? extends E> c) {
Object[] a = c.toArray();
int numNew = a.length;
ensureCapacityInternal(size + numNew); // Increments modCount
System.arraycopy(a, 0, elementData, size, numNew);
size += numNew;
return numNew != 0;
}
//从指定位置开始添加集合元素
public boolean addAll(int index, Collection<? extends E> c) {
rangeCheckForAdd(index);
Object[] a = c.toArray();
int numNew = a.length;
ensureCapacityInternal(size + numNew); // Increments modCount
int numMoved = size - index;
if (numMoved > 0)
System.arraycopy(elementData, index, elementData, index + numNew,
numMoved);
System.arraycopy(a, 0, elementData, index, numNew);
size += numNew;
return numNew != 0;
}
//范围删除方法
protected void removeRange(int fromIndex, int toIndex) {
modCount++;
int numMoved = size - toIndex;
System.arraycopy(elementData, toIndex, elementData, fromIndex,
numMoved);
// clear to let GC do its work
int newSize = size - (toIndex-fromIndex);
for (int i = newSize; i < size; i++) {
elementData[i] = null;
}
size = newSize;
}
//下标检测方法,如果不合法,抛出IndexOutOfBoundsException异常
private void rangeCheck(int index) {
if (index >= size)
throw new IndexOutOfBoundsException(outOfBoundsMsg(index));
}
/**
* A version of rangeCheck used by add and addAll.
*/
private void rangeCheckForAdd(int index) {
if (index > size || index < 0)
throw new IndexOutOfBoundsException(outOfBoundsMsg(index));
}
//溢出信息
private String outOfBoundsMsg(int index) {
return "Index: "+index+", Size: "+size;
}
//删除所有元素
public boolean removeAll(Collection<?> c) {
return batchRemove(c, false);
}
public boolean retainAll(Collection<?> c) {
return batchRemove(c, true);
}
private boolean batchRemove(Collection<?> c, boolean complement) {
final Object[] elementData = this.elementData;
int r = 0, w = 0;
boolean modified = false;
try {
for (; r < size; r++)
if (c.contains(elementData[r]) == complement)
elementData[w++] = elementData[r];
} finally {
// Preserve behavioral compatibility with AbstractCollection,
// even if c.contains() throws.
if (r != size) {
System.arraycopy(elementData, r,
elementData, w,
size - r);
w += size - r;
}
if (w != size) {
// clear to let GC do its work
for (int i = w; i < size; i++)
elementData[i] = null;
modCount += size - w;
size = w;
modified = true;
}
}
return modified;
}
//流操作方法,将对象写入输出流中
private void writeObject(java.io.ObjectOutputStream s)
throws java.io.IOException{
// Write out element count, and any hidden stuff
int expectedModCount = modCount;
s.defaultWriteObject();
// Write out size as capacity for behavioural compatibility with clone()
s.writeInt(size);
// Write out all elements in the proper order.
for (int i=0; i<size; i++) {
s.writeObject(elementData[i]);
}
if (modCount != expectedModCount) {
throw new ConcurrentModificationException();
}
}
//流操作,读方法,将对象从流中取出
private void readObject(java.io.ObjectInputStream s)
throws java.io.IOException, ClassNotFoundException {
elementData = EMPTY_ELEMENTDATA;
// Read in size, and any hidden stuff
s.defaultReadObject();
// Read in capacity
s.readInt(); // ignored
if (size > 0) {
// be like clone(), allocate array based upon size not capacity
ensureCapacityInternal(size);
Object[] a = elementData;
// Read in all elements in the proper order.
for (int i=0; i<size; i++) {
a[i] = s.readObject();
}
}
}
//迭代方法,返回内部类实例
public ListIterator<E> listIterator(int index) {
if (index < 0 || index > size)
throw new IndexOutOfBoundsException("Index: "+index);
return new ListItr(index);
}
//迭代方法,返回内部类实例
public ListIterator<E> listIterator() {
return new ListItr(0);
}
//迭代方法,返回内部类实例
public Iterator<E> iterator() {
return new Itr();
}
//内部类,实现Iterator接口
private class Itr implements Iterator<E> {
int cursor; // index of next element to return
int lastRet = -1; // index of last element returned; -1 if no such
int expectedModCount = modCount;
//是否还有下一个元素,返回true or false
public boolean hasNext() {
return cursor != size;
}
//返回元素
@SuppressWarnings("unchecked")
public E next() {
checkForComodification();
int i = cursor;
if (i >= size)
throw new NoSuchElementException();
Object[] elementData = ArrayList.this.elementData; //获取外部类的elementData数组
if (i >= elementData.length)
throw new ConcurrentModificationException();
cursor = i + 1;
return (E) elementData[lastRet = i];
}
//删除元素
public void remove() {
if (lastRet < 0)
throw new IllegalStateException();
checkForComodification();
try {
ArrayList.this.remove(lastRet); //调用外部类删除方法,删除指定位置的元素
cursor = lastRet;
lastRet = -1;
expectedModCount = modCount;
} catch (IndexOutOfBoundsException ex) {
throw new ConcurrentModificationException();
}
}
final void checkForComodification() {
if (modCount != expectedModCount)
throw new ConcurrentModificationException();
}
}
//省略了ListItr、SubList两个内部类
}3.2.3 构造方法
ArrayList(int initialCapacity);
ArrayList();
ArrayList(Collection<? extends E> c);
上面是 ArrayList 的三个构造方法,使用三种方法都可以创建一个 ArrayList 集合,但是它们还是有一些区别:
- 使用第一个构造方法, 直接创建了指定大小的 Object[] 数组来创建集合。
- 使用第二个构造方法,创建的是一个空的数组,是将一个已经创建好的,使用 static final 修饰的数组的引用赋值给了 elementData ,此时的长度为零,当添加元素时, elementData = Arrays.copyOf(elementData, newCapacity);完成了 elementData 新的初始化工作,此时的长度才为 10。
- 第三种构造方法是将集合转化为 ArrayList ,在底层实现中,先调用集合的 toArray() 方法,并赋值给 elementData, 然后进行类型的判断,是如果类型不是 Object[] 类型,那么将使用反射生成一个 Object[] 的数组,并重新赋值给 elementData。
3.2.4 扩容机制
数组的特点是:一旦创建,容量无法改变。所以在往数组中添加指定元素之前,应该考虑数组容量空间是否已满,如果再进行数据的插入时,数组已满,则必须对其进行扩容操作。扩容操作的实质就是创建一个容量更大的新数组,再将旧数组的元素复制到新数组中去。这里以 ArrayList 的 添加操作为例,来看下 ArrayList 内部数组扩容的过程。
public boolean add(E e) {
// 关键 -> 添加之前,校验容量
ensureCapacityInternal(size + 1);
// 修改 size,并在数组末尾添加指定元素
elementData[size++] = e;
return true;
}
// 关键 -> minCapacity = size+1,即表示执行完添加操作后,数组中的元素个数
private void ensureCapacityInternal(int minCapacity) {
// 判断内部数组是否为空
if (elementData == EMPTY_ELEMENTDATA) {
// 设置数组最小容量(>=10)
minCapacity = Math.max(DEFAULT_CAPACITY, minCapacity);
}
ensureExplicitCapacity(minCapacity);
}
//接着会判断添加操作会不会导致内部数组的容量饱和
private void ensureExplicitCapacity(int minCapacity) {
modCount++;
// 判断结果为 true,则表示接下来的添加操作会导致元素数量超出数组容量
if (minCapacity - elementData.length > 0){
// 真正的扩容操作
grow(minCapacity);
}
}
//实现真正的扩容公式与数组的拷贝
private static final int MAX_ARRAY_SIZE = Integer.MAX_VALUE - 8;
private void grow(int minCapacity) {
int oldCapacity = elementData.length;
// 关键-> 容量扩充公式
int newCapacity = oldCapacity + (oldCapacity >> 1);
// 针对新容量的一系列判断
if (newCapacity - minCapacity < 0){
newCapacity = minCapacity;
}
if (newCapacity - MAX_ARRAY_SIZE > 0){
newCapacity = hugeCapacity(minCapacity);
}
// 关键 -> 复制旧数组元素到新数组中去
elementData = Arrays.copyOf(elementData, newCapacity);
}
private static int hugeCapacity(int minCapacity) {
if (minCapacity < 0){
throw new OutOfMemoryError();
}
return (minCapacity > MAX_ARRAY_SIZE) ? Integer.MAX_VALUE : MAX_ARRAY_SIZE;
}
- ArrayList 是基于数组实现的 List 类。会自动扩容,采用 Array.copyOf() 实现。
- 如果在创建 ArrayList 时,可以知道 ArrayList 元素的数量最好指定初始容量,这样可以避免 ArrayList 的自动多次扩容问题。
3.3 链表
3.3.1 什么是链表
链表 [Linked List]:链表是由一组不必相连(不必相连:可以连续也可以不连续)的内存结构(节点),按特定的顺序链接在一起的抽象数据类型。
> 抽象数据类型(Abstract Data Type [ADT]):表示数学中抽象出来的一些操作的集合。
> 内存结构:内存中的结构,如:struct、特殊内存块…等等之类;
链表是离散存储线性结构
n 个节点离散分配,彼此通过指针相连,每个节点只有一个前驱节点,每个节点只有一 个后续节点,首节点没有前驱节点,尾节点没有后续节点。
链表优点: 空间没有限制 插入删除元素很快。
链表缺点: 存取速度很慢。
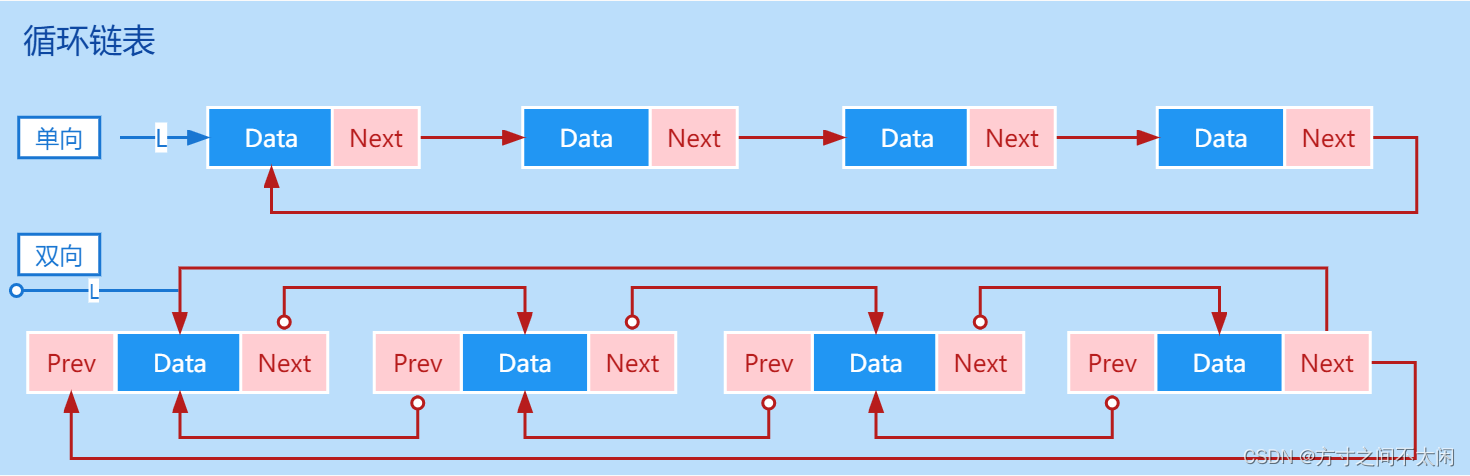
链表常用的有 3 类: 单链表、双向链表、循环链表。
- 单链表 [Linked List]:由各个内存结构通过一个 Next 指针链接在一起组成,每一个内存结构都存在后继内存结构(链尾除外),内存结构由数据域和 Next 指针域组成。

- 双向链表 [Double Linked List]:由各个内存结构通过指针 Next 和指针 Prev 链接在一起组成,每一个内存结构都存在前驱内存结构和后继内存结构(链头没有前驱,链尾没有后 继),内存结构由数据域、Prev 指针域和 Next 指针域组成。

- 单向循环链表 [Circular Linked List] : 由各个内存结构通过一个指针 Next 链接在一起组成,每一个内存结构都存在后继内存结构,内存结构由数据域和 Next 指针域组成。 双向循环链表 [Double Circular Linked List] : 由各个内存结构通过指针 Next 和指针 Prev 链接在一起组成,每一个内存结构都存在前驱内存结构和后继内存结构,内存结构由 数据域、Prev 指针域和 Next指针域组成。
四、二分查找
二分查找也称折半查找(Binary Search),它是一种效率较高的查找方法。但是,折半查找要求线性表必须采用顺序存储结构,而且表中元素按关键字有序排列。
4.1 查找过程
首先,假设表中元素是按升序排列,将表中间位置记录的关键字与查找关键字比较,如果两者相等,则查找成功;否则利用中间位置记录将表分成前、后两个子表,如果中间位置记录的关键字大于查找关键字,则进一步查找前一子表,否则进一步查找后一子表。重复以上过程,直到找到满足条件的记录,使查找成功,或直到子表不存在为止,此时查找不成功。
4.2 算法要求
1. 必须采用顺序存储结构。
2. 必须按关键字大小有序排列。
4.2 比较次数
计算公式:
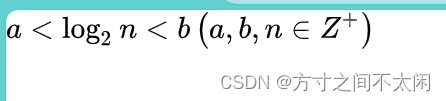
当顺序表有 n 个关键字时:
查找失败时,至少比较 a 次关键字;查找成功时,最多比较关键字次数是 b。
注意:a,b,n 均为正整数。
4.3 算法复杂度
二分查找的基本思想是将 n 个元素分成大致相等的两部分,取 a[n/2]与 x 做比较,如果 x=a[n/2],则找到 x,算法中止;如果 x<a[n/2],则只要在数组 a 的左半部分继续搜索 x,如果 x>a[n/2],则只要在数组 a 的右半部搜索 x。
时间复杂度即是 while 循环的次数。
总共有 n 个元素,渐渐跟下去就是 n,n/2,n/4,....n/2^k(接下来操作元素的剩余个数),其中 k 就是循环的次数。
由于你 n/2^k 取整后>=1
即令 n/2^k=1
可得 k=log2n,(是以 2 为底,n 的对数)
所以时间复杂度可以表示 O(h)=O(log2n)
public static int binarySearch(Integer[] srcArray, int des) {
//定义初始最小、最大索引
int start = 0;
int end = srcArray.length - 1;
//确保不会出现重复查找,越界
while (start <= end) {
//计算出中间索引值
int middle = (end + start)>>>1 ;//防止溢出
if (des == srcArray[middle]) {
return middle;
//判断下限
} else if (des < srcArray[middle]) {
end = middle - 1;
//判断上限
} else {
start = middle + 1;
}
}
//若没有,则返回-1
return -1;
}
折半查找法也称为二分查找法,它充分利用了元素间的次序关系,采用分治策略,可在最坏的情况下用O(log n)完成搜索任务。它的基本思想是:(这里假设数组元素呈升序排列)将 n 个元素分成个数大致相同的两半,取 a[n/2]与欲查找的 x 作比较,如果 x=a[n/2]则找到 x,算法终止;如 果 x<a[n/2],则我们只要在数组 a 的左半部继续搜索 x;如果 x>a[n/2],则我们只要在数组 a 的右 半部继续搜索 x。
五、排序
5.1 冒泡排序
每次循环都比较前后两个元素的大小,如果前者大于后者,则将两者进行交换。这样做会将每次循环中最大的元素替换到末尾,逐渐形成有序集合。将每次循环中的最大元素逐渐由队首转移到队尾的过程形似“冒泡”过程,故因此得名。一个优化冒泡排序的方法就是如果在一次循环的过程中没有发生交换,则可以立即退出当前循环,因为此时已经排好序了(也就是时间复杂度最好情况下是O(n)O(n)的由来)。
public int[] bubbleSort(int[] array) {
if (array == null || array.length < 2) {
return array;
}
for (int i = 0; i < array.length - 1; i++) {
boolean flag = false;
for (int j = 0; j < array.length - 1 - i; j++) {
if (array[j] > array[j + 1]) {
//这里交换两个数据并没有使用中间变量,而是使用异或的方式来实现
array[j] = array[j] ^ array[j + 1];
array[j + 1] = array[j] ^ array[j + 1];
array[j] = array[j] ^ array[j + 1];
flag = true;
}
}
if (!flag) {
break;
}
}
return array;
}
public class Demo {
public static void main(String[] args) {
int[] a = {7, 3, 5, 9, 4, 6, 8, 2, 1};
int iTmp = 0;
for(int i=0; i<a.length; i++) {
for(int j=0; j<a.length-i-1; j++) {
if(a[j] > a[j+1]) {
iTmp = a[j];
a[j] = a[j+1];
a[j+1] = iTmp;
}
}
}
for(int i=0; i<a.length; i++) {
System.out.println(a[i]);
}
}
}
5.2 选择排序
每次循环都会找出当前循环中最小的元素,然后和此次循环中的队首元素进行交换。
public int[] selectSort(int[] array) {
if (array == null || array.length < 2) {
return array;
}
for (int i = 0; i < array.length - 1; i++) {
int minIndex = i;
for (int j = i + 1; j < array.length; j++) {
if (array[j] < array[minIndex]) {
minIndex = j;
}
}
if (minIndex > i) {
array[i] = array[i] ^ array[minIndex];
array[minIndex] = array[i] ^ array[minIndex];
array[i] = array[i] ^ array[minIndex];
}
}
return array;
}5.3 插入排序
插入排序的精髓在于每次都会在先前排好序的子集合中插入下一个待排序的元素,每次都会判断待排序元素的上一个元素是否大于待排序元素,如果大于,则将元素右移,然后判断再上一个元素与待排序元素...以此类推。直到小于等于比较元素时就是找到了该元素的插入位置。这里的等于条件放在哪里很重要,因为它是决定插入排序稳定与否的关键。
public int[] insertSort(int[] array) {
if (array == null || array.length < 2) {
return array;
}
for (int i = 1; i < array.length; i++) {
int temp = array[i];
int j = i - 1;
while (j >= 0 && array[j] > temp) {
array[j + 1] = array[j];
j--;
}
array[j + 1] = temp;
}
return array;
}5.4 希尔排序
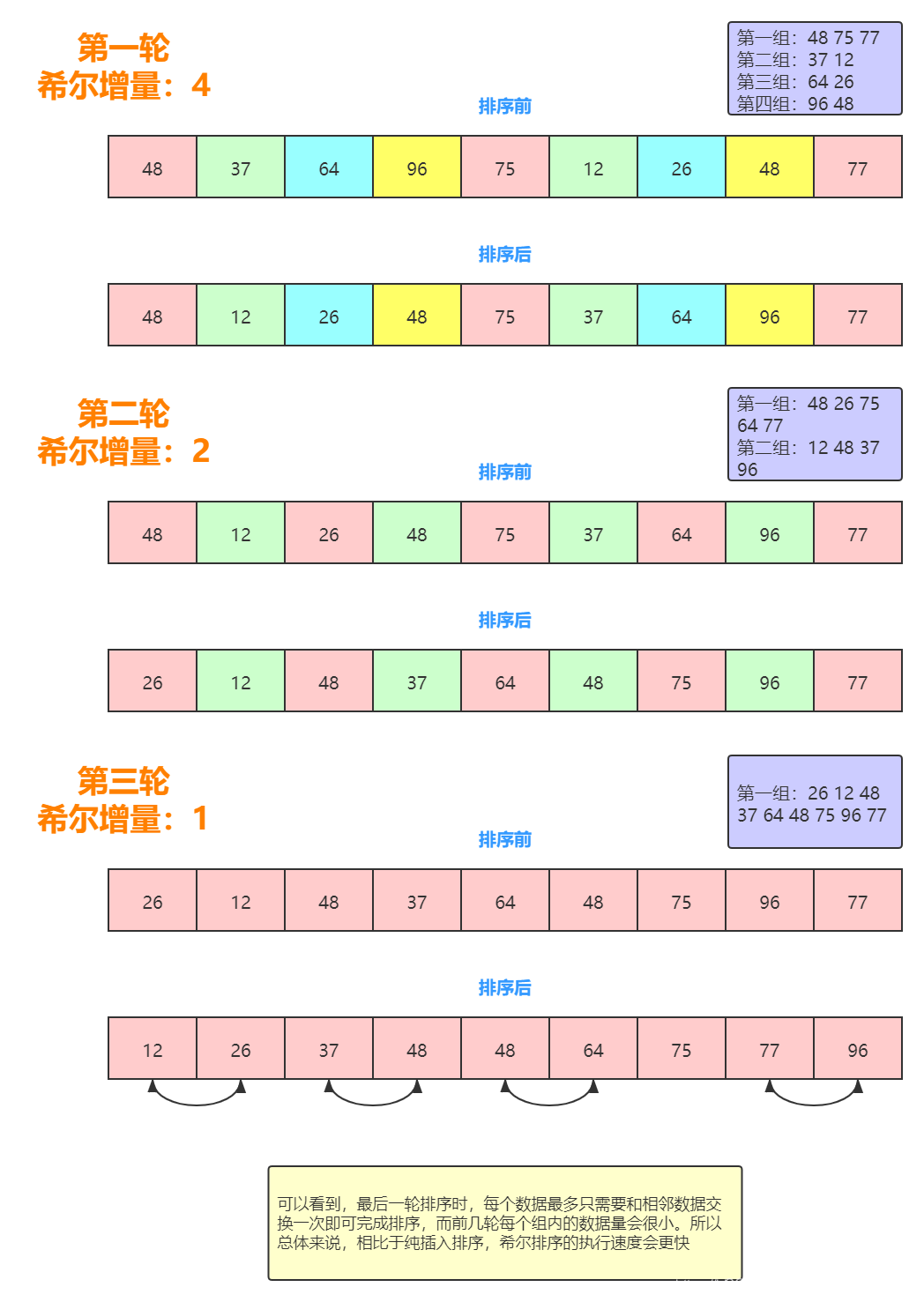
希尔排序可以认为是插入排序的改进版本。首先按照初始增量来将数组分成多个组,每个组内部使用插入排序。然后缩小增量来重新分组,组内再次使用插入排序...重复以上步骤,直到增量变为 1 的时候,这个时候整个数组就是一个分组,进行最后一次完整的插入排序即可结束。
在排序开始时的增量较大,分组也会较多,但是每个分组中的数据较少,所以插入排序会很快。随着每一轮排序的进行,增量和分组数会逐渐变小,每个分组中的数据会逐渐变多。但因为之前已经经过了多轮的分组排序,而此时的数组会趋近于一个有序的状态,所以这个时候的排序也是很快的。而对于数据较多且趋向于无序的数据来说,如果只是使用插入排序的话效率就并不高。所以总体来说,希尔排序的执行效率是要比插入排序高的。
public int[] shellSort(int[] array) {
if (array == null || array.length < 2) {
return array;
}
int gap = array.length >>> 1;
while (gap > 0) {
for (int i = gap; i < array.length; i++) {
int temp = array[i];
int j = i - gap;
while (j >= 0 && array[j] > temp) {
array[j + gap] = array[j];
j = j - gap;
}
array[j + gap] = temp;
}
gap >>>= 1;
}
return array;
}5.5 堆排序
堆排序的过程是首先构建一个大顶堆,大顶堆首先是一棵完全二叉树,其次它保证堆中某个节点的值总是不大于其父节点的值。
因为大顶堆中的最大元素肯定是根节点,所以每次取出根节点即为当前大顶堆中的最大元素,取出后剩下的节点再重新构建大顶堆,再取出根节点,再重新构建…
重复这个过程,直到数据都被取出,最后取出的结果即为排好序的结果。
public class MaxHeap {
/**
* 排序数组
*/
private int[] nodeArray;
/**
* 数组的真实大小
*/
private int size;
private int parent(int index) {
return (index - 1) >>> 1;
}
private int leftChild(int index) {
return (index << 1) + 1;
}
private int rightChild(int index) {
return (index << 1) + 2;
}
private void swap(int i, int j) {
nodeArray[i] = nodeArray[i] ^ nodeArray[j];
nodeArray[j] = nodeArray[i] ^ nodeArray[j];
nodeArray[i] = nodeArray[i] ^ nodeArray[j];
}
private void siftUp(int index) {
//如果index处节点的值大于其父节点的值,则交换两个节点值,同时将index指向其父节点,继续向上循环判断
while (index > 0 && nodeArray[index] > nodeArray[parent(index)]) {
swap(index, parent(index));
index = parent(index);
}
}
private void siftDown(int index) {
//左孩子的索引比size小,意味着索引index处的节点有左孩子,证明此时index节点不是叶子节点
while (leftChild(index) < size) {
//maxIndex记录的是index节点左右孩子中最大值的索引
int maxIndex = leftChild(index);
//右孩子的索引小于size意味着index节点含有右孩子
if (rightChild(index) < size && nodeArray[rightChild(index)] > nodeArray[maxIndex]) {
maxIndex = rightChild(index);
}
//如果index节点值比左右孩子值都大,则终止循环
if (nodeArray[index] >= nodeArray[maxIndex]) {
break;
}
//否则进行交换,将index指向其交换的左孩子或右孩子,继续向下循环,直到叶子节点
swap(index, maxIndex);
index = maxIndex;
}
}
private void add(int value) {
nodeArray[size++] = value;
//构建大顶堆
siftUp(size - 1);
}
private void extractMax() {
/*
将堆顶元素和最后一个元素进行交换
此时并没有删除元素,而只是将size-1,剩下的元素重新构建成大顶堆
*/
swap(0, --size);
//重新构建大顶堆
siftDown(0);
}
public int[] heapSort(int[] array) {
if (array == null || array.length < 2) {
return array;
}
nodeArray = new int[array.length];
for (int value : array) {
add(value);
}
for (int ignored : array) {
extractMax();
}
return nodeArray;
}
}
上面的经典实现中,如果需要变动节点时,都会来一次父子节点的互相交换操作(包括删除节点时首先做的要删除节点和最后一个节点之间的交换操作也是如此)。如果仔细思考的话,就会发现这其实是多余的。在需要交换节点的时候,只需要 siftUp 操作时的父节点或 siftDown 时的孩子节点重新移到当前需要比较的节点位置上,而比较节点是不需要移动到它们的位置上的。此时直接进入到下一次的判断中,重复 siftUp 或 siftDown 过程,直到最后找到了比较节点的插入位置后,才会将其插入进去。这样做的好处是可以省去一半的节点赋值的操作,提高了执行的效率。
5.6 归并排序
归并排序使用的是分治的思想,首先将数组不断拆分,直到最后拆分成两个元素的子数组,将这两个元素进行排序合并,再向上递归。不断重复这个拆分和合并的递归过程,最后得到的就是排好序的结果。
合并的过程是将两个指针指向两个子数组的首位元素,两个元素进行比较,较小的插入到一个 temp 数组中,同时将该数组的指针右移一位,继续比较该数组的第二个元素和另一个元素…重复这个过程。这样 temp 数组保存的便是这两个子数组排好序的结果。最后将 temp 数组复制回原数组的位置处即可。
public int[] mergeSort(int[] array) {
if (array == null || array.length < 2) {
return array;
}
return mergeSort(array, 0, array.length - 1);
}
private int[] mergeSort(int[] array, int left, int right) {
if (left < right) {
//这里没有选择“(left + right) / 2”的方式,是为了防止数据溢出
int mid = left + ((right - left) >>> 1);
// 拆分子数组
mergeSort(array, left, mid);
mergeSort(array, mid + 1, right);
// 对子数组进行合并
merge(array, left, mid, right);
}
return array;
}
private void merge(int[] array, int left, int mid, int right) {
int[] temp = new int[right - left + 1];
// p1和p2为需要对比的两个数组的指针,k为存放temp数组的指针
int p1 = left, p2 = mid + 1, k = 0;
while (p1 <= mid && p2 <= right) {
if (array[p1] <= array[p2]) {
temp[k++] = array[p1++];
} else {
temp[k++] = array[p2++];
}
}
// 把剩余的数组直接放到temp数组中
while (p1 <= mid) {
temp[k++] = array[p1++];
}
while (p2 <= right) {
temp[k++] = array[p2++];
}
// 复制回原数组
for (int i = 0; i < temp.length; i++) {
array[i + left] = temp[i];
}
}5.7 快速排序
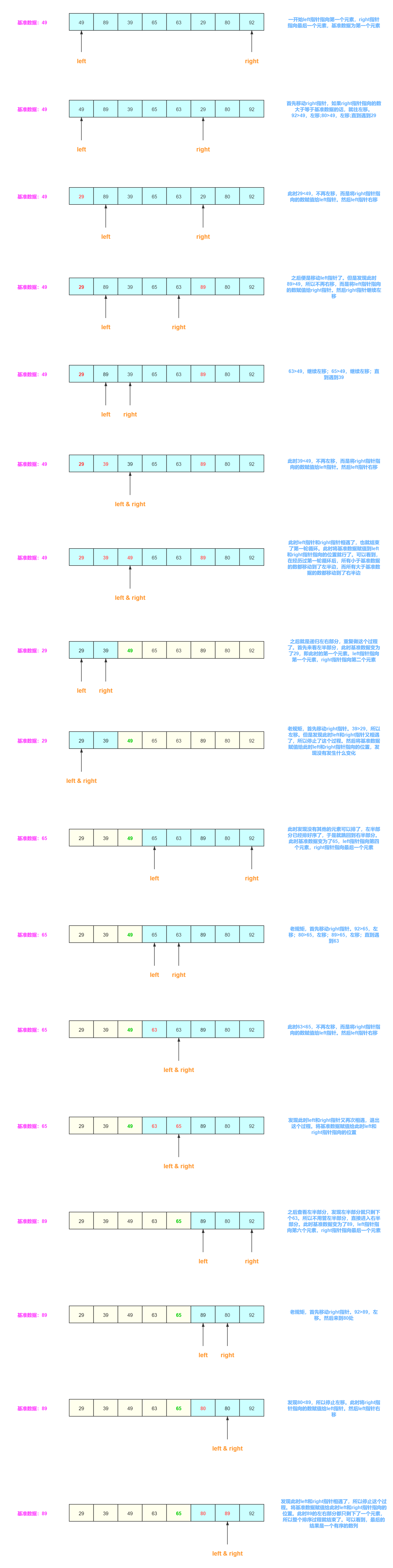
快速排序的核心是要有一个基准数据 temp,一般取数组的第一个位置元素。然后需要有两个指针 left 和 right,分别指向数组的第一个和最后一个元素。
首先从 right 开始,比较 right 位置元素和基准数据。如果大于等于,则将 right 指针左移,比较下一位元素;如果小于,就将 right 指针处数据赋给 left 指针处(此时 left 指针处数据已保存进 temp 中),left 指针+1,之后开始比较 left指针处数据。
拿 left 位置元素和基准数据进行比较。如果小于等于,则将 left 指针右移,比较下一位元素;而如果大于就将 left 指针处数据赋给 right 指针处,right 指针-1,之后开始比较 right 指针处数据…重复这个过程。
直到 left 和 right 指针相等时,说明这一次比较过程完成。此时将先前存放进 temp 中的基准数据赋值给当前 left 和 right 指针共同指向的位置处,即可完成这一次排序操作。
之后递归排序基础数据的左半部分和右半部分,递归的过程和上面讲述的过程是一样的,只不过数组范围不再是原来的全部数组了,而是现在的左半部分或右半部分。当全部的递归过程结束后,最终结果即为排好序的结果。
快速排序执行示意图:
正如上面所说的,一般取第一个元素作为基准数据,但如果当前数据为从大到小排列好的数据,而现在要按从小到大的顺序排列,则数据分摊不均匀,时间复杂度会退化为 O(n2)O(n2),而不是正常情况下的 O(nlog2n)O(nlog2n)。此时采取一个优化手段,即取最左边、最右边和最中间的三个元素的中间值作为基准数据,以此来避免时间复杂度为 O(n2)O(n2)的情况出现,当然也可以选择更多的锚点或者随机选择的方式来进行选取。
还有一个优化的方法是:像快速排序、归并排序这样的复杂排序方法在数据量大的情况下是比选择排序、冒泡排序和插入排序的效率要高的,但是在数据量小的情况下反而要更慢。所以我们可以选定一个阈值,这里选择为 47(和源码中使用的一样)。当需要排序的数据量小于 47 时走插入排序,大于 47 则走快速排序。
private static final int THRESHOLD = 47;
public int[] quickSort(int[] array) {
if (array == null || array.length < 2) {
return array;
}
return quickSort(array, 0, array.length - 1);
}
private int[] quickSort(int[] array, int start, int end) {
// 如果当前需要排序的数据量小于等于THRESHOLD则走插入排序的逻辑,否则继续走快速排序
if (end - start <= THRESHOLD - 1) {
return insertSort(array);
}
// left和right指针分别指向array的第一个和最后一个元素
int left = start, right = end;
/*
取最左边、最右边和最中间的三个元素的中间值作为基准数据,以此来尽量避免每次都取第一个值作为基准数据、
时间复杂度可能退化为O(n^2)的情况出现
*/
int middleOf3Indexs = middleOf3Indexs(array, start, end);
if (middleOf3Indexs != start) {
swap(array, middleOf3Indexs, start);
}
// temp存放的是array中需要比较的基准数据
int temp = array[start];
while (left < right) {
// 首先从right指针开始比较,如果right指针位置处数据大于temp,则将right指针左移
while (left < right && array[right] >= temp) {
right--;
}
// 如果找到一个right指针位置处数据小于temp,则将right指针处数据赋给left指针处
if (left < right) {
array[left++] = array[right];
}
// 然后从left指针开始比较,如果left指针位置处数据小于temp,则将left指针右移
while (left < right && array[left] <= temp) {
left++;
}
// 如果找到一个left指针位置处数据大于temp,则将left指针处数据赋给right指针处
if (left < right) {
array[right--] = array[left];
}
}
// 当left和right指针相等时,此时循环跳出,将之前存放的基准数据赋给当前两个指针共同指向的数据处
array[left] = temp;
// 一次替换后,递归交换基准数据左边的数据
if (start < left - 1) {
array = quickSort(array, start, left - 1);
}
// 之后递归交换基准数据右边的数据
if (right + 1 < end) {
array = quickSort(array, right + 1, end);
}
return array;
}
private int middleOf3Indexs(int[] array, int start, int end) {
int mid = start + ((end - start) >>> 1);
if (array[start] < array[mid]) {
if (array[mid] < array[end]) {
return mid;
} else {
return array[start] < array[end] ? end : start;
}
} else {
if (array[mid] > array[end]) {
return mid;
} else {
return array[start] < array[end] ? start : end;
}
}
}
private void swap(int[] array, int i, int j) {
array[i] = array[i] ^ array[j];
array[j] = array[i] ^ array[j];
array[i] = array[i] ^ array[j];
}5.8 计数排序
以上的七种排序算法都是比较排序,也就是基于元素之间的比较来进行排序的。而下面将要介绍的三种排序算法是非比较排序,首先是计数排序。
计数排序会创建一个临时的数组,里面存放每个数出现的次数。比如一个待排序的数组是[3, 3, 5, 2, 7, 4, 2],那么这个临时数组中记录的数据就是[2, 2, 1, 1, 0, 1]。表示 2 出现了两次、3 出现了两次、4 出现了一次、5 出现了一次、6出现了零次、7 出现了一次。那么最后只需要遍历这个临时数组中的计数值就可以了。
public int[] countingSort(int[] array) {
if (array == null || array.length < 2) {
return array;
}
//记录待排序数组中的最大值
int max = array[0];
//记录待排序数组中的最小值
int min = array[0];
for (int i : array) {
if (i > max) {
max = i;
}
if (i < min) {
min = i;
}
}
int[] temp = new int[max - min + 1];
//记录每个数出现的次数
for (int i : array) {
temp[i - min]++;
}
int index = 0;
for (int i = 0; i < temp.length; i++) {
//当输出一个数之后,当前位置的计数就减一,直到减到0为止
while (temp[i]-- > 0) {
array[index++] = i + min;
}
}
return array;
}
从上面的实现中可以看到,计数排序仅适合数据跨度不大的场景。如果最大值和最小值之间的差距比较大,生成的临时数组就会比较长。比如说一个数组是[2, 1, 3, 1000],最小值是 1,最大值是 1000。那么就会生成一个长度为 1000 的临时数组,但是其中绝大部分的空间都是没有用的,所以这就会导致空间复杂度变得很高。
计数排序是稳定的排序算法,但在上面的实现中并没有体现出这一点,上面的实现没有维护相同元素之间的先后顺序。所以需要做些变换:将临时数组中从第二个元素开始,每个元素都加上前一个元素的值。还是拿之前的[3, 3, 5, 2, 7, 4, 2]数组来举例。计完数后的临时数组为[2, 2, 1, 1, 0, 1],此时做上面的变换,每个数都累加前面的一个数,结果为[2, 4, 5, 6, 6, 7]。这个时候临时数组的含义就不再是每个数出现的次数了,此时记录的是每个数在最后排好序的数组中应该要存放的位置+1(如果有重复的就记录最后一个)。对于上面的待排序数组来说,最后排好序的数组应该为[2, 2, 3, 3, 4, 5, 7]。也就是说,此时各个数最后一次出现的索引位为:1, 3, 4, 5, 6,分别都+1 后就是 2, 4, 5, 6, 7,这不就是上面做过变换之后的数组吗?(没有出现过的数字不管它)所以,此时从后往前遍历原数组中的每一个值,将其减去最小值后,找到其在变换后的临时数组中的索引,也就是找到了最后排好序的数组中的位置了。当然,每次找到临时数组中的索引后,这个位置的数需要-1。这样如果后续有重复的该数字的话,就会插入到当前位置的前一个位置了。由此也说明了遍历必须是从后往前遍历,以此来维护相同数字之间的先后顺序。
public int[] stableCountingSort(int[] array) {
if (array == null || array.length < 2) {
return array;
}
//记录待排序数组中的最大值
int max = array[0];
//记录待排序数组中的最小值
int min = array[0];
for (int i : array) {
if (i > max) {
max = i;
}
if (i < min) {
min = i;
}
}
int[] temp = new int[max - min + 1];
//记录每个数出现的次数
for (int i : array) {
temp[i - min]++;
}
//将temp数组进行转换,记录每个数在最后排好序的数组中应该要存放的位置+1(如果有重复的就记录最后一个)
for (int j = 1; j < temp.length; j++) {
temp[j] += temp[j - 1];
}
int[] sortedArray = new int[array.length];
//这里必须是从后往前遍历,以此来保证稳定性
for (int i = array.length - 1; i >= 0; i--) {
sortedArray[temp[array[i] - min] - 1] = array[i];
temp[array[i] - min]--;
}
return sortedArray;
}5.9 桶排序
上面的计数排序在数组最大值和最小值之间的差值是多少,就会生成一个多大的临时数组,也就是生成了一个这么多的桶,而每个桶中就只插入一个数据。如果差值比较大的话,会比较浪费空间。那么我能不能在一个桶中插入多个数据呢?
当然可以,而这就是桶排序的思路。桶排序类似于哈希表,通过一定的映射规则将数组中的元素映射到不同的桶中,每个桶内进行内部排序,最后将每个桶按顺序输出就行了。桶排序执行的高效与否和是否是稳定的取决于哈希散列的算法以及内部排序的结果。需要注意的是,这个映射算法并不是常规的映射算法,要求是每个桶中的所有数都要比前一个桶中的所有数都要大,这样最后输出的才是一个排好序的结果。比如说第一个桶中存 1-30 的数字,第二个桶中存 31-60 的数字,第三个桶中存 61-90 的数字...以此类推。下面给出一种实现:
public int[] bucketSort(int[] array) {
if (array == null || array.length < 2) {
return array;
}
//记录待排序数组中的最大值
int max = array[0];
//记录待排序数组中的最小值
int min = array[0];
for (int i : array) {
if (i > max) {
max = i;
}
if (i < min) {
min = i;
}
}
//计算桶的数量(可以自定义实现)
int bucketNumber = (max - min) / array.length + 1;
List<Integer>[] buckets = new ArrayList[bucketNumber];
//计算每个桶存数的范围(可以自定义实现或者不用实现)
int bucketRange = (max - min + 1) / bucketNumber;
for (int value : array) {
//计算应该放到哪个桶中(可以自定义实现)
int bucketIndex = (value - min) / (bucketRange + 1);
//延迟初始化
if (buckets[bucketIndex] == null) {
buckets[bucketIndex] = new ArrayList<>();
}
//放入指定的桶
buckets[bucketIndex].add(value);
}
int index = 0;
for (List<Integer> bucket : buckets) {
//对每个桶进行内部排序,我这里使用的是快速排序,也可以使用别的排序算法,当然也可以继续递归去做桶排序
quickSort(bucket);
if (bucket == null) {
continue;
}
//将不为null的桶中的数据按顺序写回到array数组中
for (Integer integer : bucket) {
array[index++] = integer;
}
}
return array;
}5.10 基数排序
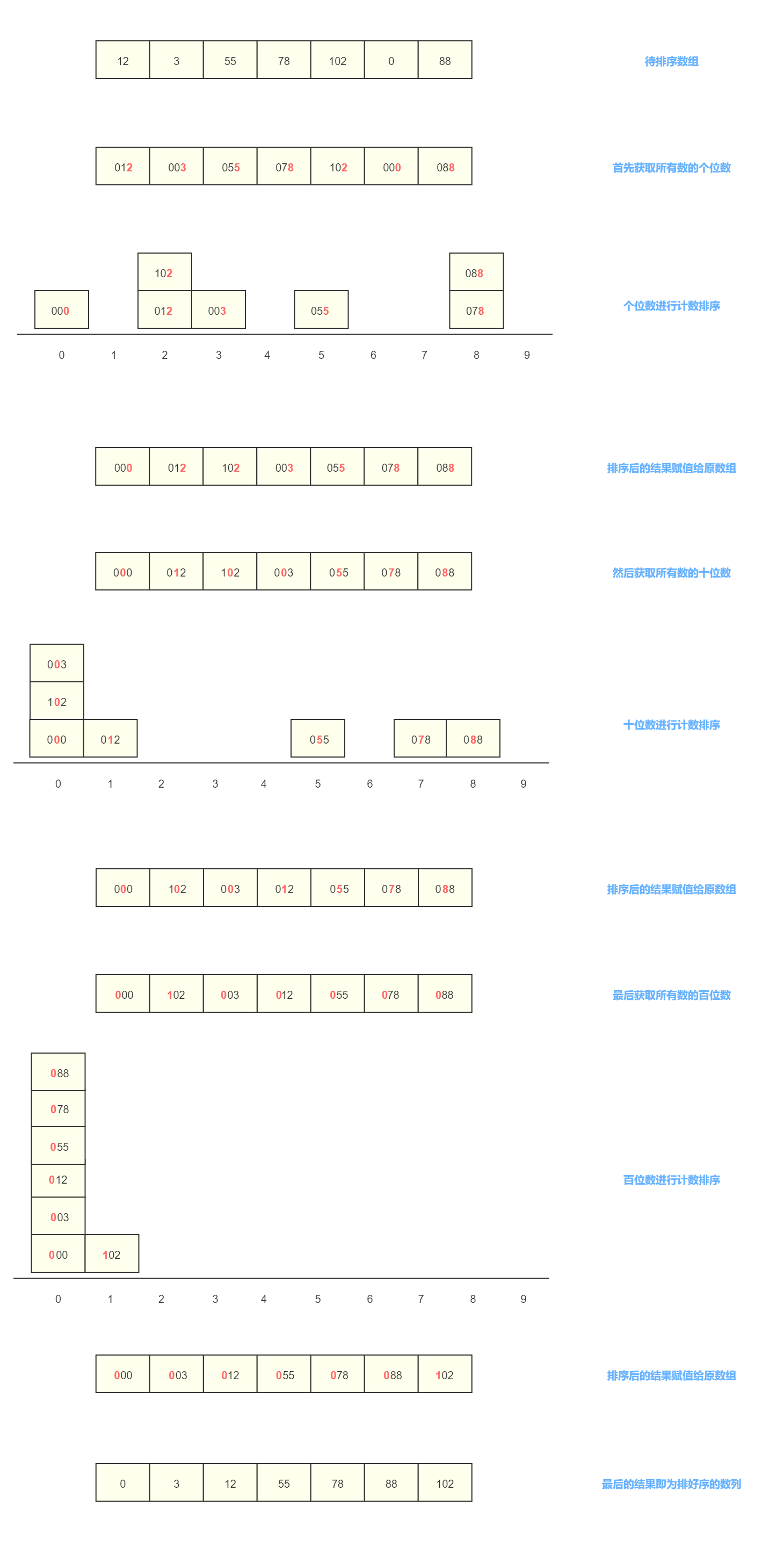
基数排序不是根据一个数的整体来进行排序的,而是将数的每一位上的数字进行排序。比如说第一轮排序,我拿到待排序数组中所有数个位上的数字来进行排序;第二轮排序我拿到待排序数组中所有数十位上的数字来进行排序;第三轮排序我拿到待排序数组中所有数百位上的数字来进行排序...以此类推。每一轮的排序都会累加上一轮所有前几位上排序的结果,最终的结果就会是一个有序的数列。基数排序一般是对所有非负整数进行排序的,但是也可以有别的手段来去掉这种限制(比如都加一个固定的数或者都乘一个固定的数,排完序后再恢复等等)。基数排序和桶排序很像,桶排序是按数值的区间进行划分,而基数排序是按数的位数进行划分。同时这两个排序都是需要依靠其他排序算法来实现的(如果不递归调用桶排序本身的话)。基数排序每一轮的内部排序会使用到计数排序来实现,因为每一位上的数字无非就是 0-9,是一个小范围的数,所以使用计数排序很合适。
基数排序执行示意图:
public int[] radixSort(int[] array) {
if (array == null || array.length < 2) {
return array;
}
//记录待排序数组中的最大值
int max = array[0];
for (int i : array) {
if (i > max) {
max = i;
}
}
//获取最大值的位数
int maxDigits = 0;
while (max != 0) {
max /= 10;
maxDigits++;
}
//用来计数排序的临时数组
int[] temp = new int[10];
//用来存放每轮排序后的结果
int[] sortedArray = new int[array.length];
for (int d = 1; d <= maxDigits; d++) {
//每次循环开始前都要清空temp数组中的值
replaceArray(temp, null);
//记录每个数出现的次数
for (int a : array) {
temp[getNumberFromDigit(a, d)]++;
}
//将temp数组进行转换,记录每个数在最后排好序的数组中应该要存放的位置+1(如果有重复的就记录最后一个)
for (int j = 1; j < temp.length; j++) {
temp[j] += temp[j - 1];
}
//这里必须是从后往前遍历,以此来保证稳定性
for (int i = array.length - 1; i >= 0; i--) {
int index = getNumberFromDigit(array[i], d);
sortedArray[temp[index] - 1] = array[i];
temp[index]--;
}
//一轮计数排序过后,将这次排好序的结果赋值给原数组
replaceArray(array, sortedArray);
}
return array;
}
private final static int[] sizeTable = {1, 10, 100, 1000, 10000, 100000, 1000000, 10000000, 100000000, 1000000000};
/**
* 获取指定位数上的数字是多少
*/
private int getNumberFromDigit(int number, int digit) {
if (digit < 0) {
return -1;
}
return (number / sizeTable[digit - 1]) % 10;
}
private void replaceArray(int[] originalArray, int[] replaceArray) {
if (replaceArray == null) {
for (int i = 0; i < originalArray.length; i++) {
originalArray[i] = 0;
}
} else {
for (int i = 0; i < originalArray.length; i++) {
originalArray[i] = replaceArray[i];
}
}
}5.11 复杂度及稳定性
<table style="text-align: center;">
<tr>
<td rowspan="2">排序算法</td>
<td colspan="3">时间复杂度</td>
<td rowspan="2">空间复杂度</td>
<td rowspan="2">稳定性</td>
</tr>
<tr>
<td>平均情况</td>
<td>最好情况</td>
<td>最坏情况</td>
</tr>
<tr>
<td>冒泡排序</td>
<td>O(n<sup>2</sup>)</td>
<td>O(n)</td>
<td>O(n<sup>2</sup>)</td>
<td>O(1)</td>
<td>稳定</td>
</tr>
<tr>
<td>选择排序</td>
<td>O(n<sup>2</sup>)</td>
<td>O(n<sup>2</sup>)</td>
<td>O(n<sup>2</sup>)</td>
<td>O(1)</td>
<td>不稳定</td>
</tr>
<tr>
<td>插入排序</td>
<td>O(n<sup>2</sup>)</td>
<td>O(n)</td>
<td>O(n<sup>2</sup>)</td>
<td>O(1)</td>
<td>稳定</td>
</tr>
<tr>
<td>希尔排序</td>
<td colspan="3">取决于增量的选择</td>
<td>O(1)</td>
<td>不稳定</td>
</tr>
<tr>
<td>堆排序</td>
<td>O(nlog<sub>2</sub>n)</td>
<td>O(nlog<sub>2</sub>n)</td>
<td>O(nlog<sub>2</sub>n)</td>
<td>O(1)</td>
<td>不稳定</td>
</tr>
<tr>
<td>归并排序</td>
<td>O(nlog<sub>2</sub>n)</td>
<td>O(nlog<sub>2</sub>n)</td>
<td>O(nlog<sub>2</sub>n)</td>
<td>O(n)</td>
<td>稳定</td>
</tr>
<tr>
<td>快速排序</td>
<td>O(nlog<sub>2</sub>n)</td>
<td>O(nlog<sub>2</sub>n)</td>
<td>O(n<sup>2</sup>)</td>
<td>O(nlog<sub>2</sub>n)</td>
<td>不稳定</td>
</tr>
<tr>
<td>计数排序</td>
<td>O(n+k)</td>
<td>O(n+k)</td>
<td>O(n+k)</td>
<td>O(k)</td>
<td>稳定</td>
</tr>
<tr>
<td>桶排序</td>
<td colspan="3">取决于桶散列的结果和内部排序算法的时间复杂度</td>
<td>O(n+l)</td>
<td>稳定</td>
</tr>
<tr>
<td>基数排序</td>
<td>O(d*(n+r))</td>
<td>O(d*(n+r))</td>
<td>O(d*(n+r))</td>
<td>O(n+r)</td>
<td>稳定</td>
</tr>
</table>
> 其中:
>
> k 表示计数排序中最大值和最小值之间的差值;
>
> l 表示桶排序中桶的个数;
>
> d 表示基数排序中最大值的位数,r 表示是多少进制;
>
> 希尔排序的时间复杂度很大程度上取决于增量 gap sequence 的选择,不同的增量会有不同的时间复杂度。文中使用的 “gap=length/2” 和 “gap=gap/2” 是一种常用的方式,也被称为希尔增量,但其并不是最优的。
六、双指针
算法中双指针主要包括首尾双指针(对撞双指针),快慢双指针;通过指针的移动解决问题。
数组或字符串相关的问题经常需要运用双指针来求解。而双指针又分为快慢指针和左右指针。
其中快慢指针主要用于解决链表问题,而首尾指针用于解决数组问题。
6.1 快慢双指针
顾名思义,快慢指针是指一个指针走的快,一个指针走得慢。
1. 链表中倒数第 k 个节点
链表中,通过快慢双指针求链表中倒数第 k 个节点。
题目:输入一个链表,输出该链表中倒数第 k 个节点。
解题思路:快慢指针,先让快指针走 k 步,然后两个指针同时走,当快指针到头时,慢指针就是链表倒数第 k 个节点。
使用双指针可以不用统计链表长度。
- 初始化:前指针,后指针,双指针都指向头节点 head。
- 构建双指针距离:前指针先向前走 k 步。
- 双指针同时移动:循环,直到前指针到尾节点跳出,后指针指向倒数第 k 个节点。
- 返回值:返回后指针即可。
- 算法代码:
class Solution {
public ListNode getKthFromEnd(ListNode head, int k) {
if(head==null||k<=0)
{
return null;
}
//定义两个指针节点
ListNode pre=head;
ListNode last=head;
//先将一个节点往后移动k-1个距离
while(pre!=null && k>0){
pre=pre.next;
k--;
}
//一起移动,第一个节点移动到末尾,第二个结点移动到倒数第k个节点
while(pre!=null)
{
pre=pre.next;
last=last.next;
}
return last;
}
}2. 判断链表是否有环
思路:快指针每次走两步,慢指针每次走一步。如果链表中存在环,总有那么一个时刻快指针比慢指针多走了一圈,此时他们相遇。
boolean hasCycle(ListNode head){
ListNode fast, slow;
fast = slow = head;
while(fast != null && fast.next != null){
fast = fast.next.next;
slow = slow.next;
if(slow == fast){
return true;
}
}
return false;
}6.2 首尾双指针
又称对撞双指针,左右双指针。指双指针中一个指针在数组的最左侧,而另一个在最右侧。通过判断,可以分别让两侧的指针向中间移动,以求解问题。
1. 和为 s 的两个数字
题目:输入一个递增排序的数组和一个数字 s,在数组中查找两个数,使得它们的和正好是 s。如果有多对数字的和等于 s,则输出任意一对即可。解题思路:首尾双指针,判断两数的和与 target 进行比较,往中间移动。
算法代码:
class Solution {
public int[] twoSum(int[] nums, int target) {
int i=0, j=nums.length-1;
while(i<j){
int s=nums[i]+nums[j];
if(s<target) i++;
else if(s>target) j--;
else return new int[] {nums[i], nums[j]};
}
return new int[0];
}
}
2. 调整数组顺序使奇数位于偶数前面
题目:输入一个整数数组,实现一个函数来调整该数组中数字的顺序,使得所有奇数位于数组的前半部分,所有偶数位于数组的后半部分。
解题思路:首尾双指针,left 右移直到指偶数,right 左移直到指奇数,交换。
算法代码:
class Solution {
public int[] exchange(int[] nums) {
int left=0,right=nums.length-1;
int tmp;
while(left<right){
if(nums[left]%2==1) left++;
else if(nums[right]%2==0) right--;
else{
tmp=nums[left];
nums[left]=nums[right];
nums[right]=tmp;
left++;
right--;
}
}
return nums;
}
}七、栈
栈的英文为(stack)。
栈是一个先入后出(FILO-First In Last Out)的有序列表。
栈(stack)是限制线性表中元素的插入和删除只能在线性表的同一端进行的一种特殊线性表。允许插入和删除的一端,为变化的一端,称为栈顶(Top),另一端为固定的一端,称为栈底(Bottom)。
根据栈的定义可知,最先放入栈中元素在栈底,最后放入的元素在栈顶,而删除元素刚好相反,最后放入的元素最先删除,最先放入的元素最后删除。
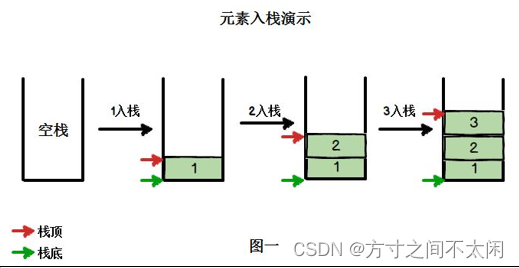
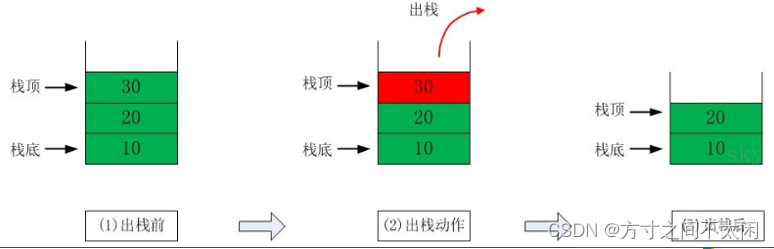
那么栈主要的操作就是入栈和出栈了。
关于栈的应用场景,其实还是有很多的:
子程序的调用:在跳往子程序前,会先将下个指令的地址存到堆栈中,直到子程序执行完后再将地址取出,以回到原来的程序中。
处理递归调用:和子程序的调用类似,只是除了储存下一个指令的地址外,也将参数、区域变量等数据存入堆栈中。
表达式的转换[中缀表达式转后缀表达式]与求值(实际解决)。
二叉树的遍历。
图形的深度优先(depth 一 first)搜索法。
八、队列
数据结构中程序基本可以分为两大类:线性结构和非线性结构;
- 线性结构代表:数组、队列、链表和栈;
- 非线性结构代表:多维数组(包括二维,但是归到这里有些牵强)、树、图、广义表;
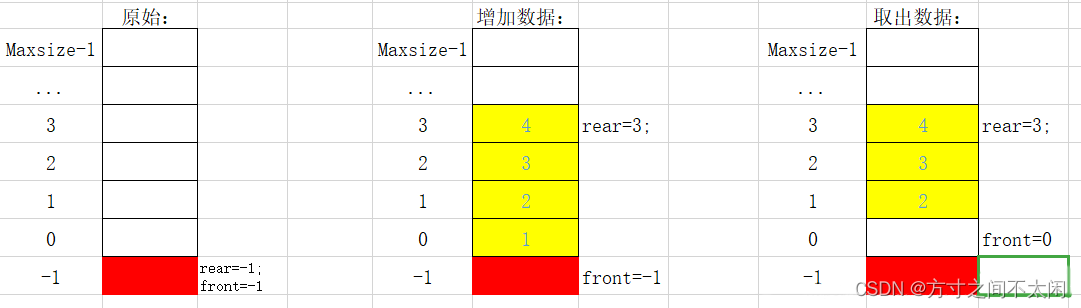
队列的特点是先进先出,这个很重要;举一个很恰当的例子,在实际生活中,银行的 “叫号系统”便是队列很好的诠释者 —— —— 按照到银行的顺序依次排号,先来人的优先服务 (出队)有了思路以后事情便开始简单,在进入实际代码前,不妨先将思路整理为一个简单的图(先默认利用数组实现):
- MaxSize 为数组的长度,MaxSize-1 为最大可存储的单元;
- front 为队列的头元素所在的前一个位置,rear 表示尾元素所在的当前位置;
- 当 front == rear 表示队空;当 MaxSize-1 == rear 为队满;
import java.util.Scanner;
public class Queue {
public static void main(String[] args){
ArrayQueue arrayQueue=new ArrayQueue(5);//4.方便测试所以没有定义太大
char key=' ';//5.键盘交互,接收用户输入
Scanner scanner=new Scanner(System.in);
boolean loop=true;
while(loop){
System.out.println("s(show):显示队列");
System.out.println("e(exit):退出程序");
System.out.println("a(add):向队列添加元素");
System.out.println("g(get):向队列取出元素");
System.out.println("h(head):查看队列的头数据");
key=scanner.next().charAt(0);
if (key<97) key+=32; //实现大小写都可判断
switch (key){
case 's' :
arrayQueue.showQueue();
break;
case 'a':
System.out.println("请输入一个数字");
arrayQueue.addQueue(scanner.nextInt());
break;
case 'g' :
try {
System.out.println("您取到的数据为:"+ arrayQueue.getQueue());
} catch (Exception e){
System.out.println(e.getMessage());
}break;
case 'h' :
try {
System.out.println("当前的头数据为:"+ arrayQueue.headQueue());
} catch (Exception e){
System.out.println(e.getMessage());
}break;
case 'e' :
scanner.close();//关闭输入
loop=false;
break;
}
}
System.out.println("**********程序已退出*********");
}
}
class ArrayQueue{//1.创建一个实现队列的类
private int MaxSize; //队列的最大存储容量
private int [] array; //要存储队列的数组
private int front; //取出时移动的指针,指向队列前的一个位置;
private int rear; //存储时移动的指针,指向队列当前存储到的位置(最后一个数据);
//创建队列
public ArrayQueue(int arrMaxSize){//2.设置构造器
MaxSize=arrMaxSize;
rear=-1;front=-1;
array=new int[MaxSize];
}
//判断队列是否空
public boolean isEmpty(){//3.一些必要的方法
return rear==front;
}
//判断队列是否满
public boolean isFull(){
return rear==MaxSize-1;
}
//添加数据
public void addQueue(int q){
if(isFull()) System.out.println("队列已满,不可添加数据!");
else {
array[++rear]=q;//java可以这么写
System.out.println("添加数据成功");
}
}
//取出数据
public int getQueue(){
if (!isEmpty()){
return array[++front];
}
throw new RuntimeException("队列为空");//没有合适的返回值,用异常
}
//显示当前队列所有数据
public void showQueue(){
if (isEmpty()) {
System.out.println("队列为空,无可打印数据");
return;
}
for (int i=0;i<array.length;i++){
System.out.printf("%d ",array[i]);
}
System.out.println();
}
//返回当前队列的头数据
public int headQueue(){
if (isEmpty()) throw new NumberFormatException("队列为空,无头数据");
return array[front+1];
}
}