代码随想录第二十六天 | 回溯算法P3 |● 39. ● 40.● 131.

39. 组合总和

给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ，找出 candidates 中可以使数字和为目标数 target 的所有 不同组合 ，并以列表形式返回。你可以按 任意顺序 返回这些组合。

candidates 中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同，则两种组合是不同的。

对于给定的输入，保证和为 target 的不同组合数少于 150 个。

示例 1：

输入：candidates = [2,3,6,7], target = 7
输出：[[2,2,3],[7]]
解释：
2 和 3 可以形成一组候选，2 + 2 + 3 = 7 。注意 2 可以使用多次。
7 也是一个候选， 7 = 7 。
仅有这两种组合。

示例 2：

输入: candidates = [2,3,5], target = 8
输出: [[2,2,2,2],[2,3,3],[3,5]]

示例 3：

输入: candidates = [2], target = 1
输出: []

思路

与组合类似的做法，回溯三步曲：

回溯函数参数及返回值：candidate、target 以及 start(记录当前遍历起始位置)

终止条件:当path和为target 则停止

单层遍历的操作：依然是for循环横向遍历回溯纵向遍历， for循环里 i 从start 开始

未剪枝代码如下

class Solution {
    public List<List<Integer>> resList = new ArrayList<List<Integer>>();
    public LinkedList<Integer> path = new LinkedList<>();
    public List<List<Integer>> combinationSum(int[] candidates, int target) {
        backtracking(candidates, target, 0);
        return resList;
    }
    public void backtracking(int [] candidates, int target, int start){
        if(getSum(path) == target){
            resList.add(new ArrayList<>(path));
            return;
        }
        if(getSum(path) > target){
            return;
        }

        for(int i = start; i < candidates.length; i++){
            path.addLast(candidates[i]);
            backtracking(candidates, target, i);
            path.removeLast();
        }
    }
    public int getSum(List<Integer> path){
        int sum = 0;
        for(int i  : path){
            sum += i;
        }
        return sum;
    }
}

剪枝

在每层遍历的过程中，如果当前加入的数会使得 path和大于 target 那么就不需要继续遍历，但仍然存在一个问题，那就是这需要candidates是升序的，因为只有升序才能保证后续数均会使得sum大于 target。

代码如下

class Solution {
    public List<List<Integer>> resList = new ArrayList<List<Integer>>();
    public LinkedList<Integer> path = new LinkedList<>();
    public List<List<Integer>> combinationSum(int[] candidates, int target) {
        Arrays.sort(candidates);
        backtracking(candidates, target, 0);
        return resList;
    }
    public void backtracking(int [] candidates, int target, int start){
        if(getSum(path) == target){
            resList.add(new ArrayList<>(path));
            return;
        }
        if(getSum(path) > target){
            return;
        }

        for(int i = start; i < candidates.length && getSum(path) + candidates[i] <= target; i++){
            path.addLast(candidates[i]);
            backtracking(candidates, target, i);
            path.removeLast();
        }
    }
    public int getSum(List<Integer> path){
        int sum = 0;
        for(int i  : path){
            sum += i;
        }
        return sum;
    }
}

什么时候需要startIndex

本题还需要startIndex来控制for循环的起始位置，对于组合问题，什么时候需要startIndex呢？

我举过例子，如果是一个集合来求组合的话，就需要startIndex，例如：77.组合 (opens new window)，216.组合总和III (opens new window)。

如果是多个集合取组合，各个集合之间相互不影响，那么就不用startIndex，例如：17.电话号码的字母组合(opens new window)

注意以上只是说求组合的情况，如果是排列问题，又是另一套分析的套路，后面我在讲解排列的时候会重点介绍。

40.组合总和II

给定一个候选人编号的集合 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

candidates 中的每个数字在每个组合中只能使用一次。

注意：解集不能包含重复的组合。

示例 1:

输入: candidates = [10,1,2,7,6,1,5], target = 8,
输出:
[
[1,1,6],
[1,2,5],
[1,7],
[2,6]
]

示例 2:

输入: candidates = [2,5,2,1,2], target = 5,
输出:
[
[1,2,2],
[5]
]

思路

这个与上面的区别在于

1、数不能重复使用，那么只需要更改递归调用回溯函数中的参数 start即可

2、集合（数组candidates）有重复元素，但还不能有重复的组合。

对于2 求出结果后用set/map去重，会超时

所以需要在回溯的过程中进行去重。

这里考虑什么时候会出现重复组合，

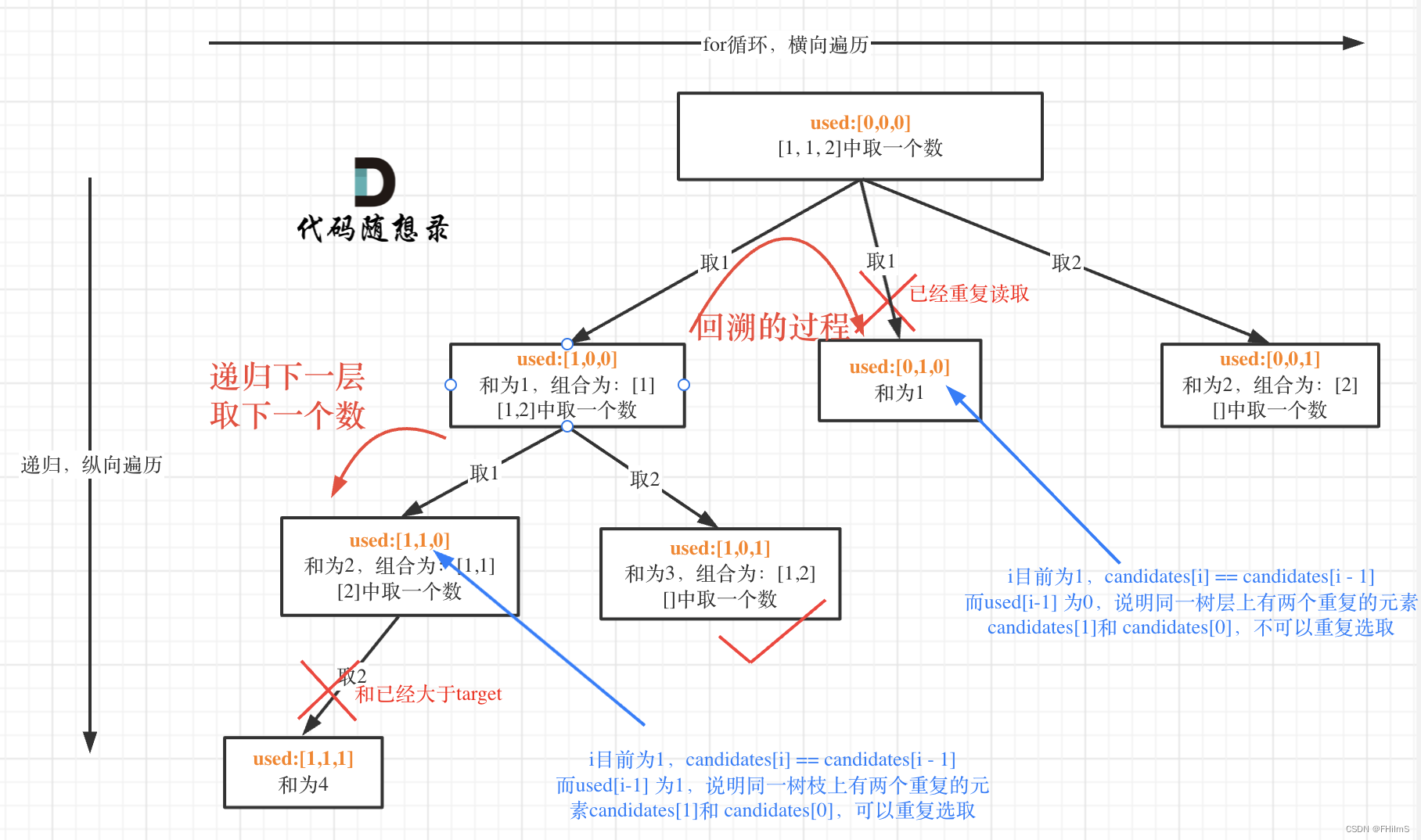
组合问题可以抽象为树形结构，那么“使用过”在这个树形结构上是有两个维度的，一个维度是同一树枝上使用过，一个维度是同一树层上使用过。没有理解这两个层面上的“使用过” 是造成大家没有彻底理解去重的根本原因。

那么问题来了，我们是要同一树层上使用过，还是同一树枝上使用过呢？

回看一下题目，元素在同一个组合内是可以重复的，怎么重复都没事，但两个组合不能相同。

所以我们要去重的是同一树层上的“使用过”，同一树枝上的都是一个组合里的元素，不用去重。

而数层去重，需要对数组进行排序。

要去重的是“同一树层上的使用过”，如何判断同一树层上元素（相同的元素）是否使用过了呢。

如果candidates[i] == candidates[i - 1] 并且 used[i - 1] == false，就说明：前一个树枝，使用了candidates[i - 1]，也就是说同一树层使用过candidates[i - 1]。

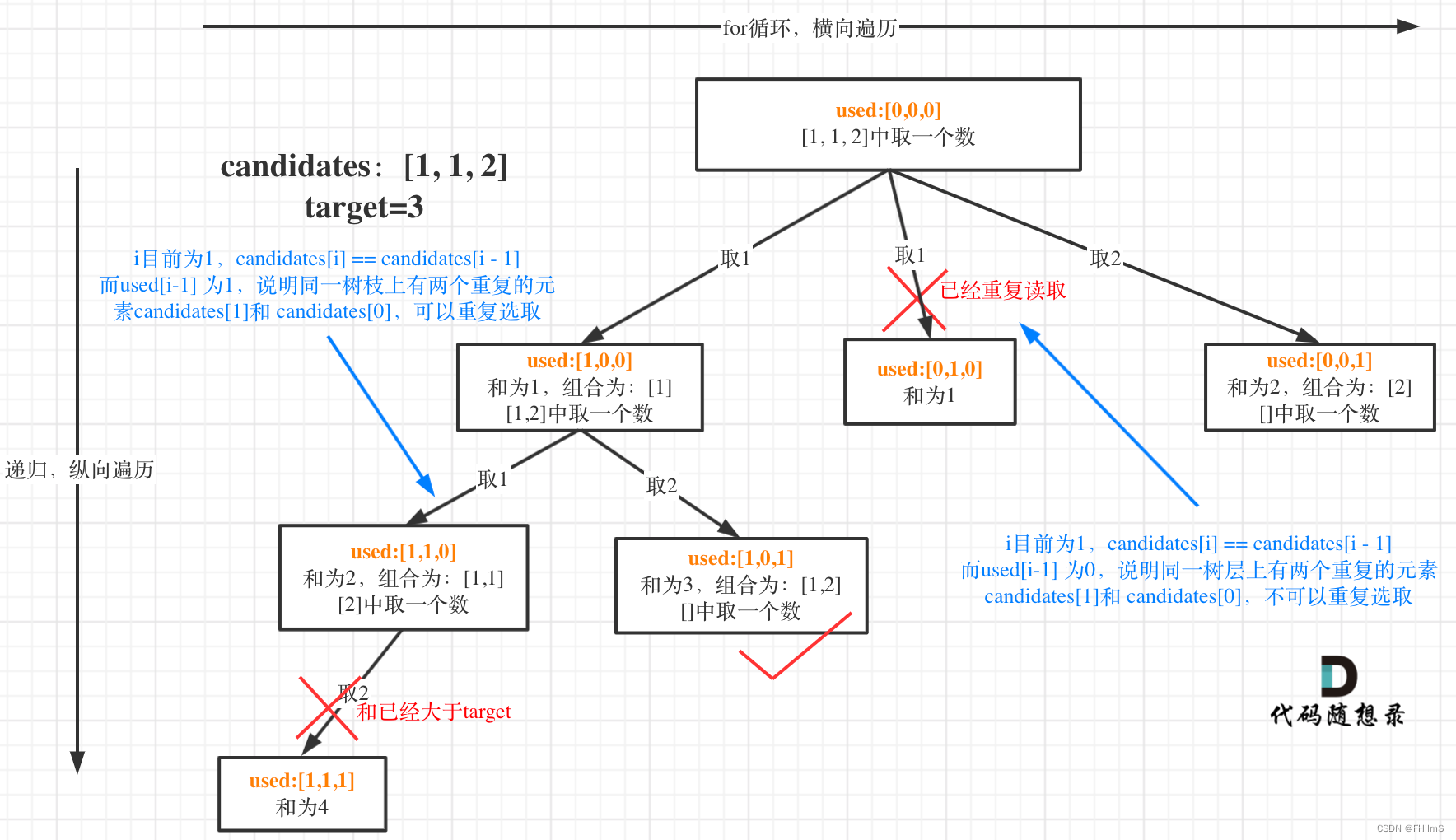
在图中将used的变化用橘黄色标注上，可以看出在candidates[i] == candidates[i - 1]相同的情况下：

used[i - 1] == true，说明同一树枝candidates[i - 1]使用过
used[i - 1] == false，说明同一树层candidates[i - 1]使用过

可能有的录友想，为什么 used[i - 1] == false 就是同一树层呢，因为同一树层，used[i - 1] == false 才能表示，当前取的 candidates[i] 是从 candidates[i - 1] 回溯而来的。

而 used[i - 1] == true，说明是进入下一层递归，去下一个数，所以是树枝上，如图所示：

剪枝 + 去重

利用used数组去重：

class Solution {
    public List<List<Integer>> resList = new ArrayList<List<Integer>>();
    public LinkedList<Integer> path = new LinkedList<>();
    public boolean [] used;
    public List<List<Integer>> combinationSum2(int[] candidates, int target) {
        Arrays.sort(candidates);
        used = new boolean[candidates.length];
        Arrays.fill(used, false);
        backtracking(candidates, target, 0, used);
        return resList;
    }
    public void backtracking(int [] candidates, int target, int start, boolean[] used){
        if(getSum(path) == target){
            resList.add(new ArrayList<>(path));
            return;
        }
        if(getSum(path) > target){
            return;
        }
        //<= target 剪枝
        for(int i = start; i < candidates.length && getSum(path) + candidates[i] <= target; i++){
            // 利用used数组去重 
            if(i > 0 && candidates[i] == candidates[i-1] && !used[i-1]){
                continue;
            }
            path.addLast(candidates[i]);
            used[i] = true;
            backtracking(candidates, target, i + 1, used);
            used[i] = false;
            path.removeLast();
        }
    }
    public int getSum(List<Integer> path){
        int sum = 0;
        for(int i  : path){
            sum += i;
        }
        return sum;
    }
}

直接利用start去重：

这里考虑当出现同一树层重复时，除了满足candidate[i] == candidate[i-1]外，还要知道，此时 i 大于当前的start。这是因为对每层，start固定，随层深入start递增，每层 i 从 start开始，从左往右递增。而对同一树枝重复，当出现candidate[i] == candidate[i-1]时，此时的 i 一定等于start(candidate升序) 所以可利用这一点实现同一树层重复去重。

代码如下

class Solution {
    public List<List<Integer>> resList = new ArrayList<List<Integer>>();
    public LinkedList<Integer> path = new LinkedList<>();
    public List<List<Integer>> combinationSum2(int[] candidates, int target) {
        Arrays.sort(candidates);
        backtracking(candidates, target, 0);
        return resList;
    }
    public void backtracking(int [] candidates, int target, int start){
        if(getSum(path) == target){
            resList.add(new ArrayList<>(path));
            return;
        }
        if(getSum(path) > target){
            return;
        }
        //<= target 剪枝
        for(int i = start; i < candidates.length && getSum(path) + candidates[i] <= target; i++){
            // 利用start去重
            if(i > start && candidates[i] == candidates[i-1]){
                //此时为 同一树层重复
                continue;
            }
            path.addLast(candidates[i]);
            backtracking(candidates, target, i + 1);
            path.removeLast();
        }
    }
    public int getSum(List<Integer> path){
        int sum = 0;
        for(int i  : path){
            sum += i;
        }
        return sum;
    }
}

总结

本题同样是求组合总和，但就是因为其数组candidates有重复元素，而要求不能有重复的组合，所以相对于39.组合总和 (opens new window)难度提升了不少。

注意对数层重复与树枝重复的理解

131.分割回文串

给你一个字符串 s，请你将 s 分割成一些子串，使每个子串都是 回文串 。返回 s 所有可能的分割方案。

示例 1：

输入：s = "aab"
输出：[["a","a","b"],["aa","b"]]

示例 2：

输入：s = "a"
输出：[["a"]]

提示：

1 <= s.length <= 16
s 仅由小写英文字母组成

思路

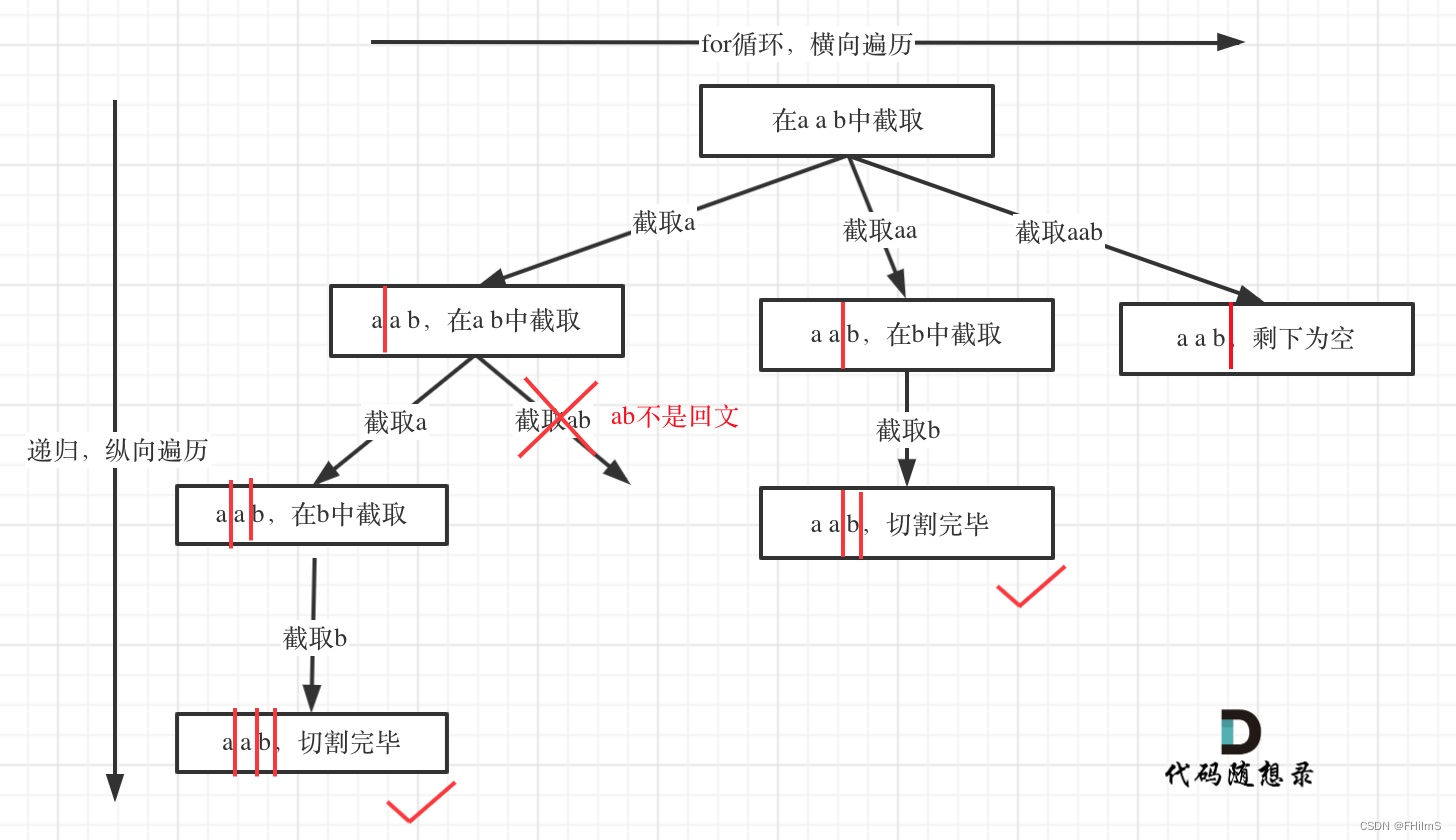
本体存在如下几个难点：

切割问题可以抽象为组合问题
如何模拟那些切割线
切割问题中递归如何终止
在递归循环中如何截取子串
如何判断回文

注：[ startIndex， i ] 即为切割的子串。

代码

根据组合问题的代码模板，三步曲

class Solution {
    public List<List<String>> resList = new ArrayList<>();
    public LinkedList<String> path = new LinkedList<String>();
    public List<List<String>> partition(String s) {
        if(s == null || s.length() == 0) return resList;
        backtracking(s, 0);
        return resList;
    }
    public void backtracking(String s, int startIndex){
        if(startIndex >= s.length()){
            resList.add(new ArrayList<String>(path));
            return;
        }
        for(int i = startIndex; i < s.length(); i++){
            if(isPrime(s, startIndex, i)){
                //注意substring 不包含end
                path.addLast(s.substring(startIndex, i + 1));
                backtracking(s, i+1);
                path.removeLast();
            }
        }
    }
    public boolean isPrime(String s, int startIndex, int i){
        while(startIndex <= i){
            if(s.charAt(startIndex) != s.charAt(i)){
                return false;
            }
            startIndex++;
            i--;
        }
        return true;
    }
}