一.题目描述
小美拿到了一个排列,其中初始所有元素都是红色,但有些元素被染成了白色。
小美每次操作可以选择交换任意两个红色元素的位置。她希望操作尽可能少的次数使得数组变成非降序,你能帮帮她吗?
排列是指:一个长度为n的数组,其中1到n每个元素恰好出现了一次。
输入描述
第一行输入一个正整数n,代表数组的长度.
第二行输入几个正整数ai,代表数组的元素。
第三行输入一个长度为n的字符串,代表数组元素的染色情况。第i个字符为'R"代表第i个元素被染成红色,为"W"代表初始的白色.
1 ≤n≤ 10^5
1<=ai<=n
输出描述
如果无法完成排序,请输出 -1.
否则输出一个整数,代表操作的最小次数。
示例 1
输入
4
1 3 2 4
WRRW
输出
1
说明
第一次操作,交换 2和 3,数组变成[1,2,3,4]
二.分析
- 题目中写了:排列是指:一个长度为n的数组,其中1到n每个元素恰好出现了一次。也就意味着上面操作使得非降序,是指升序,不存在两个数字一样的情况
- 每次操作可以选择交换任意两个红色元素的位置,什么意思?意味着不可以动白色的染色体
- 需要思考什么情况下不可以完成排序:当这个位置是排序好的,比如1,2,3,4,5,而他的排序是2,1,3,4,5,我们可以看到2,1是未排序好的,当他的下标+1不是他的数据,并且它是白色染色体不可以挪动,那么是必定无法排序成功的。此时返回-1
- 最小操作次数:1,2,4,3,5,每次都让一个数字回到它本来的位置,挪动的次数就是最少
/* 测试1
4
1 3 2 4
WRRW
1
*/
int main()
{
int n;
cin >> n; //录入第一行
int* arr = new int[n];//录入第二行
char* brr = new char[n]; //录入第三行
for (int i = 0; i < n; i++)
cin >> arr[i];
for (int i = 0; i < n; i++)
cin >> brr[i];
for (int i = 0; i < n; i++)//排除不可能的情况
{
if(arr[i]!=i+1 && brr[i] == 'W')//'W'不能移动
{
cout << -1;
delete []arr;
delete[]brr;
return 0;
}//位置错了 if 删了 提交
}
//1 3 2 4
//1 2 3 4 ,怎么次数最少? 可能是每次能处理一个正确的数字
//4 3 2 1
int count = 0;//计数器
int tmp;
for (int i = 0; i < n; i++)
{
while (arr[i] != i + 1)//不是正确的位置,交换
{
//把当前位置和它应该放的位置交换
tmp = arr[arr[i] - 1];
arr[arr[i] - 1] = arr[i];
arr[i] = tmp;
count++;
}
}
cout << count;
delete []arr;
delete[]brr;
return 0;
}注意点演示:

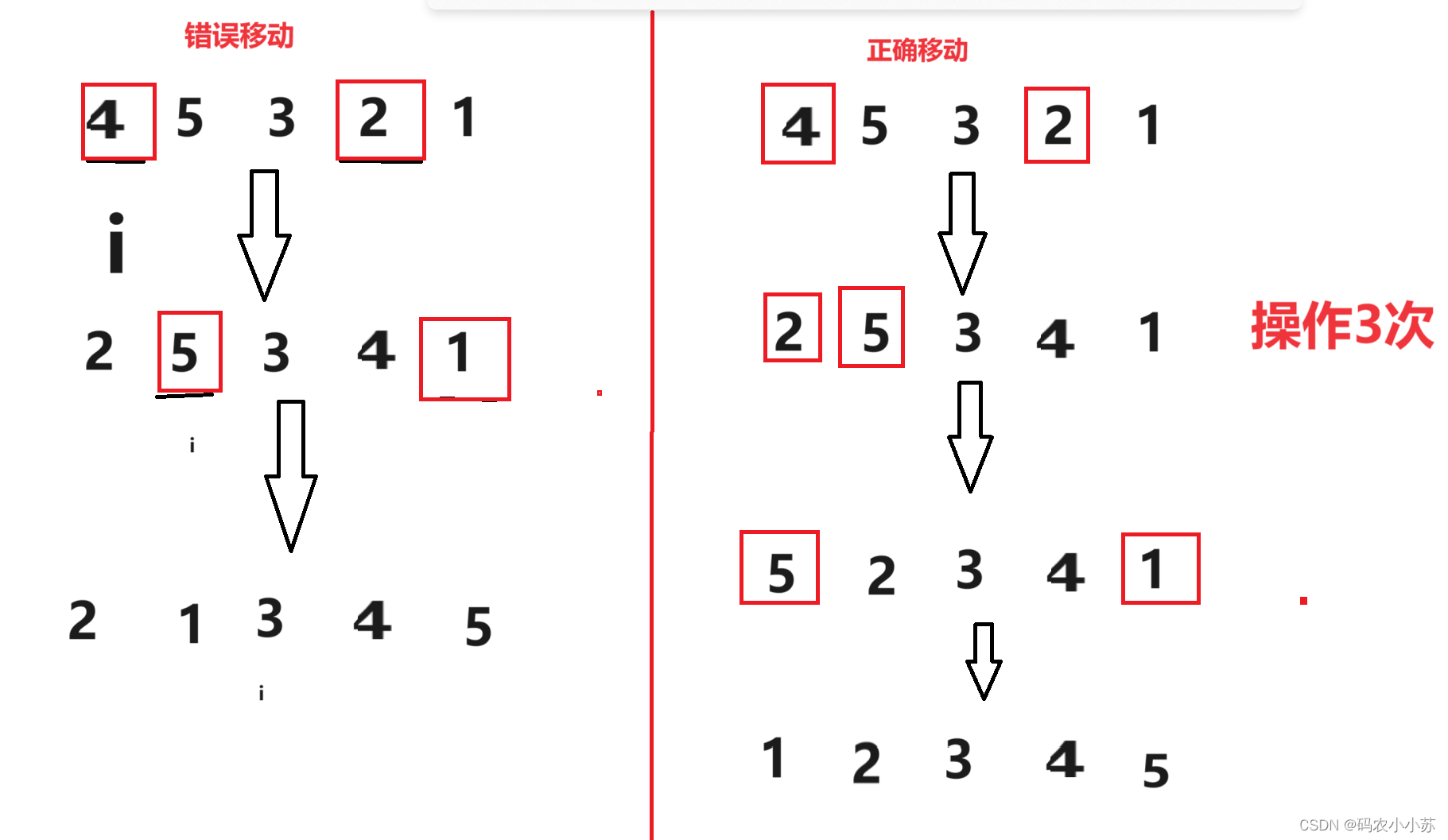
一定要区分两种不同的移动方式:

如果只是简单地遍历一遍是不可以达到排序的效果,必须一直挪动,直到当前位置是想要的数字为之,否则不可以。
下面演示第一种和第二种移动方式的区别:(错误演示)
本篇完!