Part.I Introduction
本文主要记录一下笔者使用 GSL 过程当中所做的一些笔记。

Chap.I 传送门
一些传送门
- GSL源码(CMakeList 版本-Windows)
- GSL源码(configure 版本-Linux)
- GSL 在线文档
- GSL 文档下载
Chap.II GSL 简介
GSL 全称 GNU Scientific Library,即 GNU 科学计算库。GNU 是什么东西呢?GNU 是一个自由的操作系统,其内容软件完全以 GPL 方式发布。GPL 又是什么东西?不要急~要想理解GNU 操作系统,必须先了解 GUN Project ,GNU计划、GNU项目,随你怎么翻译好了…… 它又被译为 革奴计划 ,是一个自由软件集体协作计划,1983年9月27日由理查德·斯托曼在麻省理工学院公开发起。它的目的是创建一套完全自由的操作系统,称为GNU1。GNU 全称 GNU’s Not Unix!,递归定义缩写。
GPL 的全称是 GNU General Public License ,被翻译为 GNU通用公共许可协议 ,缩写为 GPL 或 GNU GPL ,说到底,这只不过是一个协议系列,那这一系列协议有啥特点呢?它有两个特点(copyleft):
- 一方面,它给予了用户充分的自由,允许用户 运行、学习、共享和修改软件 ;
- 而另一方面,它死死限制了用户的一个方面的自由,那就是:GPL的派生作品只能以相同的许可证 发布 。这两个特点结合起来翻译成人话就是“软件随便用,源码也给你,随你怎么copy怎么修改,这都是你的自由,但是!你不能将大家伙的劳动成果变成你一个人私有的!”
就简单将 GNU 理解为一个项目,在这个项目中需要遵守 GPL 协议,即可以运行、学习、共享和修改 GNU 项目中的软件,但是不能据为己有。而 GSL 就是 GNU 中的一个项目,它是一个数学相关的科学计算库。
Part.II GSL 编译与安装
因为笔者使用的是 Windows 系统,在 Windows 下可以使用 『MSYS2 + Visual Studio』 对 GSL 进行安装和编译,也可以使用『CMake + Visual Studio』 对 GSL 进行安装和编译。前者已经有前辈写好了教程,下面主要针对后者的操作进行一下记录。
Chap.I GSL 的编译
这一步的目的是生成 GSL 动态库。
首先安装 cmake,VS等,然后需要查看 cmake 的路径是否添加到了系统变量path中。方法:我的电脑→右键属性→高级系统设置→环境变量→系统变量→path→添加 cmake.exe 的路径进去
下载最新版 gsl-2.7。然后解压在gsl-master目录下新建build文件夹
生成动态库
cmake -G"Visual Studio 16 2019" -DGSL_INSTALL_MULTI_CONFIG=ON -DNO_AMPL_BINDINGS=1 -DCMAKE_INSTALL_PREFIX=%cd%/install -DBUILD_SHARED_LIBS=ON -DMSVC_RUNTIME_DYNAMIC=ON A:/downloads/gsl-master
// 注意最后的路径是你自己的路径哦
编译gsl
cmake --build . --config Release --target install
// 生成 Release 版本的库
cmake --build . --config Debug --target install
// 生成 Debug 版本的库
得到所需文件
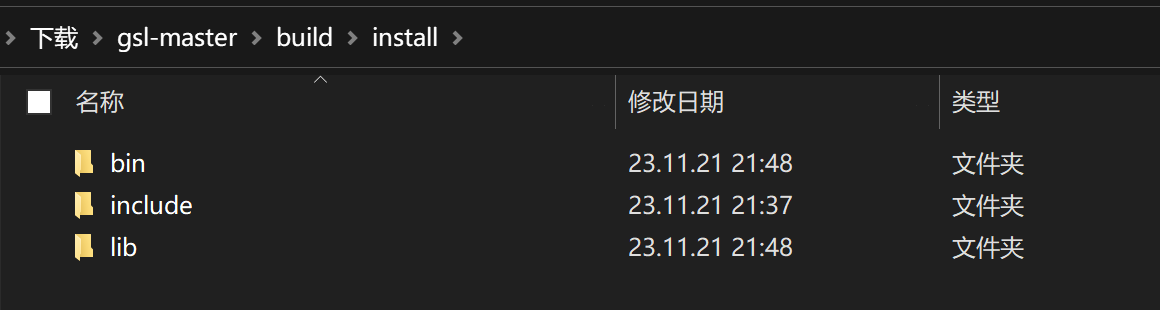
最后得到的文件树如下:
gsl
├─bin
│ ├─Debug
│ └─Release
├─include
│ └─gsl
└─lib
├─cmake
│ └─gsl-2.7
├─Debug
├─pkgconfig
└─Release
好像 Release 版本和 Debug 版本得到的东西是一样的。下面将介绍如何使用得到的这些库。
Chap.II 基于 VS 可视化操作的使用
新建一个项目,然后依次加入『附加包含目录』、『附加库目录』、『附加依赖项』
// 附加包含目录
A:\aWork\third-party\gsl\include
// 附加库目录
A:\aWork\third-party\gsl\lib\Release
// 附加依赖项
gsl.lib
gslcblas.lib
注意:dll 文件要加到工程目录,或者将其路径加入环境变量。
注意:如果一个项目要依赖其他项目,可以 选中项目→右键『属性』→VC++ 目录→包含目录和库目录把 GSL 的路径添加进去。
测试代码如下:
#include <stdio.h>
#include <gsl/gsl_matrix.h>
int main(void)
{
int i, j;
gsl_matrix* m = gsl_matrix_alloc(3, 3);
for (i = 0; i < 3; i++) {
for (j = 0; j < 3; j++) {
gsl_matrix_set(m, i, j, i + j);
}
}
for (i = 0; i < 3; i++) {
for (j = 0; j < 3; j++) {
printf("m(%d,%d) = %g\n", i, j, gsl_matrix_get(m, i, j));
}
}
gsl_matrix_free(m);
return 0;
}
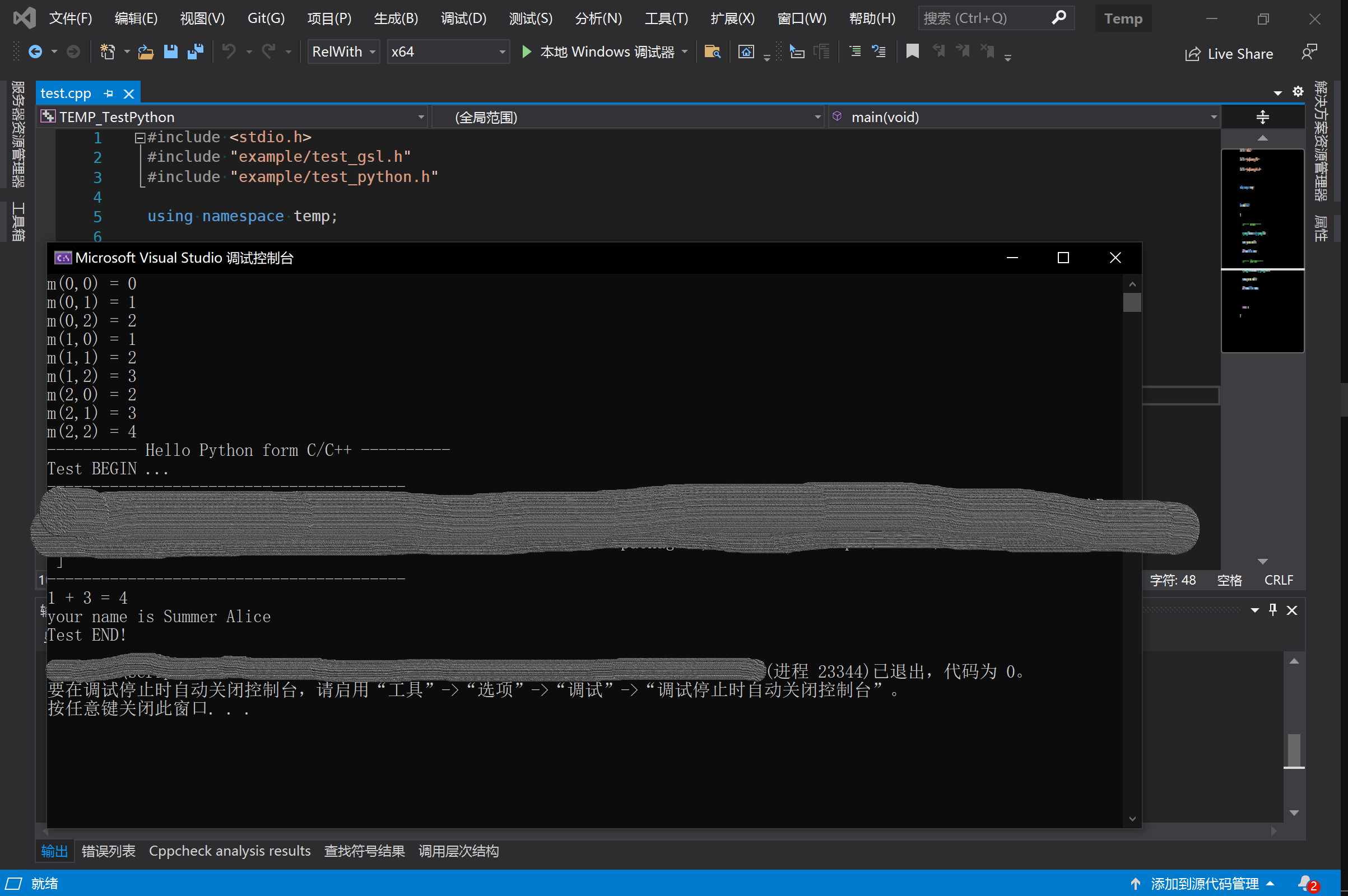
运行结果如下:

Chap.III 基于 CMake 的使用
基于 CMake 的使用其实和上面的差不多,就是“ 加入『附加包含目录』、『附加库目录』、『附加依赖项』”这几步操作变成了 CMake 语句,主要的语句为:
| CMake | 含义 | VS 操作 |
|---|---|---|
| include_directories / target_include_directories | 附加包含目录 | VS 右键『属性』→『C/C++』→『常规』→『附加包含目录』 |
| link_directories / target_link_directories | 附加库目录 | VS 右键『属性』→『链接器』→『常规』→『附加库目录』 |
| link_libraries / target_link_libraries | 附加依赖项 | VS 右键『属性』→『链接器』→『输入』→『附加依赖项』 |
最好用 target_xx ,因为它只会影响当前 target,而另一个会影响所有的 target。
因为文件比较多,不方便都放上来,感兴趣的朋友可以戳我下载(要钱的哦),文件树如下:
.
─app_test
│ ├─TEMP_TestGSL
│ └─TEMP_TestPython
├─LibGSL
│ ├─example
│ └─gexport
├─LibPython
│ ├─example
│ │ └─__pycache__
│ └─gexport
└─_doc
Part.III GSL 内置分布
Chap.I 一些常量
GSL_POSINF // +∞
GSL_NEGINF // -∞
GSL_NAN // NAN
GSL_POSZERO // +0
GSL_NEGZERO // -0
M_PI // PI
Chap.I gamma 分布
需包含头文件
#include <gsl/gsl_sf.h>
gsl_sf_gamma(a),计算得到 Γ ( a ) \Gamma(a) Γ(a), a a a 要大于 0gsl_sf_gamma_inc(a,x),计算得到不完全伽马函数 Γ ( a , x ) \Gamma(a,x) Γ(a,x)(其积分下限是 x x x)gsl_sf_gamma_inc_Q(a,x),计算得到归一化的不完全伽马函数 Q ( a , x ) Q(a,x) Q(a,x) ( Γ ( a , x ) Γ ( x ) \frac{\Gamma(a,x)}{\Gamma(x)} Γ(x)Γ(a,x))gsl_sf_gamma_inc_P(a,x),计算得到互补归一化的不完全伽马函数 P ( a , x ) = 1 − Q ( a , x ) P(a,x)=1-Q(a,x) P(a,x)=1−Q(a,x)
Chap.II t 分布
需包含头文件
#include <gsl/gsl_randist.h>
#include <gsl/gsl_cdf.h>
gsl_ran_tdist_pdf(x,n),计算得到自由度为 n,变量值为 x 的概率密度gsl_ran_tdist_pdf((x - mu) / sigma, n) / sigma,计算得到自由度为 n,变量值为 x,位置参数为 mu,标准差为 sigma 的gsl_cdf_tdist_P(x,n),计算得到自由度为 n 的 t 函数从负无穷到 x 的积分值;或者说得到自由度为 n,变量值为 x 的累积分布函数值gsl_cdf_tdist_Q(x,n), 1 − P ( x , n ) 1-P(x,n) 1−P(x,n)
关于位置尺度 t 分布
f
(
t
)
=
Γ
(
n
+
1
2
)
σ
π
n
Γ
(
n
2
)
(
1
+
(
t
−
μ
σ
)
2
n
)
−
n
+
1
2
f(t)=\frac{\Gamma\left( \frac{n+1}{2} \right) }{\color{red}\sigma\sqrt{\pi n}\ \Gamma\left( \frac{n}{2} \right)}\left( 1+\frac{\left(\color{red} {\frac{t-\mu}{\sigma}} \right)^2}{n} \right)^{-\frac{n+1}{2}}
f(t)=σπn Γ(2n)Γ(2n+1)(1+n(σt−μ)2)−2n+1
# python 代码
print(t.pdf(2,3,0,2)) # x, n, mu, sigam
print(t.pdf(1,3)/2) # x, n
可以用下面一行的代码,使得位置尺度 t 分布与通常意义上的 t 分布进行转换。
Chap.III 其他分布
- Laplace 分布:
gsl_ran_laplace_pdf(double x, double a)
GSL 只定义了稳定分布随机数生成,没有定义它的 pdf
double gsl_ran_levy(const gsl_rng * r, const double c, const double alpha);
double gsl_ran_levy_skew(const gsl_rng * r, const double c, const double alpha, const double beta);
Part.IV 随机数的生成
生成随机需要引用头文件#include <gsl/gsl_rng.h>
重要函数
- gsl_rng_uniform:返回一个在
[0,1)区间内的随机数 - gsl_rng_uniform_pos:返回一个在
(0,1)区间内的随机数 - gsl_ran_exponential:返回一个服从指数分布 1 μ e − x μ , x > 0 \frac{1}{\mu}e^{-\frac{x}{\mu}}, x>0 μ1e−μx,x>0 的随机数
Chap.I 报错的代码
下面的代码会报错,无法解析的外部符号 gsl_rng_default
#include <iostream>
#include <gsl/gsl_rng.h>
#include <gsl/gsl_randist.h>
int main()
{
gsl_rng* r;
int i, n = 10;
double low = 1;
double up = 10;
const gsl_rng_type* T;
gsl_rng_env_setup();
T = gsl_rng_default;
r = gsl_rng_alloc(T);
for (i = 0; i < n; i++)
{
double u = low + gsl_rng_uniform(r) * (up - low);
printf("%.5f\n", u);
}
gsl_rng_free(r);
return 0;
}
Chap.II 可以跑通的
#include <iostream>
#include <gsl/gsl_rng.h>
#include <gsl/gsl_randist.h>
using namespace std;
int main()
{
gsl_rng* rng;
const gsl_rng_type** r;
const gsl_rng_type** rngs = gsl_rng_types_setup();
double a = 1.85361, b = 0.612543, c = 3.78207, d = -0.749357;
for (r = rngs; *r != 0; r++)
{
rng = gsl_rng_alloc(*r);
double u = gsl_ran_levy_skew(rng, c, a, b);
cout << u << " " << rng->type->name << endl;
gsl_rng_free(rng);
}
cout << "---------------------------" << endl;
rng = gsl_rng_alloc(*rngs);
for (int i = 0; i < 10; i++)
{
double u = gsl_ran_levy_skew(rng, c, a, b);
cout << u << " " << rng->type->name << endl;
}
gsl_rng_free(rng);
getchar();
return 0;
}
Part.V 求积分
求积分需要引用头文件#include <gsl/gsl_integration.h>,下面是一些重要的函数的参数
- gsl_function:输入,GSL 函数,需要构造
- epsabs:输入,绝对误差,一般设为0
- epsrel:输入,相对误差,一般设为
1e-7 - limit:输入,子区间的最大数目
- gsl_integration_workspace:输入,积分寄存空间,子间隔及其结果存储在工作区提供的内存中
- result:输出,积分结果
- abserr:输出,绝对误差
- neval:不知道
Chap.I gsl_integration_qng
QNG算法是一种非自适应过程,它使用固定的Gauss-Kronrod-Patterson abscissae在最大87点处对被积函数进行采样。它提供了光滑函数的快速积分。函数原型如下:
int gsl_integration_qng(const gsl_function *f, double a, double b, double epsabs, double epsrel, double *result, double *abserr, size_t *neval)
示例:求积分 G = ∫ − 1 1 1 2 π e − x 2 2 d x G=\int_{-1}^{1}\frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}}dx G=∫−112π1e−2x2dx (标准正态分布)的值,已知 G = 0.6826 G=0.6826 G=0.6826。
#include <iostream>
#include <gsl/gsl_integration.h>
using namespace std;
double g1(double x, void* params)
{
double f = 1 / sqrt(2 * M_PI) * exp(-x * x / 2);
return f;
}
int main()
{
double a = -1, b = 1;
gsl_function gf;
gf.function = g1;
double r, er;
size_t n;
gsl_integration_qng(&gf, a, b, 1e-10, 1e-10, &r, &er, &n);
cout << r << endl;
return 0;
}
Chap.II gsl_integration_qag
QAG算法是一种简单的自适应积分算法。将积分区域划分为子区间,在每次迭代中对估计误差最大的子区间进行等分。这可以迅速降低总体误差,因为子区间集中在被积函数的局部困难周围。其函数原型如下:
int gsl_integration_qag(const gsl_function *f, double a, double b, double epsabs, double epsrel, size_t limit, int key, gsl_integration_workspace *workspace, double *result, double *abserr)
Chap.III gsl_integration_qags
当积分区域中存在可积奇点时,自适应程序将在奇点周围集中新的子区间。随着子区间的减小,积分的连续逼近以极限方式收敛。这种接近极限的方法可以使用外推过程来加速。QAGS算法将自适应二分法与Wynn - epsilon算法相结合,加快了对多种可积奇点的积分速度。其函数原型如下:
int gsl_integration_qags(const gsl_function *f, double a, double b, double epsabs, double epsrel, size_t limit, gsl_integration_workspace *workspace, double *result, double *abserr)
示例:求积分 G = ∫ 0 1 x − 1 2 l o g ( α x ) d x G=\int_{0}^{1}x^{-\frac{1}{2}}log(\alpha x)dx G=∫01x−21log(αx)dx 的值,已知 α = 1 \alpha=1 α=1时, G = − 4 G=-4 G=−4。
#include <stdio.h>
#include <math.h>
#include <gsl/gsl_integration.h>
double f(double x, void* params) {
double alpha = *(double*)params;
double f = log(alpha * x) / sqrt(x);
return f;
}
int
main(void)
{
gsl_integration_workspace* w
= gsl_integration_workspace_alloc(1000);
double result, error;
double expected = -4.0;
double alpha = 1.0;
gsl_function F;
F.function = &f;
F.params = α
gsl_integration_qags(&F, 0, 1, 0, 1e-7, 1000,
w, &result, &error);
printf("result = % .18f\n", result);
printf("exact result = % .18f\n", expected);
printf("estimated error = % .18f\n", error);
printf("actual error = % .18f\n", result - expected);
printf("intervals = %zu\n", w->size);
gsl_integration_workspace_free(w);
getchar();
return 0;
}
Chap.IV gsl_integration_qagp
其函数原型如下:
int gsl_integration_qagp(const gsl_function *f, double *pts, size_t npts, double epsabs, double epsrel, size_t limit, gsl_integration_workspace *workspace, double *result, double *abserr)
Chap.V gsl_integration_qagi
计算(-∞,+∞)的积分,其函数原型如下:
int gsl_integration_qagi(gsl_function *f, double epsabs, double epsrel, size_t limit, gsl_integration_workspace *workspace, double *result, double *abserr)
Chap.VI gsl_integration_qagiu
计算(a,+∞)的积分, 其函数原型如下:
int gsl_integration_qagiu(gsl_function *f, double a, double epsabs, double epsrel, size_t limit, gsl_integration_workspace *workspace, double *result, double *abserr)
Chap.VII gsl_integration_qagil
计算(-∞,b)的积分,其函数原型如下:
int gsl_integration_qagil(gsl_function *f, double b, double epsabs, double epsrel, size_t limit, gsl_integration_workspace *workspace, double *result, double *abserr)
Reference
GCC、GNU到底啥意思? ↩︎







![[linux初阶][vim-gcc-gdb] TwoCharter: gcc编译器](https://img-blog.csdnimg.cn/direct/8f17326e3e0b463eb224d0ef5f033db5.png)
![[SWPUCTF 2021 新生赛]crypto5(小明文攻击)](https://img-blog.csdnimg.cn/direct/adf436ec4b2248d59dc7aacad1b4f9ea.png)