一、概述
链式前向星是一种用于存储图的数据结构,特别适合于存储稀疏图,它可以有效地存储图的边和节点信息,以及边的权重。
它的主要思想是将每个节点的所有出边存储在一起,通过数组的方式连接(类似静态数组实现链表)。这种方法的优点是存储空间小,查询速度快,尤其适合于处理大规模的图数据,在一些笔试或者竞赛的场景中经常使用。
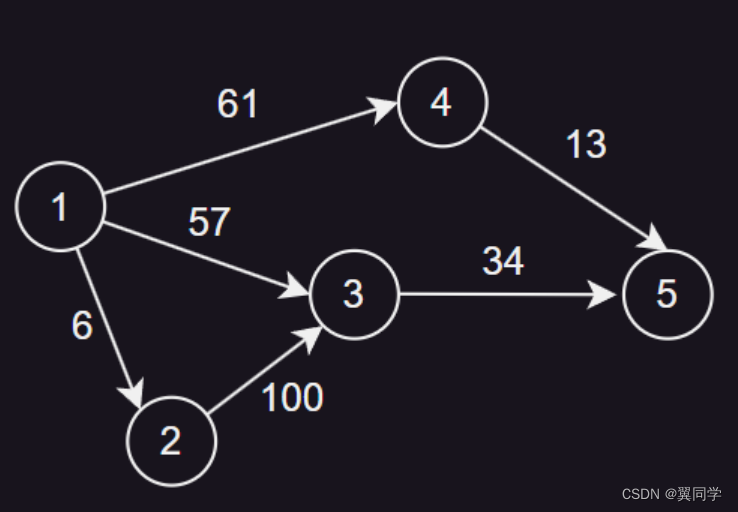
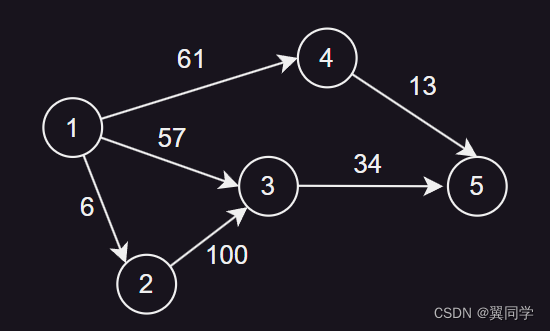
下面,我们用这张图来图解一下链式前向星的存储逻辑:
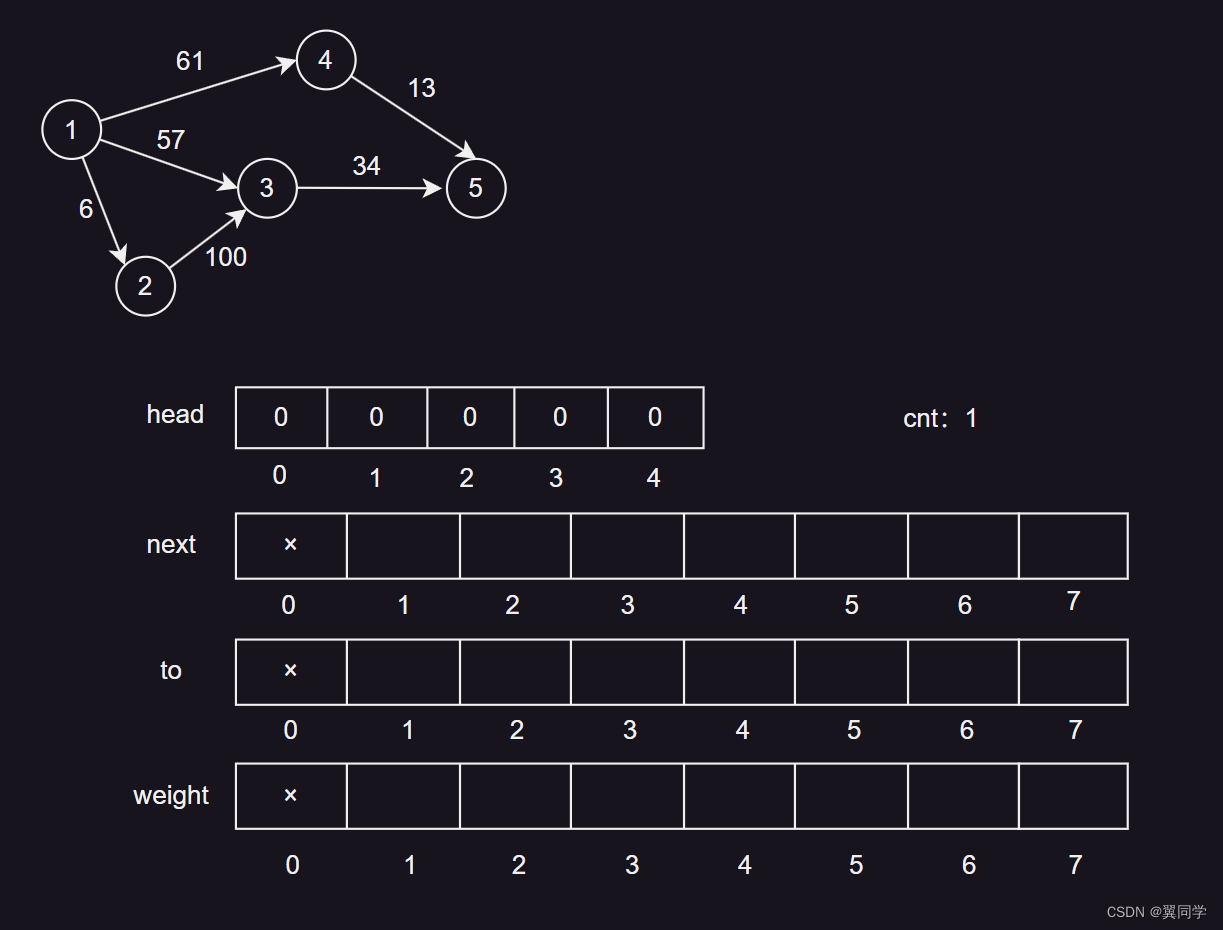
二、前置准备
注意看这里的设定,以及我加粗的提示。
-
head数组:head[i]存储的是节点i的第一条边的编号。这样,我们可以通过head[i]快速找到从节点i出发的所有边。 -
next数组:next[j]存储的是编号为j的边的下一条边的编号。这样,我们可以通过next[j]快速找到从同一个节点出发的下一条边。 -
to数组:to[j]存储的是编号为j的边的终点节点编号。这样,我们可以通过to[j]快速找到边j的终点,也就是这条边要去往哪里。 -
weight数组:weight[j]存储的是编号为j的边的权重。这样,我们可以通过weight[j]快速找到边j的权重。 -
cnt变量:cnt用于存储边的数量,也表示边的编号。每添加一条边,cnt就会增加1。这样,我们可以通过cnt快速知道当前图中边的数量,同时我们也认为cnt是新添加边的编号。
三、初始化
public static void build(int n) {
cnt = 1; // 边从1开始编号
Arrays.fill(head, 1, n + 1, 0); // head[1 ... n] 全设为 0
}
在链式前向星中,我们使用cnt来作为边的编号,由于边的编号是从1开始的,所以初始化时我们将cnt设置为1。同时,将head数组的所有元素设置为0。因为head[i]存储的是节点i的第一条边的编号,所以,如果节点i没有出度(即没有从节点i出发的边),那么head[i]就应该为0。初始化时所有节点都没有出度,后续在添加边的时候,会更新对应的head[i]的值。
四、添加边(重点)
在链式前向星中添加边的操作是最核心的,它涉及到head、next、to、weight数组的更新,以及边的编号cnt的自增。
在看代码之前,我们先回顾一下各个结构的下标以及值的含义:
-
head数组:下标i表示节点编号,值head[i]表示从节点i出发的第一条边的编号。 -
next数组:下标j表示边的编号,值next[j]表示编号为j的边的下一条边的编号。 -
to数组:下标j表示边的编号,值to[j]表示编号为j的边的终点节点编号。 -
weight数组:下标j表示边的编号,值weight[j]表示编号为j的边的权重。
结合上述含义,我们来看代码就很清晰了:
// (u, v, w): 有一条边,从u节点指向v节点,权重为w
// 在每一次添加边时,cnt都表示当前未分配的边的编号,添加边后cnt需++
public static void addEdge(int u, int v, int w) {
next[cnt] = head[u];
to[cnt] = v;
weight[cnt] = w;
head[u] = cnt;
++cnt;
}
首先,我们需要更新next数组。next[cnt]存储的是编号为cnt的边的下一条边的编号。在添加新边时,我们将新边的next置为旧的头边号head[u],这样就可以通过next[cnt]快速找到从节点u出发的下一条边。
然后,我们需要更新to数组,将新边的终点设置为v,这样就可以通过to[cnt]快速找到边cnt的终点。
更新weight数组也很自然,就是将新边的权重设置为w,最后,我们将节点u的头边号修改为当前新边的编号,这样就可以通过head[u]快速找到从节点u出发的第一条边。
备注:记得每添加一条边,边的编号
cnt就需要增加1
五、建图
建图分为有向图与无向图,输入的参数是一个二维数组edges作为输入,这个数组的每个元素都是一个长度为3的数组,代表一条边的两个端点和这条边的权重。
// 建有向图
public static void directGraph(int[][] edges) {
for (int[] edge : edges) {
addEdge(edge[0], edge[1], edge[2]); // 添加有向边
}
}
// 建无向图
public static void undirectGraph(int[][] edges) {
for (int[] edge : edges) {
addEdge(edge[0], edge[1], edge[2]); // 添加边
addEdge(edge[1], edge[0], edge[2]); // 添加反向边
}
}
六、图解
下面这个数组提供了图的边信息,基本上题目都会给定形式的信息,让你去建图:
有一条边(u, v, w),表示从u节点指向v节点,权重为w
[
[1, 6, 2],
[1, 3, 57],
[1, 4, 61],
[2, 3, 100],
[3, 5, 34],
[4, 5, 13],
]
这里 u,v,w 的含义以及顺序应根据具体题目具体分析,这里的设定是(u, v, w)表示一条边从u节点指向v节点,权重为w。
// 添加边:
public static void addEdge(int u, int v, int w) {
next[cnt] = head[u];
to[cnt] = v;
weight[cnt] = w;
head[u] = cnt;
++cnt;
}
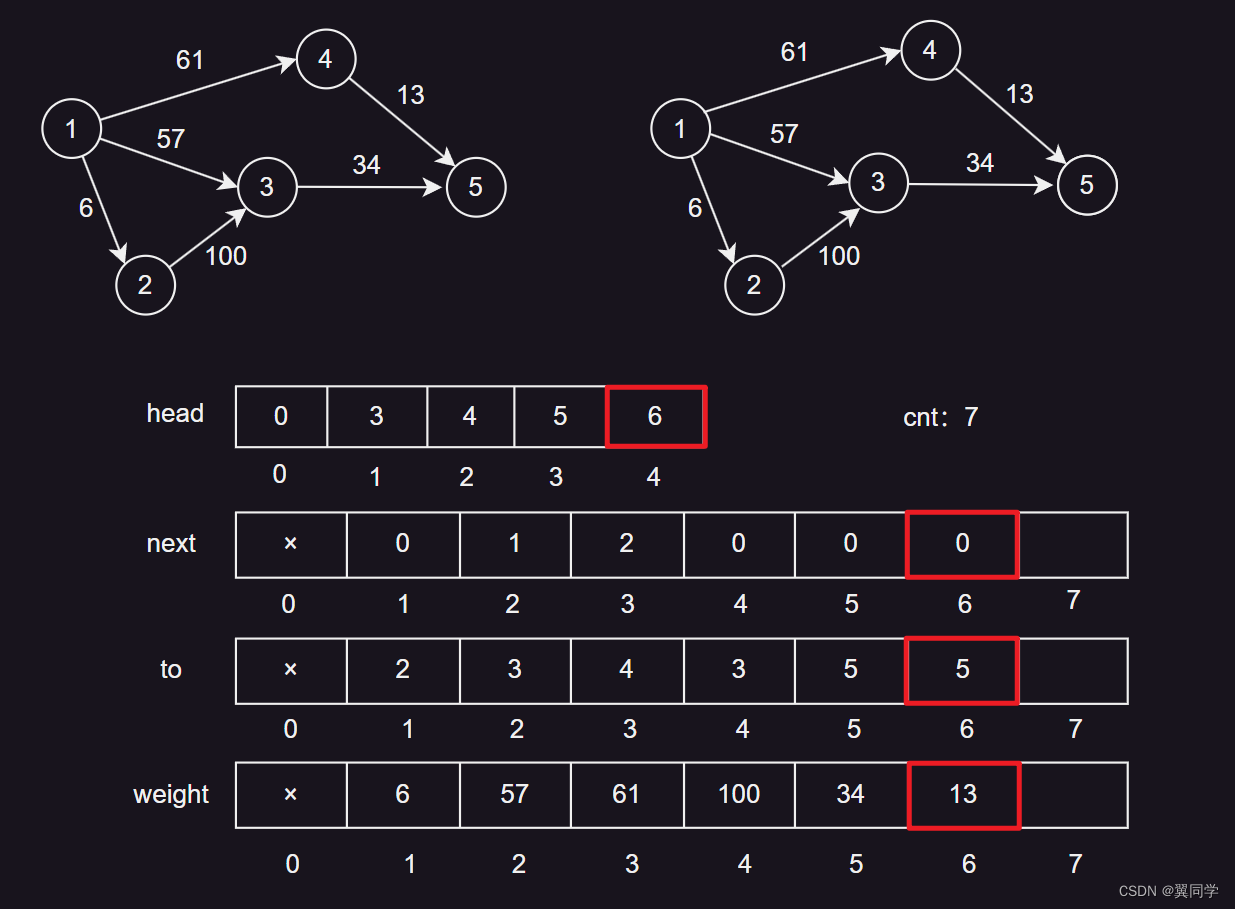
下面我们图解一下,在链式前向星中,依次添加6条边到有向图中的逻辑。

如果看不懂,建议返回上面去看各个数组的下标以及值的含义。
添加边 {1, 6, 2}
head[1] = 1:节点1的第一条边的编号是1。next[1] = 0:边1没有下一条边。to[1] = 2:边1的终点是节点2。weight[1] = 6:边1的权重是6。cnt:2,表示当前边的数量是1,下一条边的编号是2。
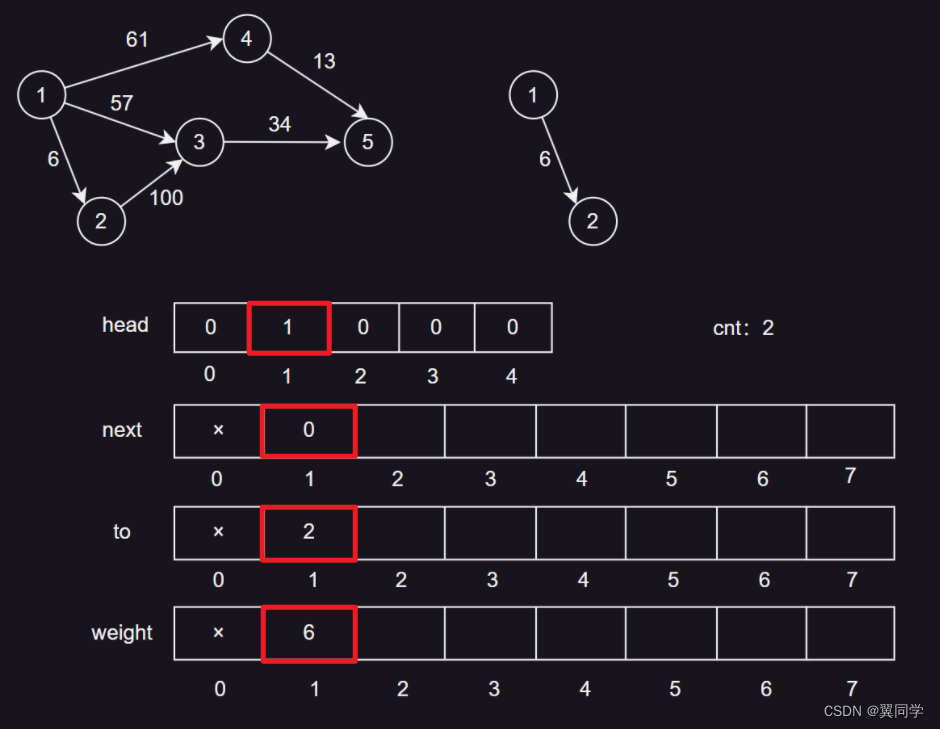
添加边 {1, 3, 57}
head[1] = 2:节点1的第一条边的编号是2。next[2] = 1:边2的下一条边是边1。to[2] = 3:边2的终点是节点3。weight[2] = 57:边2的权重是57。cnt:3,表示当前边的数量是2,下一条边的编号是3。
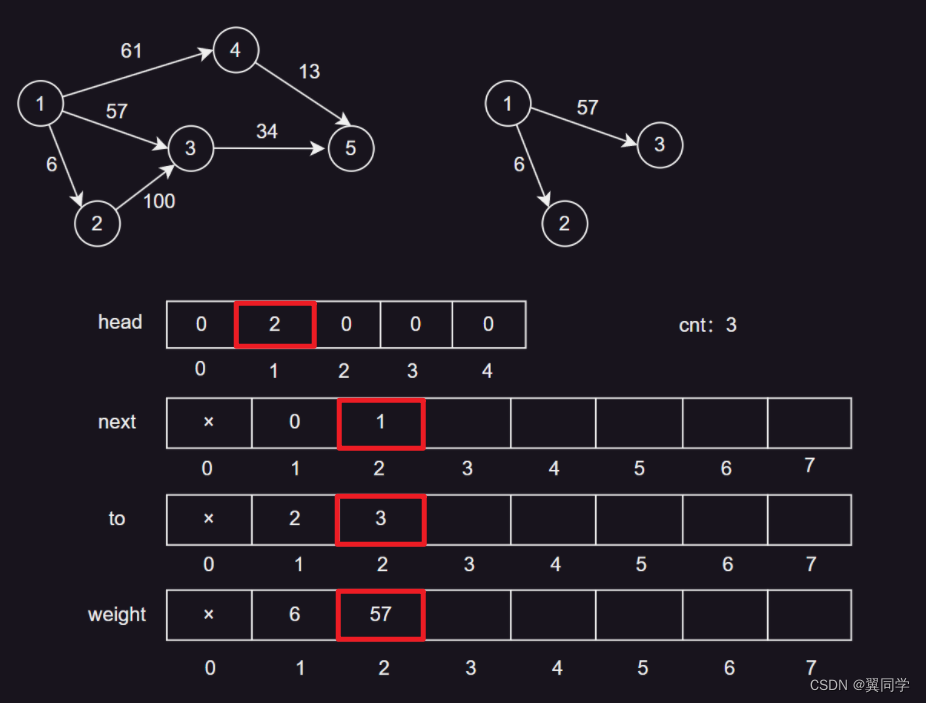
添加边 {1, 4, 61}
head[1] = 3:节点1的第一条边的编号是3。next[3] = 2:边3的下一条边是边2。to[3] = 4:边3的终点是节点4。weight[3] = 61:边3的权重是61。cnt:4,表示当前边的数量是3,下一条边的编号是4。
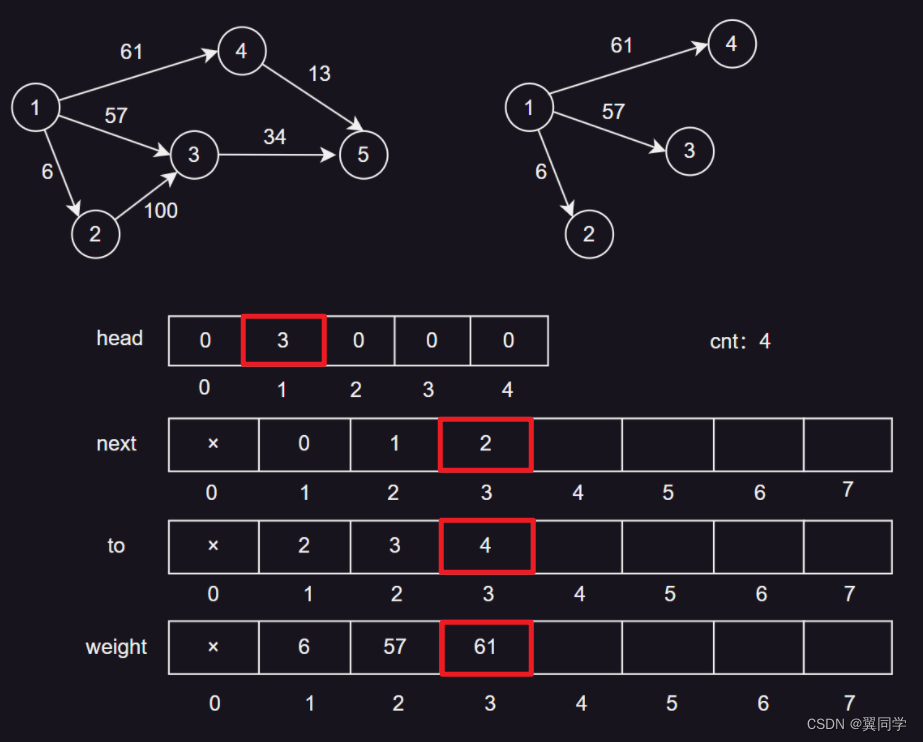
添加边 {2, 3, 100}
head[2] = 4:节点2的第一条边的编号是4。next[4] = 0:边4没有下一条边。to[4] = 3:边4的终点是节点3。weight[4] = 100:边4的权重是100。cnt:5,表示当前边的数量是4,下一条边的编号是5。
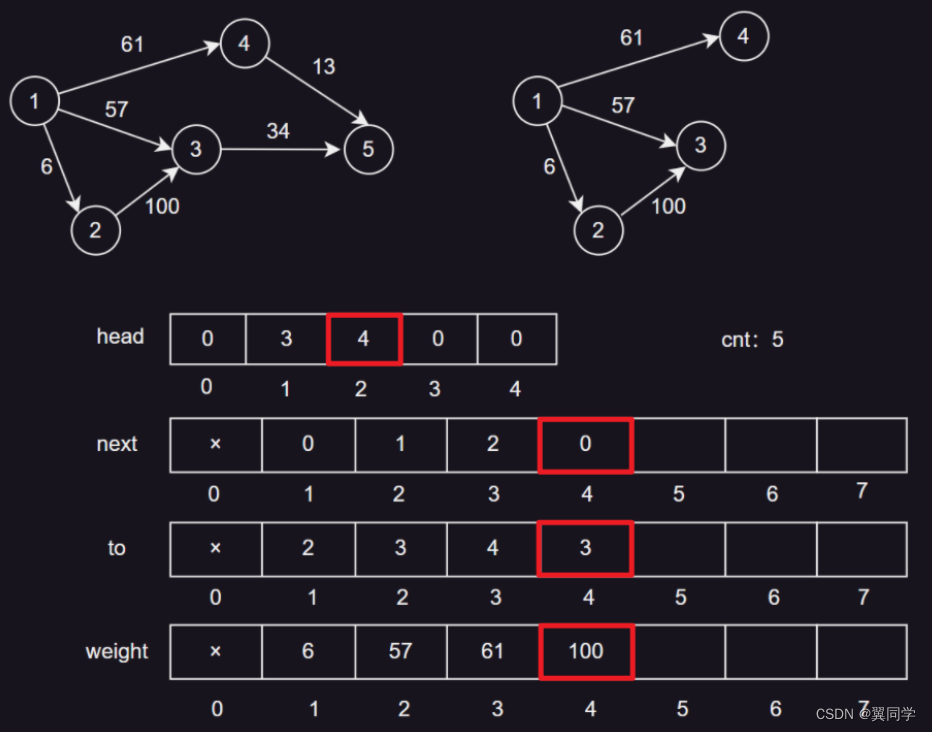
添加边 {3, 5, 34}
head[3] = 5:节点3的第一条边的编号是5。next[5] = 0:边5没有下一条边。to[5] = 5:边5的终点是节点5。weight[5] = 34:边5的权重是34。cnt:6,表示当前边的数量是5,下一条边的编号是6。
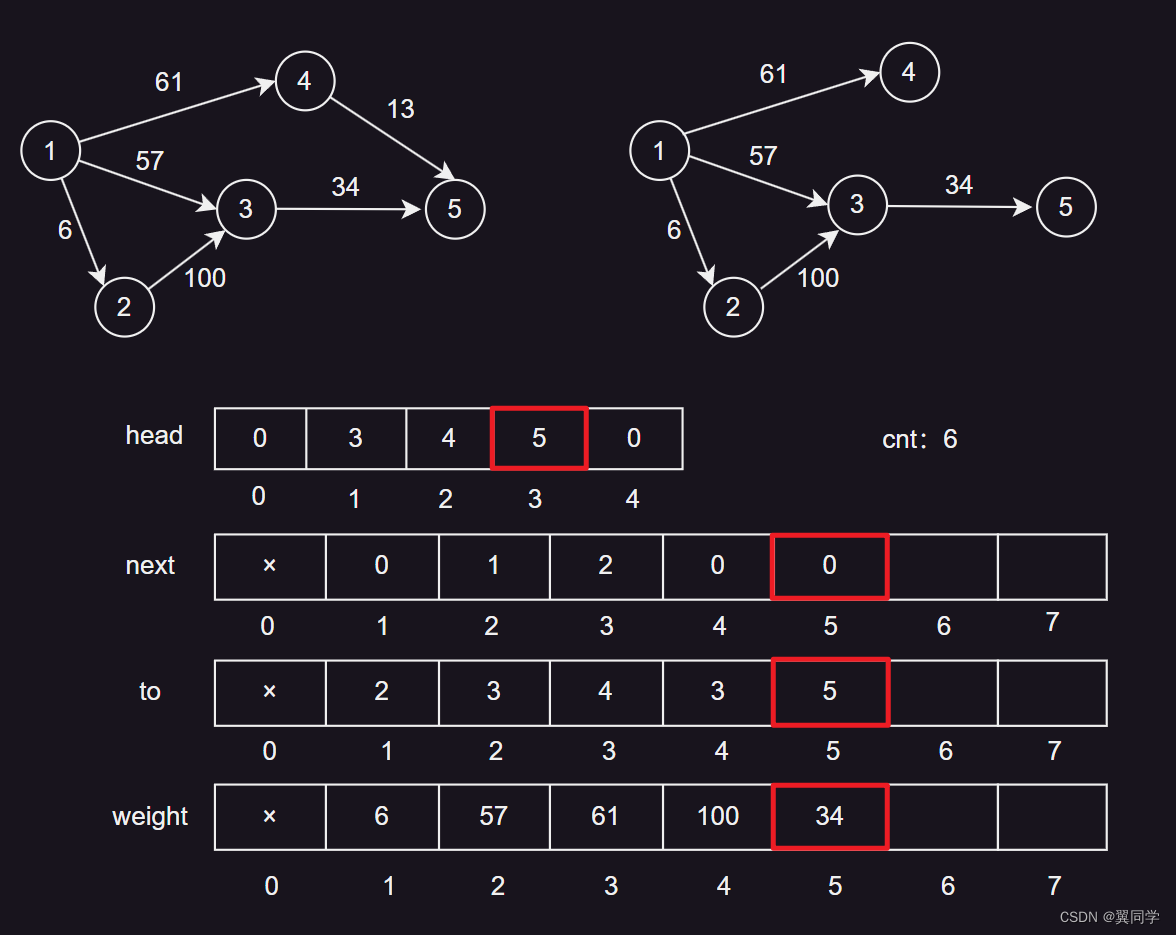
添加边 {4, 5, 13}
head[4] = 6:节点4的第一条边的编号是6。next[6] = 0:边6没有下一条边。to[6] = 5:边6的终点是节点5。weight[6] = 13:边6的权重是13。cnt:7,表示当前边的数量是6,下一条边的编号是7。
七、遍历图
遍历图的逻辑也不难理解,就是对于每个节点,遍历其所有的邻居,根据next数组不断去拿到和每个节点连接的边的编号,直到没有邻居节点为止,一步步跳着找嘛。
步骤如下:
- 对于每个节点,通过
head数组找到该节点的第一条边。 - 通过
next数组找到下一条边,直到next数组的值为0,表示没有更多的边。 - 在遍历过程中,可以通过
to和weight数组获取边的终点和权重。
我们用打印邻居节点的方式来验证遍历的结果:
public static void traversal(int n) {
StringBuilder sb = new StringBuilder();
sb.append("链式前向星遍历,u: (v, w)表示u有一条边前往v,权重为w\n");
for (int i = 1; i <= n; i++) {
sb.append("[").append(i).append("]: ");
for (int ei = head[i]; ei > 0; ei = next[ei]) {
sb.append("(").append(to[ei]).append(",").append(weight[ei]).append(") "); // 输出边的终点和权重
}
sb.append("\n");
}
System.out.println(sb.toString()); // 打印结果
}
八、完整代码
package cn.zhengyiyi;
import java.util.Arrays;
public class Main {
public static int N = 11;
public static int M = 21;
/**
* 编号为 i 的节点,其第一条边的编号为 head[i]
* 备注:如果 head[i] 为0,说明没有一条边从节点 i 出发
*/
public static int[] head = new int[N];
/**
* 编号为 i 的边,它的下一条边是 next[i],
*/
public static int[] next = new int[M];
/**
* 编号为 i 的边,前往的节点是 to[i],也就是第 i 条边的终点是 to[i]
*/
public static int[] to = new int[M];
/**
* 编号为 i 的边,权重是 weight[i]
*/
public static int[] weight = new int[M];
/**
* 记录边的数量,初始时值为 1
*/
public static int cnt;
// 初始化链式前向星
public static void build(int n) {
cnt = 1; // 边从1开始编号
Arrays.fill(head, 1, n + 1, 0); // head[1 ... n] 全设为 0
}
// 添加一条边:(u->v,权重为w)
public static void addEdge(int u, int v, int w) {
// 1. 更新next数组,将新边的next置为旧的头边号head[u],方便后续跳到旧的头边号
next[cnt] = head[u];
// 2. 更新to数组,设置当前新边的终点为v
to[cnt] = v;
// 3. 更新weight数组,设置当前边的权重w
weight[cnt] = w;
// 4. 更新head数组,将原先的头边号修改为当前新边
head[u] = cnt;
// 5. 最后边的编号要自增
++cnt;
}
// 建立有向图
public static void directGraph(int[][] edges) {
for (int[] edge : edges) {
addEdge(edge[0], edge[1], edge[2]); // 添加有向边
}
}
// 建立无向图
public static void undirectGraph(int[][] edges) {
for (int[] edge : edges) {
addEdge(edge[0], edge[1], edge[2]); // 添加边
addEdge(edge[1], edge[0], edge[2]); // 无向图需要添加反向边
}
}
// 遍历图
public static void traversal(int n) {
StringBuilder sb = new StringBuilder();
sb.append("链式前向星遍历,u: (v, w)表示u有一条边前往v,权重为w\n");
for (int i = 1; i <= n; i++) {
sb.append("[").append(i).append("]: ");
for (int ei = head[i]; ei > 0; ei = next[ei]) {
sb.append("(").append(to[ei]).append(",").append(weight[ei]).append(") "); // 输出边的终点和权重
}
sb.append("\n");
}
System.out.println(sb.toString()); // 打印结果
}
public static void main(String[] args) {
int n = 5; // 节点数
build(n); // 初始化
int[][] directEdges = { // 有向图的边
{ 1, 6, 2 },
{ 1, 3, 57 },
{ 1, 4, 61 },
{ 2, 3, 100 },
{ 3, 5, 34 },
{ 4, 5, 13 }
};
directGraph(directEdges); // 建立有向图
traversal(n); // 遍历有向图
}
}
运行结果:
链式前向星遍历,u: (v, w)表示u有一条边前往v,权重为w
[1]: (4,61) (3,57) (6,2)
[2]: (3,100)
[3]: (5,34)
[4]: (5,13)
[5]: