关于柔性阵列(/三维阵列)波束形成的仿真实践以及稳健波束形成的思考(1)

说明

关于波束形成，我之前写过几篇相关的博文，如参考资料[1]、[2]、[3]。除去在博文[2]中有讨论过阵元相对位置关系对波束形成的影响：“如何基于遗传算法优化阵元相对位置关系以压低旁瓣峰值”以外，似乎我认知里的天线阵列，在设计完成后其相对位置关系是不会发生变化的。事实上在绝大多数情况下确实是这样：比如车载雷达中我们的天线都是一个射频板上，它是一个刚体结构，当雷达制作好后，不存在在使用过程中发生天线相对位置关系变化的情况。

但，还是有的，而且有多种可能的应用场景。特别是在声呐中应用较多，如参考资料[4],有了这样的一个概念(在应用过程中，阵列相对位置关系是可能发生变化的)之后，关于所谓的柔性阵列就能很容易理解了：如果雷达的阵列天线和后端的接收处理模块是分开的，且各自装配在了不同的位置，并各自有一定的自由度，那么在使用的过程中就极可能发生相对位置的改变。

试想一个二维面阵在XOY平面上，阵列中每个天线的位置都可能在x方向、y方向乃至z方向发生变化。这种情况下其波束形成的结果是什么样的？以及我们可以采取什么手段来消除这种相对位置畸变带来的不良影响？这两个话题是本博文想要探讨的。

Blog

2024.3.28 博文第一次撰写

一、柔性阵列概述

所谓的柔性阵列，顾名思义就是阵列是柔软的、可以发生形变的。我在前文说明中做了一点解释，读者可以自行在相关论文网站上搜索柔性阵列以获得更多的信息。更形象地，如下述两图所示：

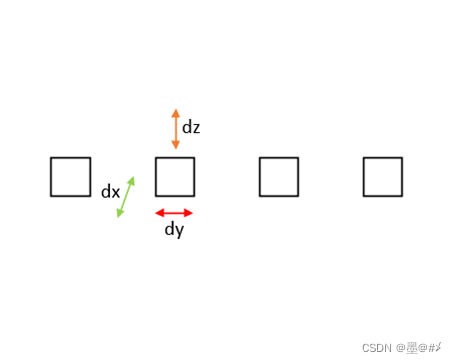
图1.1 柔性线阵阵元位置变化示意图

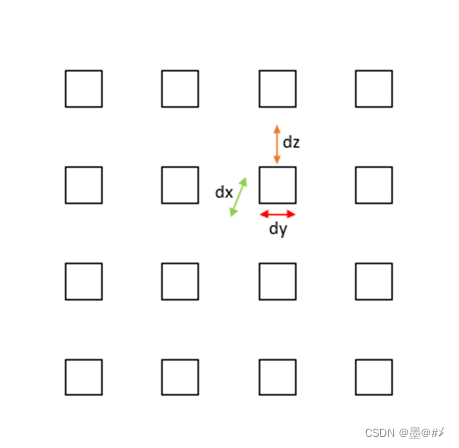
图1.2 柔性面阵阵元位置变化示意图

上面两图所示的变化dx、dy、dz可以针对每个阵元。可能上面两张图有点抽象…，总之想表达的意思就是：在柔性阵列中，每个阵元的位置在不同的时刻会在一定的自由度和一定的范围内变化(这种变化可能是随机的、也可能是有规律的)。后文将分别探讨线阵和面阵下给阵元位置加随机扰动的波束方向图结果。

二、波束形成概述

关于波束形成(这里特指发射端)，我在博文[1] 关于阵列发射端的波束形成(相控阵)研究与仿真实践-CSDN博客中表述得很清楚，这里不做过多的原理上的解释，本质上，阵列的方向图就是基于各阵元所辐射电磁波的初始相位、幅值、以及它们之间的相对位置关系来求得各个方向下电磁波叠加后的结果。为简化仿真，本文讨论的阵元都是无方向性的。给出面阵下阵列因子的表达式：

对于N*M阵元面阵【对于线阵，我们抛开其中一个维度的累加即可】：

（2-1）

式中为方向各阵元波束叠加后的幅值，为第n行m列的阵元的辐射强度(幅值)，为该阵元的初始相位，Dn为列向第n个阵元相对参考阵元(比如我们以第一行第一列的阵元为参考阵元)的距离，Dm为行向第m个阵元相对参考阵元的距离。θ、φ的定义如下图所示：

图2.1 阵列坐标系示意图

我们把阵列排布在XOZ平面(在后文的仿真中也是这样)，此时，θ为目标方向与阵列参考点连线在xoy平面的投影与y轴的夹角，φ为目标方向连线与xoy平面的夹角。

不难理解的是：

对于一维线阵，如果阵元只在阵列所在直线上变化，则畸变前后都还是线阵；如果同时只在两个维度发生变化，则畸变后我们需要以面阵对它进行讨论；而如果在三个维度同时变化，此时阵列变成了三维的了！

对于二维面阵，如果阵元发生了在垂直于面阵所在平面的变化，则阵列也变成了三维的！

【当阵列变成三维的时，我首先想到的是之前了解到大陆ARS548雷达采用了波导腔体天线，其阵列排布貌似也是三维的。不过其阵列是固化的，所以它三维排布的阵列的相对位置关系并不会随时间变化，在做角度测量时补偿相位即可，但是如果阵列在使用的过程中相对位置关系会随着时间变化，测角的难度会极大地提高。】

公式(2-1)中给出的只是面阵的阵列因子表达式，经过前面的分析我们知道，本文要解决的问题还需要再拓展一个维度。这里以线阵在第三维度的变化来分析这个问题：

图2.2 阵列阵元发生深度(第三)维度变化时的示意图

图中特意说了y方向，读者可以结合图2.1理解。图中，我们假设B阵元从原来的位置(蓝色)发生了dy的位置畸变，变换到了红色所在位置。假设目标（水平）角度为θ，则由图中几何关系可知：相较于原来波束从A到B（蓝色位置）的相位差：

(2-2)

此时的相位差变成了：

(2-3)

或：

(2-4)

我们定义阵元B下移时dy为负，上移时dy为正。这里是以前一个阵元为参考得到的相位差，更加通用的公式里我们还是要以同一个阵元(比如起始阵元)做参考。为构建三维阵列下通用的阵列因子表达式，基于(2-4)的结论，此时我们需要改写公式(2-1):

(2-5)

式中，我们引入了dy导致的相位差，从而将二维阵列的阵列因子表达式变成了三维的。后文的仿真，不管对于线阵还是面阵，我们都以上式作为基准。

三、柔性线阵波束方向图仿真结果与探讨

本章中仿真的基本参数列表如下：

表3.1 柔性阵列波束方向图仿真参数列表

参数	值
阵元个数	8
阵列类型	间隔0.5个波长的均匀线阵
载波频率	77GHz
X方向畸变范围	±0.25*λ(为了保证相邻阵元的位置不会“互换”)
Z方向畸变范围	±5*λ
Y方向畸变范围	±2.5*λ
畸变方法	每个阵元的畸变相对独立，在各个方向的畸变范围内随机产生畸变。
预设各阵元幅值	1
预设各阵元初始相位	0 【我在代码中也提供了不同角度下初始相位的设置方法，读者只需更改角度，即可计算得到特定角度下各阵元的初始相位值】

3.1 只在x方向发生畸变

畸变前后的相对位置关系如下图所示:

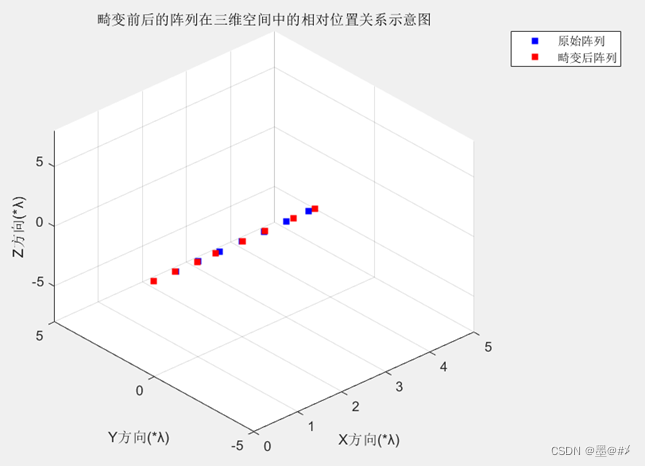
图3.1 X方向畸变前后阵列位置关系图(1)

图3.2 X方向畸变前后阵列位置关系图(2)

在前述阵列下，得到波束方向图的仿真结果：

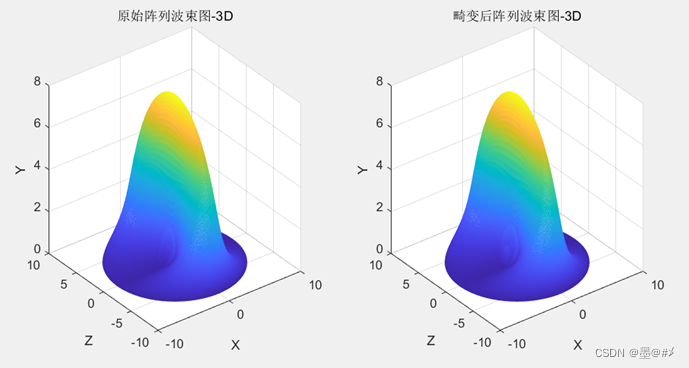
图3.3 X方向畸变前后阵列波束图对比(1)

上图中将波束映射到了空间坐标系中，映射前长这样：

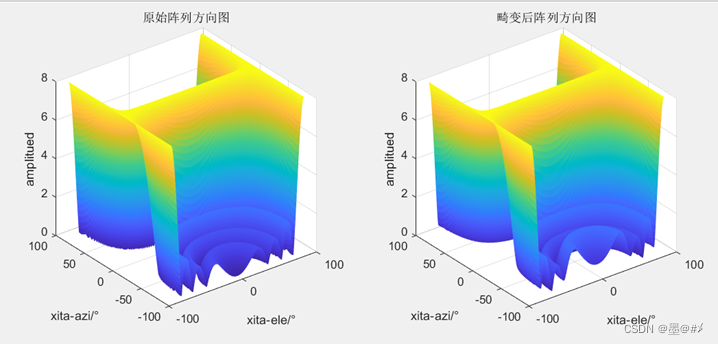
图3.4 X方向畸变前后阵列波束图对比(2)

【需要说明的是：这里与之前博文[1]：关于阵列发射端的波束形成(相控阵)研究与仿真实践-CSDN博客中的不一样，在[1]中，我认为线阵下，不同俯仰角度的波束方向图应该是一样的，所以在代码中我求得俯仰为0°方向的波束图后直接repmat到全部的俯仰维度，在那样的处理下，俯仰向的角度选择就不符合图2.1了，这里对那篇博文做一个更正说明，后续应该以本博文为准】

取出水平向和俯仰向两个切片进行观察：

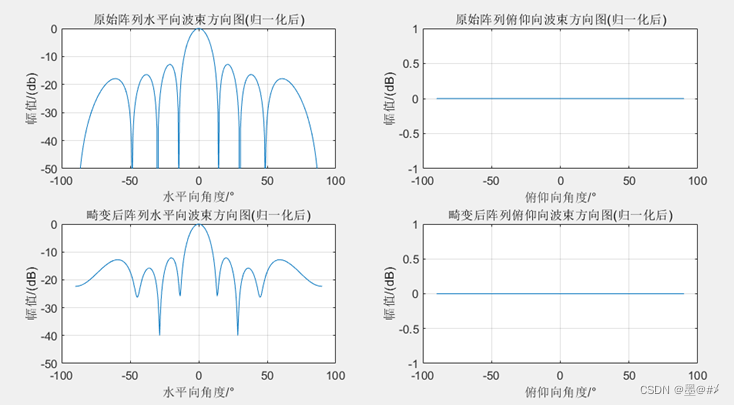
图3.5 X方向畸变前后阵列波束图对比(3)

从上面几幅图的仿真结果来看，在x方向的畸变并不会对主波束产生影响。仿真的结果符合预期：比如因为阵列是在x方向上排布的，所以应该在水平向(x方向)有更窄的波束宽度。

3.2 只在Z方向发生畸变

畸变前后的相对位置关系如下图所示:

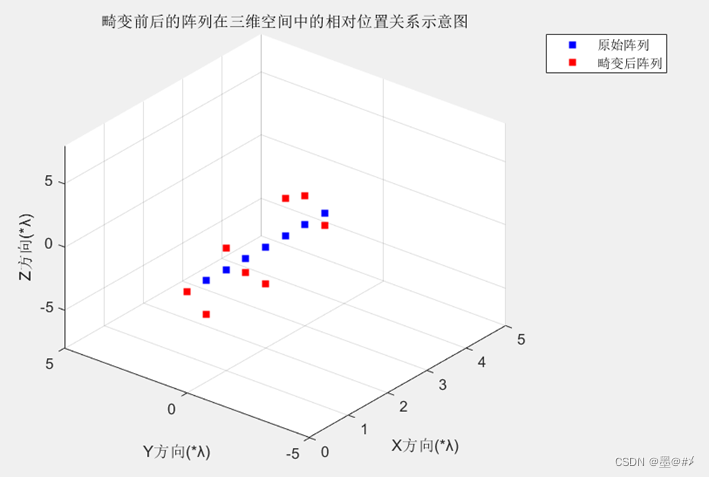
图3.6 Z方向畸变前后阵列位置关系图(1)

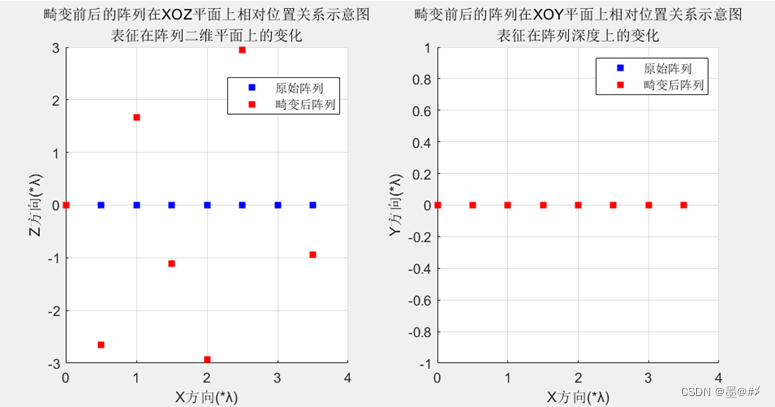
图3.7 Z方向畸变前后阵列位置关系图(2)

在前述阵列下，得到波束方向图的仿真结果：

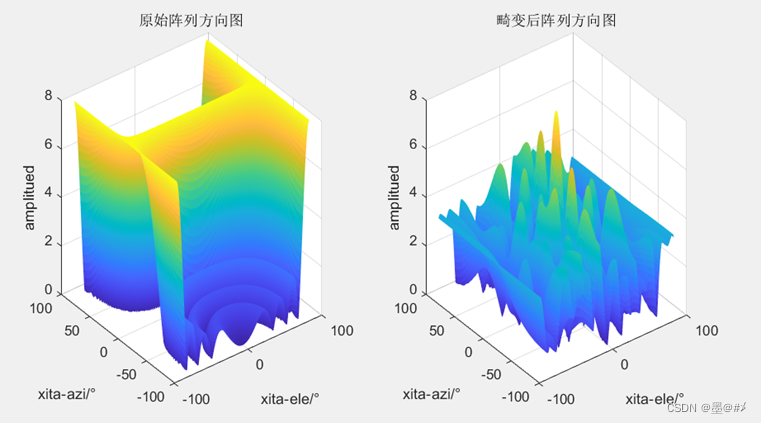
图3.8 Z方向畸变前后阵列波束图对比(1)

将之映射到空间坐标系并分别取水平、俯仰向两个切片：

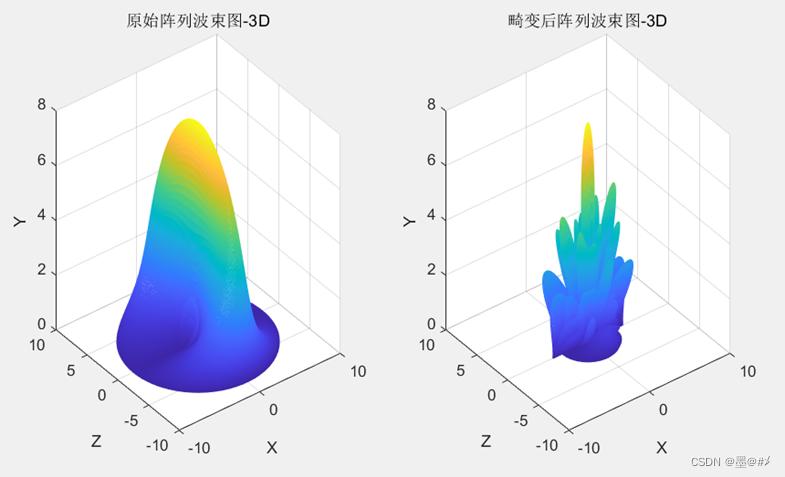
图3.9 Z方向畸变前后阵列波束图对比(2)

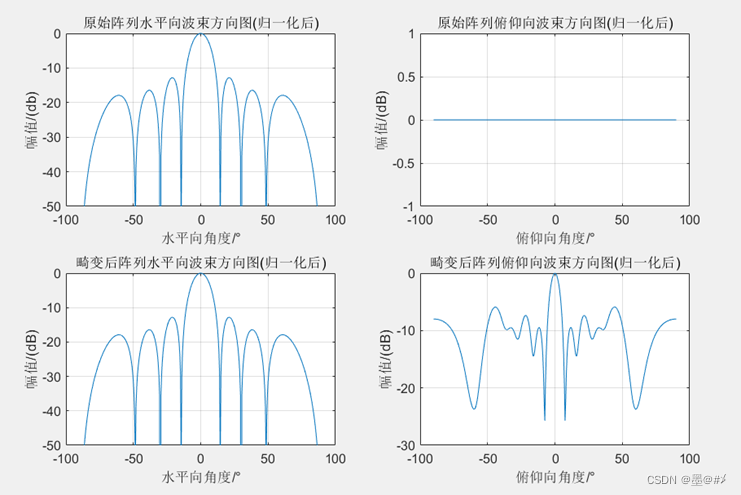
图3.10 Z方向畸变前后阵列波束图对比(3)

由前面几幅图可知，当在Z方向发生畸变时，此时阵列实际上已经变成了二维面阵，不过X方向孔径没有变化，所以在X方向上波束宽度还是很窄，但是由于在Z方向有孔径，所以可以看到其在俯仰向的幅值不再是一样的。Z方向的畸变也不会影响主波束的指向，但是旁瓣会增加，且幅度很高。

3.3 只在Y方向发生畸变

Y方向在本博文预先设置的坐标系中，属于“深度”方向。其畸变前后的阵列排布如下图所示：

图3.11 Y方向畸变前后阵列位置关系图(1)

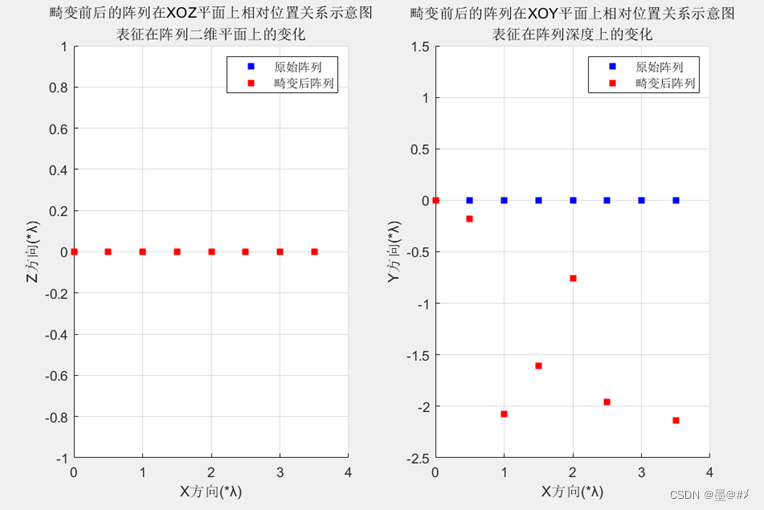
图3.12 Y方向畸变前后阵列位置关系图(2)

(因为在得到新阵列时以第一个阵元为基准做了对齐，所以有时候若第一个阵元的变化值比较大，是可能存在上图中全部的变化方向都往下的情况)，在前述阵列下，得到的波束方向图如下：

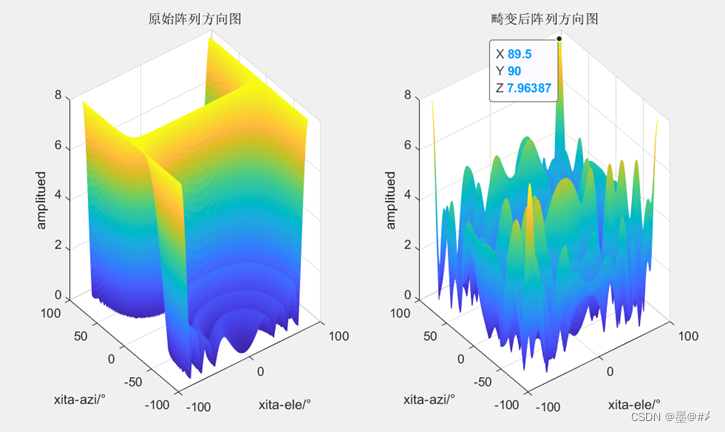
图3.13 Y方向畸变前后阵列波束图对比(1)

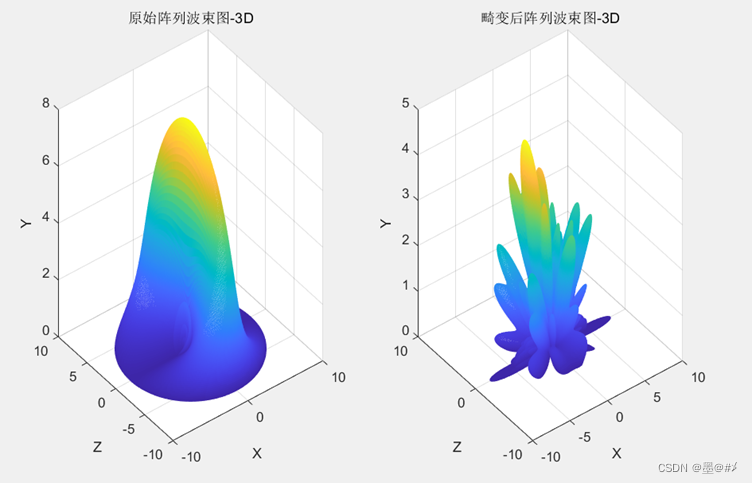
图3.14 Y方向畸变前后阵列波束图对比(2)

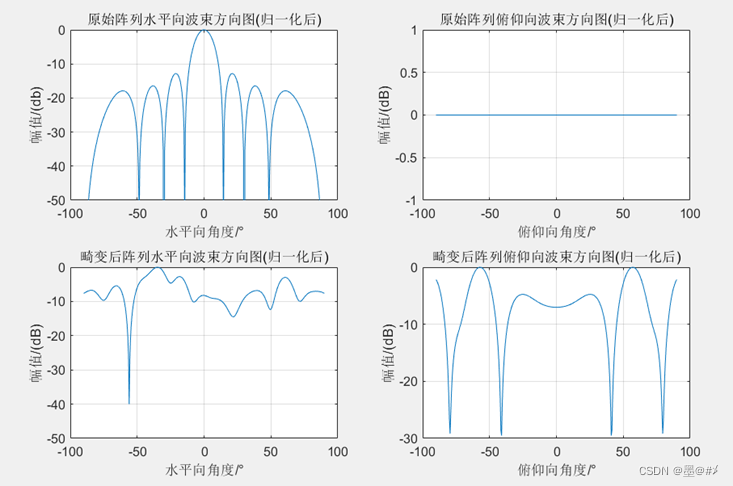
图3.15 Y方向畸变前后阵列波束图对比(3)

从前面几幅图的结果来看，Y方向的畸变对阵列波束方向图的影响最大！此时波束方向变得毫无规律可循。不过这也是符合预期的：因为前文中所分析的ddy的加入而引起的相位改变，会导致各阵元之间的相位关系完全不相关。

3.4 在三个维度同时发生畸变

畸变前后的阵列位置和波束方向图的仿真结果如下：

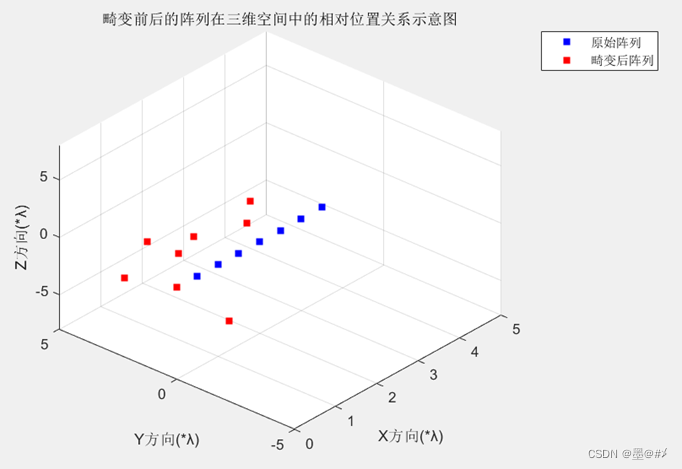
图3.16 三个方向同时畸变前后阵列位置关系图(1)

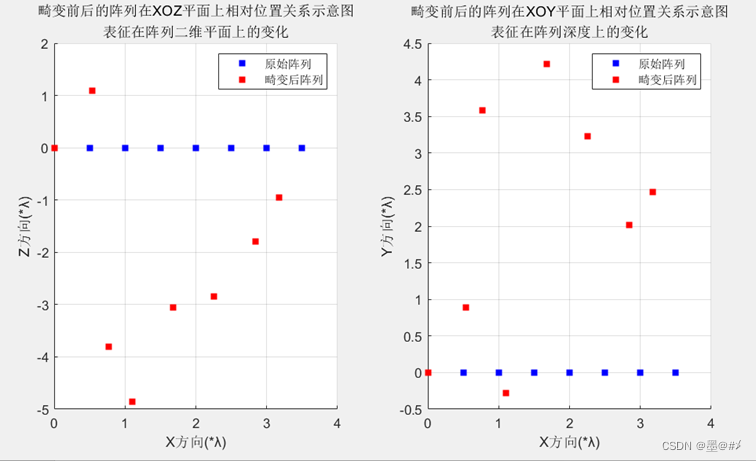
图3.17 三个方向同时畸变前后阵列位置关系图(2)

图3.18 三个方向同时畸变前后阵列波束图对比(1)

图3.19 三个方向同时畸变前后阵列波束图对比(2)

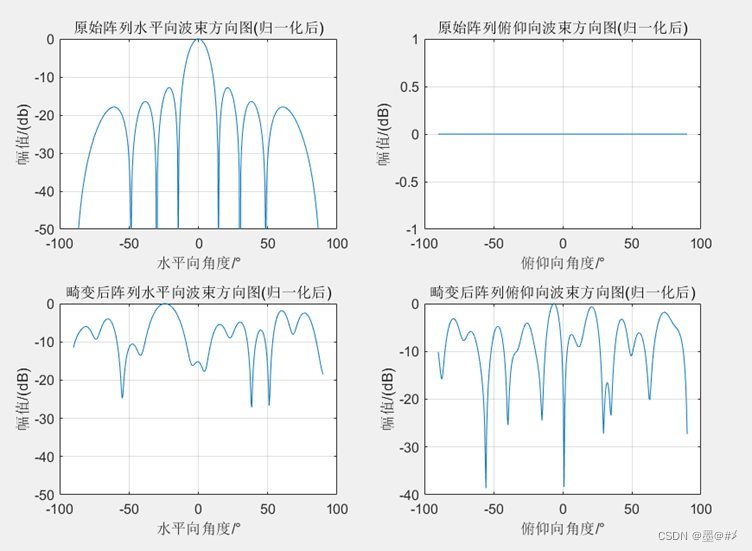
图3.20 三个方向同时畸变前后阵列波束图对比(3)

结论就是：完全乱了。

3.5 本章小结

本章在前文第1、2章的基础上，对一维线阵的畸变进行了仿真研究，具体地，本章分别给出了只在x方向畸变、只在y方向畸变、只在z方向畸变以及在三个维度(自由度)同时畸变四种情况下阵列畸变的前后排布对比和波束方向图对比。仿真的结果验证了前述理论的正确性，同时可以知道：阵列在Y方向(深度方向，当然，这与我们所预设的坐标系有关)的畸变影响最大。

其它的如任意两个维度的畸变极其波束方向图的效果、或者只对阵列中的其中某几个阵元进行畸变的结果这里就不给出了。读者可以基于提供的代码自行探讨(很简单，我给每个维度是否变化设置了开关，打开或者关闭即可，此外，在每个维度的变化幅度和方法，读者简单修改代码即可实现)。

四、柔性面阵波束方向图仿真结果与探讨

本章中仿真的基本参数列表如下：

表3.1 柔性阵列波束方向图仿真参数列表

参数	值
阵元个数	8*8
阵列类型	相邻阵元间隔0.5个波长的均匀面阵
载波频率	77GHz
X方向畸变范围	±0.25*λ(为了保证相邻阵元的位置不会“互换”)
Z方向畸变范围	±0.25*λ
Y方向畸变范围	±2.5*λ
畸变方法	每个阵元的畸变相对独立，在各个方向的畸变范围内随机产生畸变。
预设各阵元幅值	1
预设各阵元初始相位	0 【我在代码中也提供了不同角度下初始相位的设置方法，读者只需更改角度，即可计算得到特定角度下各阵元的初始相位值】

4.1 只在Y方向发生畸变

本节选取其中一个方向做畸变，畸变前后的阵列排布和波束图如下：

图4.1 只在Y方向发生畸变-畸变前后阵列位置关系图（1）

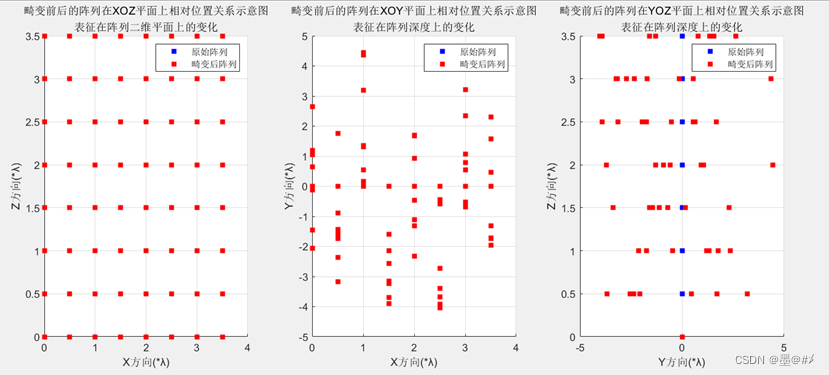
图4.2 只在Y方向发生畸变-畸变前后阵列位置关系图（2）

图4.3 只在Y方向畸变-畸变前后阵列波束图对比(1)

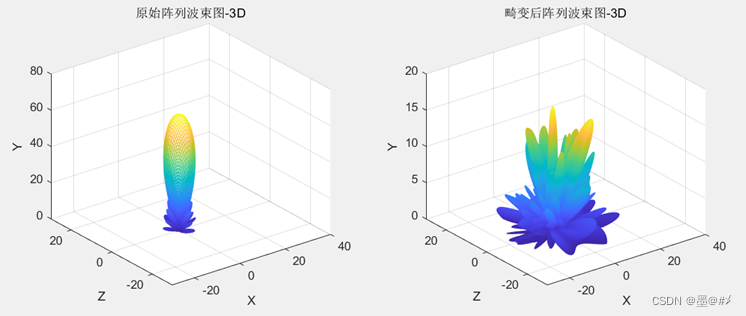
图4.4 只在Y方向畸变-畸变前后阵列波束图对比(2)

图4.5 只在Y方向畸变-畸变前后阵列波束图对比(3)

在本文所构建的坐标系中，Y方向对应为垂直阵列平面方向。可以看到原始阵列为长宽度相等的均匀面阵，所以其波束方向图在水平和俯仰两个方向是相同的，仿真结果符合预期。Y方向的畸变对于阵列的影响是最大的，所以可以看到畸变后的阵列波束方向图已经完全乱了。

在别的方向的畸变及其影响读者可以基于后文提供的代码进行探讨。

4.2 只在XOZ平面发生畸变

本节选取两个方向做畸变，畸变前后的阵列排布和波束方向图如下：

图4.6 在XOZ平面发生畸变-畸变前后阵列位置关系图（1）

图4.7 在XOZ平面发生畸变-畸变前后阵列位置关系图（2）

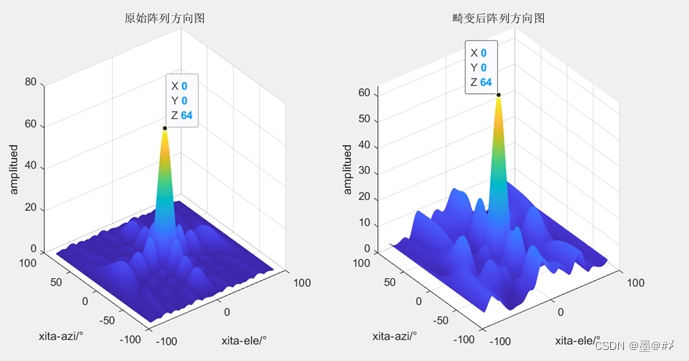
图4.8 在XOZ平面发生畸变-畸变前后阵列波束图对比(1)

图4.9 在XOZ平面发生畸变-畸变前后阵列波束图对比(2)

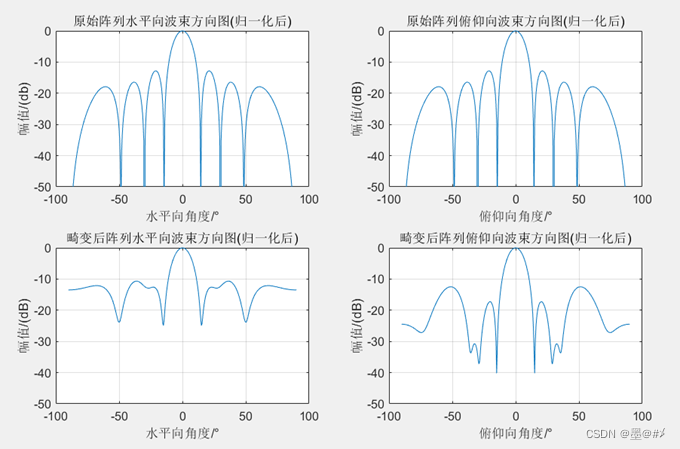
图4.10 在XOZ平面发生畸变-畸变前后阵列波束图对比(3)

从上面几幅图的结果来看，二维面阵在其所在平面发生的畸变会导致旁瓣的提高，但是似乎不会影响主瓣的方向。

在别的平面的畸变及其影响读者可以基于后文提供的代码进行探讨。

4.3 在三个维度同时发生畸变

畸变前后的阵列排布以及波束方向图的仿真结果如下：

图4.11 在三个维度同时发生畸变-畸变前后阵列位置关系图（1）

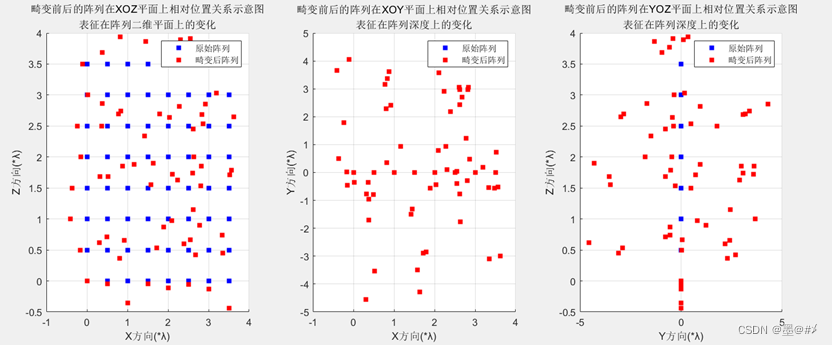
图4.12 在三个维度同时发生畸变-畸变前后阵列位置关系图（2）

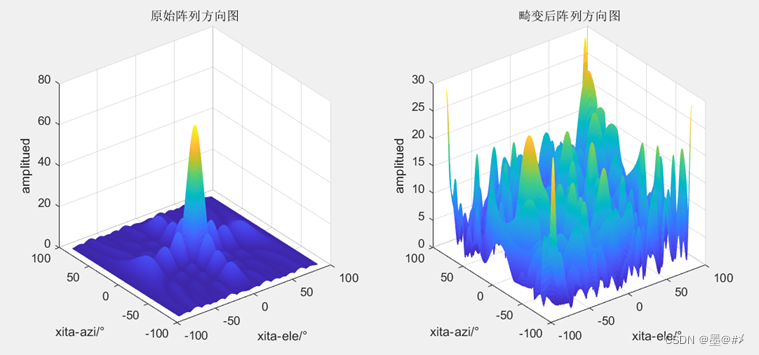
图4.13 在三个维度同时发生畸变-畸变前后阵列波束图对比(1)

图4.14 在三个维度同时发生畸变-畸变前后阵列波束图对比(2)

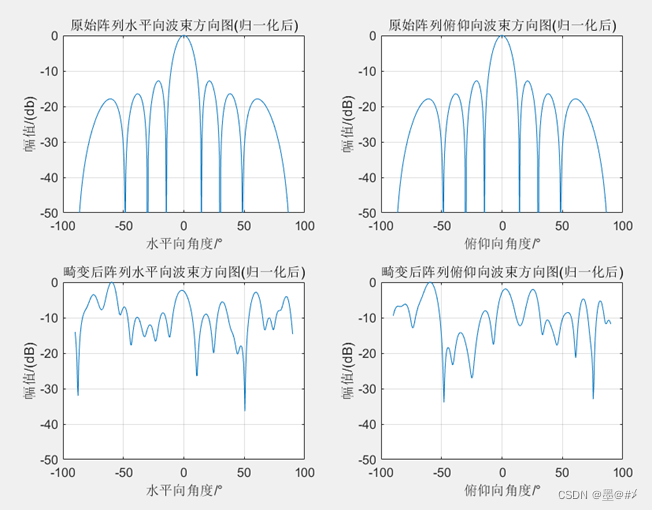
图4.15 在三个维度同时发生畸变-畸变前后阵列波束图对比(3)

从上面几幅图的结果可知，全乱了。

4.4 本章小结

本章在前文第1、2章的基础上，对二维面阵的畸变进行了仿真研究，具体地，本章分别给出了只在Y方向畸变、在XOZ平面畸变以及在三个维度(自由度)同时畸变三种情况下阵列畸变的前后排布对比和波束方向图对比。仿真的结果验证了前述理论的正确性，同时可以知道：阵列在Y方向的畸变影响最大。

五、柔性阵列稳健波束形成的方法思考

从上面两章的仿真结果可知，阵列畸变对于阵列方向图的影响可能是巨大的(特别是深度方向的影响)。在发射端：如果不对相位做补偿，要么旁瓣会很高，要么直接不知道主波束指向什么位置去了，这会极大地影响测量（比如所感兴趣区域的目标回波能量会极大衰弱）。同理，对于接收端：已经无法从各阵元的回波中获取可信的相位信息，无法直接进行DOA估计。

那么，如何做相位补偿？相位的改变本质上是因为阵元位置的改变导致的，所以通过获得每个阵元的位置畸变量，来得到需要进行补偿的相位是一种最直接的解决思路：比如可以在每个阵元所在的位置配置一个位姿传感器来实时获取位置畸变。或者，通过一些信号/数据处理的手段来推断出位置畸变[4][5]等。

稳健波束形成我现阶段的理解还不多，希望以后有机会深入研究并写写相关的博文(这也是为什么本博文的题目后面有序号(1)的原因)。

六、总结

本文探讨柔性阵列在位置畸变下的波束方向图问题。首先对柔性阵列、波束形成的概念进行了简要说明，并结合之前的积累[1]给出了一个三维阵列下阵列因子的通用表达式，在此基础上，分别基于线阵、面阵进行了仿真实践，探讨了在不同维度下位置畸变的影响。最后在第五章，简要探讨了如何对位置畸变后的阵列进行处理以消除/减弱畸变的影响。本章的内容主要旨在搭建一个阵列畸变研究的基本框架和基础，以期对后续更深入的研究有所帮助。