KNN的基本概念:
KNN(K-Nearest Neighbor)就是k个最近的邻居的意思,即每个样本都可以用它最接近的k个邻居来代表。KNN常用来处理分类问题,但也可以用来处理回归问题。
核心思想是如果一个样本在特征空间中的k个最相邻的样本中的大多数属于某一个类别,则该样本也属于这个类别,并具有这个类别上样本的特性。
相似度的衡量标准一般为距离,即距离越近相似度越高,距离越远相似度越小。
KNN算法三要素:
K值的选取
距离度量的方式
分类决策规则
K值的选择:
对于K值的选择,没有一个固定的经验(超参数)。选择较小的K值,就相当于用较小的邻域中的训练实例进行预测,训练误差会减小,容易发生过拟合,选择较大的K值,就相当于用较大邻域中的训练实例进行预测,其优点是可以减少泛华误差,缺点是训练误差会增大。K值一般根据样本的分布,选择较小的值,通常通过交叉验证选择一个合适的K值。
距离度量的方式:
欧氏距离(Euclidean Distance):这是最常用且直观的距离度量方法,它表示多维空间中两点之间的直线距离。在KNN中,欧氏距离通常用于连续数据的相似度计算。
曼哈顿距离(Manhattan Distance):也称为城市街区距离,它是沿着坐标轴测量的距离,适合用于城市地图中的距离计算,其中不能直接穿过建筑物或街区。在KNN中,当处理离散数据或者特征之间相互独立时,曼哈顿距离可能会被使用。
切比雪夫距离(Chebyshev Distance):在无限维的多项式空间中,切比雪夫距离是最大值范数,即各坐标数值差的最大值。这种距离度量方式适用于当一个属性对结果的影响非常显著时的场景。
除了上述三种,还有明可夫斯基距离(Minkowski Distance)、余弦相似度(Cosine Similarity)等其他距离度量方式
KNN的优缺点:
KNN算法的优点:
理论成熟,思想简单,
既可以用来做分类也可以用来做回归;
可用于非线性分类; 对数据没有假设,准确度高,对噪声不敏感。
KNN算法的缺点:
计算量大;
样本不平衡问题 (即有些类别的样本数量很多,而其它样本的数量很少);
需要大量的内存。
KNN算法内参数:
n_neighbors:K值
即K值,邻近点的个数
weights:权重
{‘uniform’, ‘distance’}, callable or None, default=’uniform’
unifrom:表示权重相同,即只按照邻近点的多少判断其属于哪一类。
distance:表示权重于距离相关,距离近的点权重高,可能按照最近点来判断属于哪一类点
algorithm:计算临近点所用算法
brute:暴力法,即计算出所有点的距离,选择最近的几个点。
kd树:具体原理较为复杂,推荐大家
https://www.cnblogs.com/ssyfj/p/13053055.html 这里kd树的原理解释的非常清楚
ball_tree:kd树一般用于20维以下,而kd树一旦超过20维,效果会不尽人意,因此ball_tree就是为了解决高维问题而提出的,具体原理大家可以去网上学习一下原理。
p:默认值为2,表示Minkowski度量的幂参数
当p=1时,等效于使用曼哈顿距离(l1),当p=2时,等效于使用欧几里得距离(l2)。对于任意p,使用Minkowski距离(l_p)。此参数应为正数。
metric:距离的计算方式
比如:欧氏距离,曼哈顿距离等,默认为:minkowski。
代码实现:
from sklearn.neighbors import KNeighborsClassifier,KNeighborsRegressor #C是处理分类,R是处理回归
from sklearn.datasets import load_wine
wine = load_wine()
X = wine.data
y = wine.target
knn = KNeighborsClassifier(n_neighbors=5)
from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.3,random_state=42)
knn.fit(X_train,y_train)
print(knn.score(X_test,y_test))
# 结果为:0.7407407407407407
# 可以看到结果并不是很好,所以我们进行优化,调参
from sklearn.neighbors import KNeighborsClassifier,KNeighborsRegressor #C是处理分类,R是处理回归
from sklearn.datasets import load_wine
wine = load_wine()
X = wine.data
y = wine.target
knn = KNeighborsClassifier(n_neighbors=10)
from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.3,random_state=42)
# print(knn.score(X_test,y_test))
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import confusion_matrix
ss = StandardScaler()
ss.fit(X_train)
X_train = ss.transform(X_train)
X_test = ss.transform(X_test)
knn.fit(X_train,y_train)
cm = confusion_matrix(y_true=y_test,y_pred=knn.predict(X_test))
import seaborn as sns
import matplotlib.pyplot as plt
sns.heatmap(cm,annot=True,cmap="Blues")
print(knn.score(X_test,y_test))
plt.show()
# 结果:0.9629629629629629
# 可以看出,调参后准确率有明显改变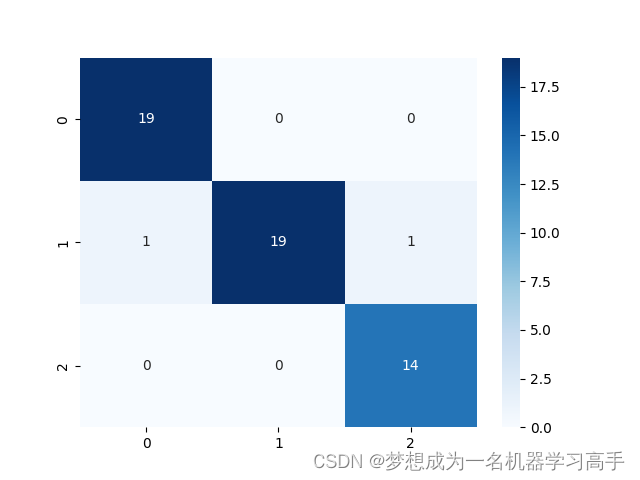
上述是处理分类问题: 对于回归问题我们怎么做呢
import numpy as np
from sklearn.neighbors import KNeighborsRegressor
from sklearn.model_selection import train_test_split
# 创建数据集
X = np.array([[1, 2], [3, 4], [5, 6], [7, 8], [9, 10]])
y = np.array([2, 4, 6, 8, 10])
# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# 创建KNN回归模型
knn = KNeighborsRegressor(n_neighbors=3)
# 训练模型
knn.fit(X_train, y_train)
# 预测
y_pred = knn.predict(X_test)
# 将预测值打印出来
print(y_pred)