目录

思路 

代码思路

代码

推荐 

---

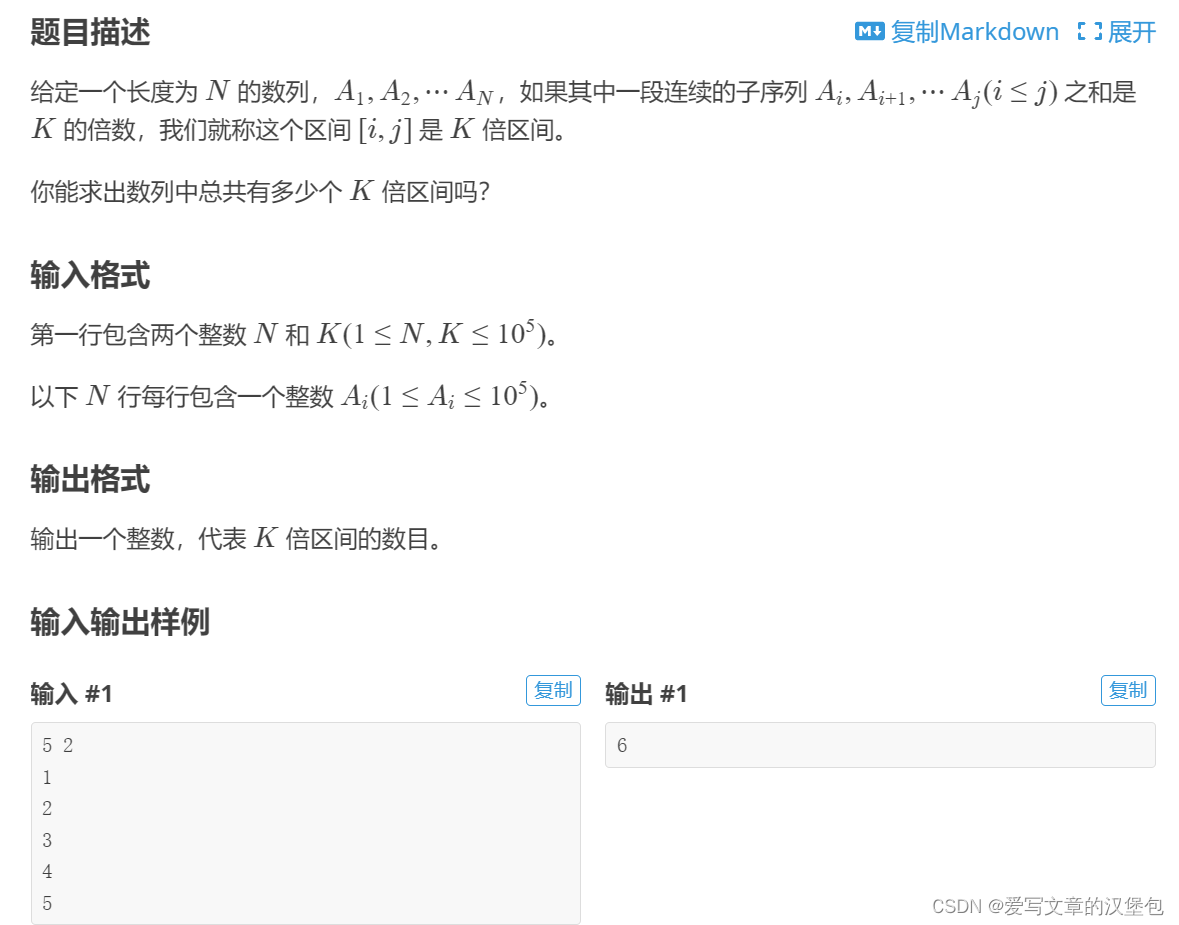
P8649 [蓝桥杯 2017 省 B] k 倍区间

思路 

额嗯，这道题我刚上来是想到了前缀和，但是还要判断每个子序列，我就两层for嵌套，暴力解了题。就是我知道暴力肯定过不了但是写不出来其他的[留下了苦涩的眼泪hh]

这道题用到了数学知识：同余定理：给定一个正整数m，如果两个整数a和b满足a-b能够被m整除，即 (a-b)/m得到一个整数，那么就称整数a与b对模m同余，记作a≡b (mod m)。

也就是如果两个数对k取余，且余数相同，那么这两个数相减再对k取余，就会得到余数是0，也就是整除了。

那么对应到我们这道题里，我们按正常方法计算出前缀和，在对每一个前缀和的值进行对k取余，用一个数组来存储对应余数出现的次数，在这些具有相同余数的数中，任取两个数进行相减都会得到一段满足条件的K倍区间。(这里注意理解一下 数与区间 的转化，因为我们进行相减的数是某个前缀和，也就是某段区间的和，那么既然是两个区间的相减，得到的也就是一段符合条件的区间)

这个任取的过程用数学知识可以表示为Cx(下标)2(上标)

代码思路

① 

这道题我们甚至可以不开前缀和数组，因为我们计算同余数字的个数的话，其实只对最初求出的前缀和进行取模操作，而不需要对某两个前缀和进行处理，也就是说，其实这个前缀和数组我们也只是使用到了一次而已，因此，在这里不设前缀和数组和前缀和算法中原数组可以不设的原因是一样的，我们可以直接设一个变量来表示每个数与前一个数相加的和。

②

为了避免每次输入进来的数据太大，我们甚至可以直接在把这个数加到前缀和中的时候就直接加该数对k取模之后的余数的值，因为我们最后也是要对每个前缀和取模的嘛。

(我想表达的是这样：)

for(int i=1;i<=n;i++)
	{
		int x;
		cin>>x;
		sum+=x%k;//直接用sum一个变量表示每次更新的前缀和，每次更新即可。
		s[sum%k]++;
		sum%=k;
	}

 ③

说一下Cx(下标)2(上标)应该怎样计算，看着好像无从下手(我无从下手doge)，其实很简单，就把它按数学里学的那样展开，就得到=(x*(x-1))/2就可以啦

另外有一点，我们最终进行计算的主要是围绕每个相同余数的数的个数，也就是s数组，要考虑到当余数是0的时候，其实相较于我们的通式(x*(x-1))/2是要多1的，可以通过举例来得到。因此对于s数组0所对应的初始值应该为1.

具体的解释可以看这个博主的题解(我也是主要看这个博主看明白哒)

【题解】P8649 题解

代码

#include<iostream>
#define int long long
using namespace std;
const int N=1e5+10;
int n,k;
int s[N];//用来存储同一个余数的个数
signed main()
{
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);
	cin>>n>>k;
	int sum=0;
	s[0]=1;
	for(int i=1;i<=n;i++)
	{
		int x;
		cin>>x;
		sum+=x%k;
		s[sum%k]++;
		sum%=k;
	}
	int cnt=0;
	for(int i=0;i<k;i++)//遍历所有可能的相同余数
	{
		cnt+=(s[i]*(s[i]-1))/2;
	}
	cout<<cnt;
	return 0;
 } 

关于代码中一些书写上的 

ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);

这三行是提速的。

#define int long long
...
signed main()

这里是为了避免忘记开long long导致丢分写的，也就是表示我们用int这个外号来表示long long 的新名字，这样写的话下面主函数int main() 记得前面的int变成 signed。

如果想了解更清晰的，可以看这个up猪的完整视频，我是蒟蒻hhh

【[蓝桥杯]避免常见坑点（输入输出问题、数据溢出问题等）】

这个就看个人习惯了. 

推荐 

这个博主简化了 Cx(下标)2(上标) 的计算过程，代码更简洁清晰，感兴趣可以看一下

17行代码解决

或许可以帮助大家理解 

---

呜呜感觉好菜呀🥀🥀🥀

有问题欢迎指出，一起加油！！