学习率调整得当将有助于算法快速收敛和获取全局最优,以获得更好的性能。本文对学习率调度器进行示例介绍。
- 学习率调整的意义
- 基础示例
- 无学习率调整方法
- 学习率调整方法一
- 多因子调度器
- 余弦调度器
- 结论
学习率调整的意义
首先,学习率的大小很重要。如果它太大,优化就会发散;如果它太小,训练就会需要过长时间,或者我们最终只能得到次优的结果(陷入局部最优)。我们之前看到问题的条件数很重要。直观地说,这是最不敏感与最敏感方向的变化量的比率。
其次,衰减速率同样很重要。如果学习率持续过高,我们可能最终会在最小值附近弹跳,从而无法达到最优解。 简而言之,我们希望速率衰减,但要比慢,这样能成为解决凸问题的不错选择。
另一个同样重要的方面是初始化。这既涉及参数最初的设置方式,又关系到它们最初的演变方式。这被戏称为预热(warmup),即我们最初开始向着解决方案迈进的速度有多快。一开始的大步可能没有好处,特别是因为最初的参数集是随机的。最初的更新方向可能也是毫无意义的。
鉴于管理学习率需要很多细节,因此大多数深度学习框架都有自动应对这个问题的工具。本文将梳理不同的调度策略对准确性的影响,并展示如何通过学习率调度器(learning rate scheduler)来有效管理。
基础示例
我们从一个简单的问题开始,这个问题可以轻松计算,但足以说明要义。 为此,我们选择了一个稍微现代化的LeNet版本(激活函数使用relu而不是sigmoid,汇聚层使用最大汇聚层而不是平均汇聚层),并应用于Fashion-MNIST数据集。 此外,我们混合网络以提高性能。
无学习率调整方法
import math
import torch
from torch import nn
from torch.optim import lr_scheduler, SGD
from torchvision import datasets, transforms
from torch.utils.data import DataLoader
from torchvision.utils import make_grid
import matplotlib.pyplot as plt
def load_data_fashion_mnist(batch_size):
# 定义数据预处理
transform = transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.5,), (0.5,))
])
# 加载训练集和测试集
train_dataset = datasets.FashionMNIST(root='./data', train=True, download=True, transform=transform)
test_dataset = datasets.FashionMNIST(root='./data', train=False, download=True, transform=transform)
# 创建数据加载器
train_loader = DataLoader(train_dataset, batch_size=batch_size, shuffle=True)
test_loader = DataLoader(test_dataset, batch_size=batch_size, shuffle=False)
return train_loader, test_loader
def net_fn():
model = nn.Sequential(
nn.Conv2d(1, 6, kernel_size=5, padding=2), nn.ReLU(),
nn.MaxPool2d(kernel_size=2, stride=2),
nn.Conv2d(6, 16, kernel_size=5), nn.ReLU(),
nn.MaxPool2d(kernel_size=2, stride=2),
nn.Flatten(),
nn.Linear(16 * 5 * 5, 120), nn.ReLU(),
nn.Linear(120, 84), nn.ReLU(),
nn.Linear(84, 10))
return model
def train(net, train_loader, test_loader, num_epochs, loss, optimizer, device, scheduler=None):
net.to(device)
running_loss = 0.0
train_losses = []
test_losses = []
test_accuracies = []
for epoch in range(num_epochs):
for i, (inputs, labels) in enumerate(train_loader):
inputs, labels = inputs.to(device), labels.to(device)
# Zero the parameter gradients
optimizer.zero_grad()
# Forward pass
outputs = net(inputs)
loss_value = loss(outputs, labels)
# Backward and optimize
loss_value.backward()
optimizer.step()
# Print statistics
running_loss += loss_value.item()
# if i % 200 == 199: # print every 200 mini-batches
# print(f'[{epoch + 1}, {i + 1}] loss: {running_loss / 200}')
# running_loss = 0.0
train_losses.append(running_loss / len(train_loader))
# Evaluate the model on the test dataset
test_loss, test_acc = evaluate(net, test_loader, device)
test_losses.append(test_loss)
test_accuracies.append(test_acc)
print(f'Epoch {epoch+1}, Train Loss: {train_losses[-1]:.4f}, Test Loss: {test_losses[-1]:.4f}, Test Acc: {test_accuracies[-1]:.2f}')
if scheduler:
if scheduler.__module__ == lr_scheduler.__name__:
scheduler.step()
else:
for param_group in optimizer.param_groups:
param_group['lr'] = scheduler(epoch)
plt.figure(figsize=(10, 6))
plt.plot(range(1, num_epochs + 1), train_losses, label='Training Loss')
plt.plot(range(1, num_epochs + 1), test_losses, label='Test Loss')
plt.plot(range(1, num_epochs + 1), test_accuracies, label='Test Accuracy')
plt.title('Training, Test Losses and Test Accuracy')
plt.xlabel('Epoch')
plt.ylabel('Loss / Accuracy')
plt.legend()
plt.grid(True)
plt.savefig("1.jpg")
plt.show()
def evaluate(model, data_loader, device):
model.eval()
test_loss = 0
correct = 0
with torch.no_grad():
for inputs, labels in data_loader:
inputs, labels = inputs.to(device), labels.to(device)
outputs = model(inputs)
test_loss += nn.CrossEntropyLoss(reduction='sum')(outputs, labels).item()
_, predicted = torch.max(outputs.data, 1)
correct += (predicted == labels).sum().item()
test_loss /= len(data_loader.dataset)
accuracy = correct / len(data_loader.dataset)
#accuracy = 100. * correct / len(data_loader.dataset)
return test_loss, accuracy
# Device configuration
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
# Define the model
model = net_fn()
# Define the loss function
loss = nn.CrossEntropyLoss()
# Define the optimizer
lr=0.3
optimizer = SGD(model.parameters(), lr=lr)
# Load the dataset
batch_size=128
train_loader, test_loader=load_data_fashion_mnist(batch_size)
num_epochs=30
train(model, train_loader, test_loader, num_epochs, loss, optimizer, device)
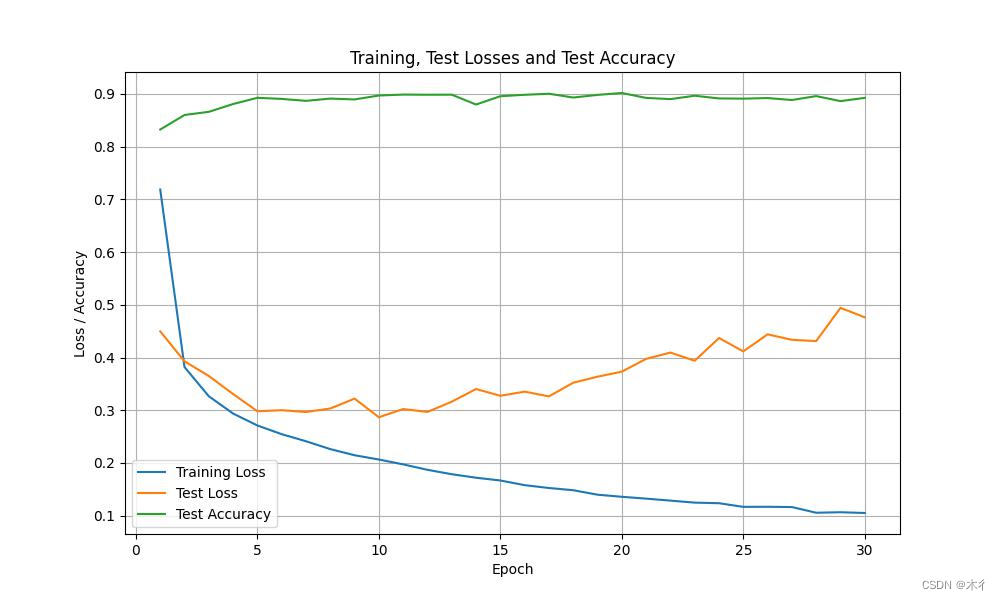
这里没有使用学习率调整策略。训练过程和结果如下图所示:
.
.
.
.
Epoch 23, Train Loss: 0.1247, Test Loss: 0.3939, Test Acc: 0.90
Epoch 24, Train Loss: 0.1236, Test Loss: 0.4370, Test Acc: 0.89
Epoch 25, Train Loss: 0.1167, Test Loss: 0.4117, Test Acc: 0.89
Epoch 26, Train Loss: 0.1169, Test Loss: 0.4440, Test Acc: 0.89
Epoch 27, Train Loss: 0.1163, Test Loss: 0.4336, Test Acc: 0.89
Epoch 28, Train Loss: 0.1055, Test Loss: 0.4312, Test Acc: 0.90
Epoch 29, Train Loss: 0.1065, Test Loss: 0.4942, Test Acc: 0.89
Epoch 30, Train Loss: 0.1051, Test Loss: 0.4763, Test Acc: 0.89
学习率调整方法一
设置在每个迭代轮数(甚至在每个小批量)之后向下调整学习率。 例如,以动态的方式来响应优化的进展情况。
在代码最后添加SquareRootScheduler类,并更新train()函数参数,其它内容不变。
class SquareRootScheduler:
def __init__(self, lr=0.1):
self.lr = lr
def __call__(self, num_update):
return self.lr * pow(num_update + 1.0, -0.5)
scheduler = SquareRootScheduler(lr=0.1)
train(model, train_loader, test_loader, num_epochs, loss, optimizer, device,scheduler)
运行代码,可得相应参数值和变化过程,如下所示。
Epoch 23, Train Loss: 0.1823, Test Loss: 0.2811, Test Acc: 0.90
Epoch 24, Train Loss: 0.1801, Test Loss: 0.2800, Test Acc: 0.90
Epoch 25, Train Loss: 0.1767, Test Loss: 0.2819, Test Acc: 0.90
Epoch 26, Train Loss: 0.1747, Test Loss: 0.2800, Test Acc: 0.91
Epoch 27, Train Loss: 0.1720, Test Loss: 0.2818, Test Acc: 0.90
Epoch 28, Train Loss: 0.1689, Test Loss: 0.2856, Test Acc: 0.90
Epoch 29, Train Loss: 0.1669, Test Loss: 0.2907, Test Acc: 0.90
Epoch 30, Train Loss: 0.1641, Test Loss: 0.2813, Test Acc: 0.90
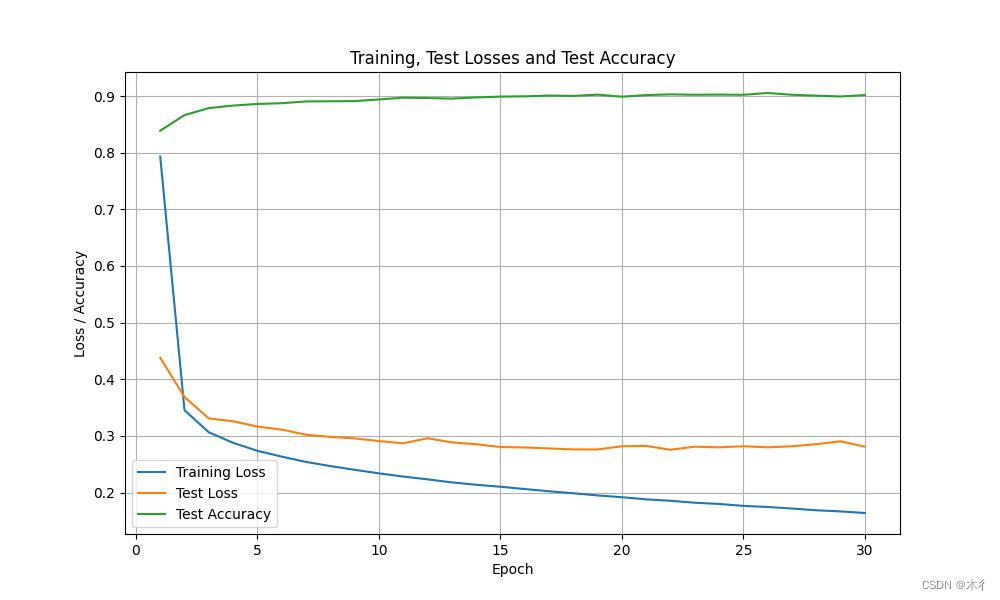
我们可以看出曲线比没有策略时平滑了很多,效果有所提升。
多因子调度器
多因子调度器。

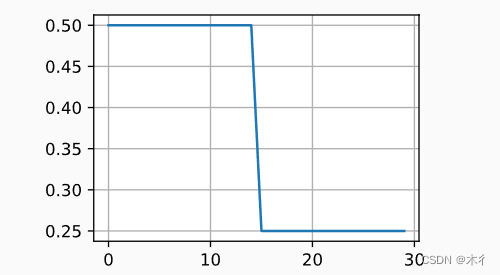
代码部分修改:
scheduler =lr_scheduler.MultiStepLR(optimizer, milestones=[15, 30], gamma=0.5)
运行结果为:
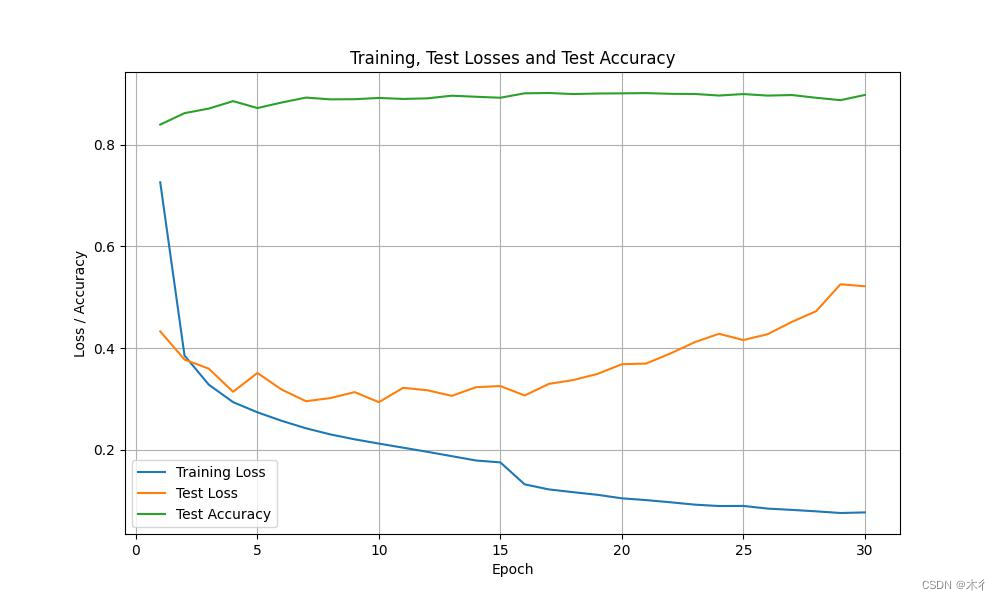
可见效果不理想,出现过拟合现象。
余弦调度器
余弦调度器是 (Loshchilov and Hutter, 2016)提出的一种启发式算法。 它所依据的观点是:我们可能不想在一开始就太大地降低学习率,而且可能希望最终能用非常小的学习率来“改进”解决方案。 这产生了一个类似于余弦的调度,函数形式如下所示,学习率的值在
之间。

代码中添加CosineScheduler类和修改scheduler。
class CosineScheduler:
def __init__(self, max_update, base_lr=0.01, final_lr=0,
warmup_steps=0, warmup_begin_lr=0):
self.base_lr_orig = base_lr
self.max_update = max_update
self.final_lr = final_lr
self.warmup_steps = warmup_steps
self.warmup_begin_lr = warmup_begin_lr
self.max_steps = self.max_update - self.warmup_steps
def get_warmup_lr(self, epoch):
increase = (self.base_lr_orig - self.warmup_begin_lr) \
* float(epoch) / float(self.warmup_steps)
return self.warmup_begin_lr + increase
def __call__(self, epoch):
if epoch < self.warmup_steps:
return self.get_warmup_lr(epoch)
if epoch <= self.max_update:
self.base_lr = self.final_lr + (
self.base_lr_orig - self.final_lr) * (1 + math.cos(
math.pi * (epoch - self.warmup_steps) / self.max_steps)) / 2
return self.base_lr
#scheduler = SquareRootScheduler(lr=0.1)
#scheduler =lr_scheduler.MultiStepLR(optimizer, milestones=[15, 30], gamma=0.5)
scheduler = CosineScheduler(max_update=20, base_lr=0.3, final_lr=0.01)
train(model, train_loader, test_loader, num_epochs, loss, optimizer, device,scheduler)
运行结果如下:
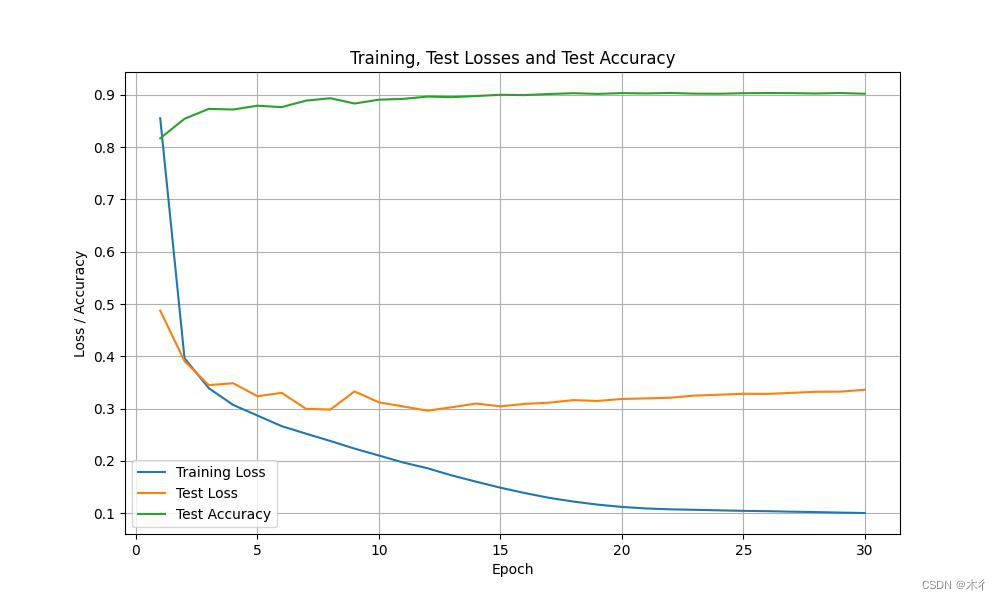
过拟合现象消失,效果提升。
结论
在开发时应根据自己需要,选择合适的学习率调整策略。优化在深度学习中有多种用途。对于同样的训练误差而言,选择不同的优化算法和学习率调度,除了最大限度地减少训练时间,可以导致测试集上不同的泛化和过拟合量。
注:部分内容摘选子书籍《动手学深度学习》