【题解】—— 每日一道题目栏
上接:【题解】—— LeetCode一周小结11
18.区域和检索 - 数组不可变
题目链接:303. 区域和检索 - 数组不可变
1.计算索引 left 和 right (包含 left 和 right)之间的 nums 元素的 和 ,其中 left <= right
实现 NumArray 类:
- NumArray(int[] nums) 使用数组 nums 初始化对象
- int sumRange(int i, int j) 返回数组 nums 中索引 left 和 right 之间的元素的 总和 ,包含 left 和 right 两点(也就是 nums[left] + nums[left + 1] + … + nums[right] )
示例 1:
输入:
[“NumArray”, “sumRange”, “sumRange”, “sumRange”]
[[[-2, 0, 3, -5, 2, -1]], [0, 2], [2, 5], [0, 5]]
输出:
[null, 1, -1, -3]
解释:
NumArray numArray = new NumArray([-2, 0, 3, -5, 2, -1]);
numArray.sumRange(0, 2); // return 1 ((-2) + 0 + 3)
numArray.sumRange(2, 5); // return -1 (3 + (-5) + 2 + (-1))
numArray.sumRange(0, 5); // return -3 ((-2) + 0 + 3 + (-5) + 2 + (-1))
提示:
1 <= nums.length <= 104
-105 <= nums[i] <= 105
0 <= i <= j < nums.length
最多调用 104 次 sumRange 方法
题解:
方法:前缀和
设计一个前缀和数组(s),用于存储给定数组 nums 的前缀和。
在初始化 NumArray 对象时,首先创建前缀和数组,并计算出给定数组 nums 的每个位置的前缀和,存储在 s 数组中。
在求解 sumRange 时,只需利用前缀和数组 s,即可在 O(1) 时间内求出指定区间 [left, right] 的和,即 s[right + 1] - s[left]。
class NumArray {
private int[] s; // 前缀和数组
// 构造函数,初始化前缀和数组
public NumArray(int[] nums) {
s = new int[nums.length + 1];
for (int i = 0; i < nums.length; i++) {
s[i + 1] = s[i] + nums[i]; // 计算前缀和
}
}
// 求解给定区间[left, right]的和
public int sumRange(int left, int right) {
return s[right + 1] - s[left]; // 返回区间和
}
}
/**
* Your NumArray object will be instantiated and called as such:
* NumArray obj = new NumArray(nums);
* int param_1 = obj.sumRange(left,right);
*/
扩展
- 如何计算数组元素到某个数的距离之和?见 2602. 使数组元素全部相等的最少操作次数,题解
- 如何计算元素和等于 k 的子数组个数?见 560. 和为 K 的子数组
- 把 nums改成二维矩阵,如何计算子矩阵的元素和?见 304. 二维区域和检索 - 矩阵不可变,图解
- 如果可以修改 nums的元素值呢?见 307. 区域和检索 - 数组可修改,题解
- 对于 53. 最大子数组和,除了 DP 做法外,还可以用 前缀和 解决。这一做法可以扩展到子数组长度有下限/上限,子数组元素和有上限等。
题单:前缀和
560. 和为 K 的子数组
930. 和相同的二元子数组
1524. 和为奇数的子数组数目
974. 和可被 K 整除的子数组
523. 连续的子数组和
3026. 最大好子数组和
525. 连续数组
面试题 17.05. 字母与数字
1124. 表现良好的最长时间段
2488. 统计中位数为 K 的子数组
1590. 使数组和能被 P 整除
2949. 统计美丽子字符串 II
1983. 范围和相等的最宽索引对
2489. 固定比率的子字符串数
2955. 同端子串的数量
题单:异或前缀和
1310. 子数组异或查询
1177. 构建回文串检测
1371. 每个元音包含偶数次的最长子字符串
1542. 找出最长的超赞子字符串
1915. 最美子字符串的数目
2791. 树中可以形成回文的路径数
19.好子数组的最大分数
题目链接:1793. 好子数组的最大分数
给你一个整数数组 nums (下标从 0 开始)和一个整数 k 。
一个子数组 (i, j) 的 分数 定义为 min(nums[i], nums[i+1], …, nums[j]) * (j - i + 1) 。一个 好 子数组的两个端点下标需要满足 i <= k <= j 。
请你返回 好 子数组的最大可能 分数 。
示例 1:
输入:nums = [1,4,3,7,4,5], k = 3
输出:15
解释:最优子数组的左右端点下标是 (1, 5) ,分数为 min(4,3,7,4,5) * (5-1+1) = 3 * 5 = 15 。
示例 2:
输入:nums = [5,5,4,5,4,1,1,1], k = 0
输出:20
解释:最优子数组的左右端点下标是 (0, 4) ,分数为 min(5,5,4,5,4) * (4-0+1) = 4 * 5 = 20 。
提示:
1 <= nums.length <= 105
1 <= nums[i] <= 2 * 104
0 <= k < nums.length
题解:
方法:单调栈
这个问题可以使用单调栈来解决。
首先,我们需要求出每个位置 i 左边第一个小于 nums[i] 的位置 left[i],以及右边第一个小于 nums[i] 的位置 right[i]。
这样,对于每个位置 i,我们可以计算以 nums[i] 作为高度的最大矩形面积,即 (right[i] - left[i] - 1) * nums[i]。
我们遍历所有位置 i,计算对应的最大面积,并返回最大值即可。
class Solution {
public int maximumScore(int[] nums, int k) {
int n = nums.length;
int[] left = new int[n];
Deque<Integer> st = new ArrayDeque<>();
// 计算每个位置 i 左边第一个小于 nums[i] 的位置 left[i]
for (int i = 0; i < n; i++) {
int x = nums[i];
while (!st.isEmpty() && x <= nums[st.peek()]) {
st.pop();
}
left[i] = st.isEmpty() ? -1 : st.peek();
st.push(i);
}
// 清空栈,准备计算右边第一个小于 nums[i] 的位置 right[i]
st.clear();
// 计算每个位置 i 右边第一个小于 nums[i] 的位置 right[i]
for (int i = n - 1; i >= 0; i--) {
int x = nums[i];
while (!st.isEmpty() && x <= nums[st.peek()]) {
st.pop();
}
right[i] = st.isEmpty() ? n : st.peek();
st.push(i);
}
// 计算最大矩形面积
int ans = 0;
for (int i = 0; i < n; i++) {
int h = nums[i];
int l = left[i];
int r = right[i];
if (l < k && k < r) { // 如果 k 位置在 [l, r] 之间
ans = Math.max(ans, h * (r - l - 1));
}
}
return ans;
}
}
方法:双指针
我们使用两个指针 i 和 j 来表示当前矩形的左右边界。
我们从位置 k 开始,向左右两个方向扩展,每次选择高度较小的边界向内移动,直到两个边界相遇或者超出数组边界。
在移动过程中,我们不断更新当前的最小高度 minH,并计算以当前最小高度为高的矩形的面积,更新答案。
最终返回最大面积。
class Solution {
public int maximumScore(int[] nums, int k) {
int n = nums.length;
int ans = nums[k]; // 初始化答案为 nums[k]
int minH = nums[k]; // 初始化当前最小高度为 nums[k]
int i = k, j = k; // 初始化两个指针为 k
// 循环 n-1 次
for (int t = 0; t < n - 1; t++) {
// 如果 j 边界到达数组右端或者 i 边界大于 0 且 i-1 位置高度大于 j+1 位置高度
if (j == n - 1 || (i > 0 && nums[i - 1] > nums[j + 1])) {
minH = Math.min(minH, nums[--i]); // 向左移动 i 指针
} else {
minH = Math.min(minH, nums[++j]); // 向右移动 j 指针
}
ans = Math.max(ans, minH * (j - i + 1)); // 计算以当前最小高度为高的矩形面积并更新答案
}
return ans;
}
}
20.数组元素的最小非零乘积
题目链接:1969. 数组元素的最小非零乘积
给你一个正整数 p 。你有一个下标从 1 开始的数组 nums ,这个数组包含范围 [1, 2p - 1] 内所有整数的二进制形式(两端都 包含)。你可以进行以下操作 任意 次:
- 从 nums 中选择两个元素 x 和 y 。
- 选择 x 中的一位与 y 对应位置的位交换。对应位置指的是两个整数 相同位置 的二进制位。
比方说,如果 x = 1101 且 y = 0011 ,交换右边数起第 2 位后,我们得到 x = 1111 和 y = 0001 。
请你算出进行以上操作 任意次 以后,nums 能得到的 最小非零 乘积。将乘积对 109 + 7 取余 后返回。
注意:答案应为取余 之前 的最小值。
示例 1:
输入:p = 1
输出:1
解释:nums = [1] 。
只有一个元素,所以乘积为该元素。
示例 2:
输入:p = 2
输出:6
解释:nums = [01, 10, 11] 。
所有交换要么使乘积变为 0 ,要么乘积与初始乘积相同。
所以,数组乘积 1 * 2 * 3 = 6 已经是最小值。
示例 3:
输入:p = 3
输出:1512
解释:nums = [001, 010, 011, 100, 101, 110, 111]
- 第一次操作中,我们交换第二个和第五个元素最左边的数位。
- 结果数组为 [001, 110, 011, 100, 001, 110, 111] 。
- 第二次操作中,我们交换第三个和第四个元素中间的数位。
- 结果数组为 [001, 110, 001, 110, 001, 110, 111] 。
数组乘积 1 * 6 * 1 * 6 * 1 * 6 * 7 = 1512 是最小乘积。
提示:
1 <= p <= 60
题解:
方法:贪心
首先,计算出 2^p - 1 的值,记为 k。然后,计算 k * (k - 1)^(p - 1) 的结果,并对结果取模。在计算过程中,使用快速幂算法来计算幂次方,以避免大数幂的过程中的性能问题。
注释:
- pow方法:快速幂算法,计算 x^p % MOD 的结果。
- minNonZeroProduct方法:根据贪心思路求解最小非零乘积的问题。首先计算出 k = 2^p - 1,然后计算 k * (k - 1)^(p - 1) 的结果,并对结果取模后返回。
public class Solution {
private static final int MOD = 1_000_000_007;
// 快速幂算法
private long pow(long x, int p) {
x %= MOD;
long res = 1;
while (p-- > 0) {
res = res * x % MOD;
x = x * x % MOD;
}
return res;
}
// 求解最小非零乘积的问题
public int minNonZeroProduct(int p) {
long k = (1L << p) - 1; // 计算 2^p - 1
return (int) (k % MOD * pow(k - 1, p - 1) % MOD); // 计算 k * (k - 1)^(p - 1) % MOD 的结果并返回
}
}
21.频率跟踪器
题目链接:2671. 频率跟踪器
请你设计并实现一个能够对其中的值进行跟踪的数据结构,并支持对频率相关查询进行应答。
实现 FrequencyTracker 类:
- FrequencyTracker():使用一个空数组初始化 FrequencyTracker 对象。
- void add(int number):添加一个 number 到数据结构中。
- void deleteOne(int number):从数据结构中删除一个 number 。数据结构 可能不包含 number ,在这种情况下不删除任何内容。
- bool hasFrequency(int frequency): 如果数据结构中存在出现 frequency 次的数字,则返回 true,否则返回 false。
示例 1:
输入
[“FrequencyTracker”, “add”, “add”, “hasFrequency”]
[[], [3], [3], [2]]
输出
[null, null, null, true]
解释
FrequencyTracker frequencyTracker = new FrequencyTracker();
frequencyTracker.add(3); // 数据结构现在包含 [3]
frequencyTracker.add(3); // 数据结构现在包含 [3, 3]
frequencyTracker.hasFrequency(2); // 返回 true ,因为 3 出现 2 次
示例 2:
输入
[“FrequencyTracker”, “add”, “deleteOne”, “hasFrequency”]
[[], [1], [1], [1]]
输出
[null, null, null, false]
解释
FrequencyTracker frequencyTracker = new FrequencyTracker();
frequencyTracker.add(1); // 数据结构现在包含 [1]
frequencyTracker.deleteOne(1); // 数据结构现在为空 []
frequencyTracker.hasFrequency(1); // 返回 false ,因为数据结构为空
示例 3:
输入 [“FrequencyTracker”, “hasFrequency”, “add”, “hasFrequency”]
[[], [2], [3], [1]]
输出
[null, false, null, true]
解释
FrequencyTracker frequencyTracker = new FrequencyTracker();
frequencyTracker.hasFrequency(2); // 返回 false ,因为数据结构为空
frequencyTracker.add(3); // 数据结构现在包含 [3]
frequencyTracker.hasFrequency(1); // 返回 true ,因为 3 出现 1 次
提示:
1 <= number <= 105
1 <= frequency <= 105
最多调用 add、deleteOne 和 hasFrequency 共计 2 * 105 次
题解:
方法:双哈希表
用哈希表 cnt 统计每个数的出现次数。
class FrequencyTracker {
private final Map<Integer, Integer> cnt = new HashMap<>(); // number 的出现次数
private final Map<Integer, Integer> freq = new HashMap<>(); // number 的出现次数的出现次数
public FrequencyTracker() {}
public void update(int number, int delta) {
int c = cnt.merge(number, delta, Integer::sum);
freq.merge(c - delta, -1, Integer::sum); // 去掉一个旧的 cnt[number]
freq.merge(c, 1, Integer::sum); // 添加一个新的 cnt[number]
}
public void add(int number) {
update(number, 1);
}
public void deleteOne(int number) {
if (cnt.getOrDefault(number, 0) > 0) {
update(number, -1);
}
}
public boolean hasFrequency(int frequency) {
return freq.getOrDefault(frequency, 0) > 0; // 至少有一个 number 的出现次数恰好为 frequency
}
}
分类题单
滑动窗口(定长/不定长/多指针)
二分算法(二分答案/最小化最大值/最大化最小值/第K小)
单调栈(矩形系列/字典序最小/贡献法)
网格图(DFS/BFS/综合应用)
位运算(基础/性质/拆位/试填/恒等式/贪心/脑筋急转弯)
图论算法(DFS/BFS/拓扑排序/最短路/最小生成树/二分图/基环树/欧拉路径)





灵神往期的高质量题解(精选)
22.网格图中最少访问的格子数
题目链接:2617. 网格图中最少访问的格子数
给你一个下标从 0 开始的 m x n 整数矩阵 grid 。你一开始的位置在 左上角 格子 (0, 0) 。
当你在格子 (i, j) 的时候,你可以移动到以下格子之一:
-
满足 j < k <= grid[i][j] + j 的格子 (i, k) (向右移动),或者
-
满足 i < k <= grid[i][j] + i 的格子 (k, j) (向下移动)。
请你返回到达 右下角 格子 (m - 1, n - 1) 需要经过的最少移动格子数,如果无法到达右下角格子,请你返回 -1 。
示例 1:
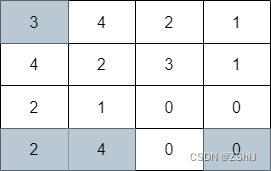
输入:grid = [[3,4,2,1],[4,2,3,1],[2,1,0,0],[2,4,0,0]]
输出:4
解释:上图展示了到达右下角格子经过的 4 个格子。
示例 2:
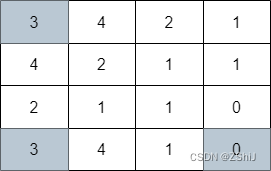
输入:grid = [[3,4,2,1],[4,2,1,1],[2,1,1,0],[3,4,1,0]]
输出:3
解释:上图展示了到达右下角格子经过的 3 个格子。
示例 3:

输入:grid = [[2,1,0],[1,0,0]]
输出:-1
解释:无法到达右下角格子。
提示:
m == grid.length
n == grid[i].length
1 <= m, n <= 105
1 <= m * n <= 105
0 <= grid[i][j] < m * n
grid[m - 1][n - 1] == 0
题解:
方法:单调栈优化 DP
class Solution {
public int minimumVisitedCells(int[][] grid) {
int m = grid.length;
int n = grid[0].length;
int mn = 0;
List<int[]>[] colStacks = new ArrayList[n]; // 每列的单调栈,为了能二分用 ArrayList
Arrays.setAll(colStacks, i -> new ArrayList<int[]>());
List<int[]> rowSt = new ArrayList<>(); // 行单调栈
for (int i = m - 1; i >= 0; i--) {
rowSt.clear();
for (int j = n - 1; j >= 0; j--) {
int g = grid[i][j];
List<int[]> colSt = colStacks[j];
mn = i < m - 1 || j < n - 1 ? Integer.MAX_VALUE : 1;
if (g > 0) {
// 在单调栈上二分
int k = search(rowSt, j + g);
if (k < rowSt.size()) {
mn = rowSt.get(k)[0] + 1;
}
k = search(colSt, i + g);
if (k < colSt.size()) {
mn = Math.min(mn, colSt.get(k)[0] + 1);
}
}
if (mn < Integer.MAX_VALUE) {
// 插入单调栈
while (!rowSt.isEmpty() && mn <= rowSt.get(rowSt.size() - 1)[0]) {
rowSt.remove(rowSt.size() - 1);
}
rowSt.add(new int[]{mn, j});
while (!colSt.isEmpty() && mn <= colSt.get(colSt.size() - 1)[0]) {
colSt.remove(colSt.size() - 1);
}
colSt.add(new int[]{mn, i});
}
}
}
return mn < Integer.MAX_VALUE ? mn : -1; // 最后一个算出的 mn 就是 f[0][0]
}
// 开区间二分,见 https://www.bilibili.com/video/BV1AP41137w7/
private int search(List<int[]> st, int target) {
int left = -1, right = st.size(); // 开区间 (left, right)
while (left + 1 < right) { // 区间不为空
int mid = left + (right - left) / 2;
if (st.get(mid)[1] <= target) {
right = mid; // 范围缩小到 (left, mid)
} else {
left = mid; // 范围缩小到 (mid, right)
}
}
return right;
}
}
方法:贪心+最小堆
类似 Dijkstra 算法
class Solution {
public int minimumVisitedCells(int[][] grid) {
int m = grid.length;
int n = grid[0].length;
int f = 0;
PriorityQueue<int[]>[] colHeaps = new PriorityQueue[n]; // 每一列的最小堆
Arrays.setAll(colHeaps, i -> new PriorityQueue<int[]>((a, b) -> a[0] - b[0]));
PriorityQueue<int[]> rowH = new PriorityQueue<>((a, b) -> a[0] - b[0]); // 行最小堆
for (int i = 0; i < m; i++) {
rowH.clear();
for (int j = 0; j < n; j++) {
while (!rowH.isEmpty() && rowH.peek()[1] < j) { // 无法到达第 j 列
rowH.poll(); // 弹出无用数据
}
PriorityQueue<int[]> colH = colHeaps[j];
while (!colH.isEmpty() && colH.peek()[1] < i) { // 无法到达第 i 行
colH.poll(); // 弹出无用数据
}
f = i > 0 || j > 0 ? Integer.MAX_VALUE : 1; // 起点算 1 个格子
if (!rowH.isEmpty()) {
f = rowH.peek()[0] + 1; // 从左边跳过来
}
if (!colH.isEmpty()) {
f = Math.min(f, colH.peek()[0] + 1); // 从上边跳过来
}
int g = grid[i][j];
if (g > 0 && f < Integer.MAX_VALUE) {
rowH.offer(new int[]{f, g + j}); // 经过的格子数,向右最远能到达的列号
colH.offer(new int[]{f, g + i}); // 经过的格子数,向下最远能到达的行号
}
}
}
return f < Integer.MAX_VALUE ? f : -1; // 此时的 f 是在 (m-1, n-1) 处算出来的
}
}
23.统计桌面上的不同数字
题目链接:2549. 统计桌面上的不同数字
给你一个正整数 n ,开始时,它放在桌面上。在 109 天内,每天都要执行下述步骤:
- 对于出现在桌面上的每个数字 x ,找出符合 1 <= i <= n 且满足 x % i == 1 的所有数字 i 。
- 然后,将这些数字放在桌面上。
返回在 109天之后,出现在桌面上的 不同 整数的数目。
注意:
- 一旦数字放在桌面上,则会一直保留直到结束。
- % 表示取余运算。例如,14 % 3 等于 2 。
示例 1:
输入:n = 5
输出:4
解释:最开始,5 在桌面上。
第二天,2 和 4 也出现在桌面上,因为 5 % 2 == 1 且 5 % 4 == 1 。
再过一天 3 也出现在桌面上,因为 4 % 3 == 1 。
在十亿天结束时,桌面上的不同数字有 2 、3 、4 、5 。
示例 2:
输入:n = 3
输出:2
解释:
因为 3 % 2 == 1 ,2 也出现在桌面上。
在十亿天结束时,桌面上的不同数字只有两个:2 和 3 。
提示:
1 <= n <= 100
题解:
方法:数学 O(1)
因为 n mod (n−1)=1 一定满足要求,所以我们可以从 n 开始,生成 n−1,n−2,⋯,最后 [2,n] 中的数字都会在桌面上,这有一共有 n−1 个。
注意特判 n=1 的情况,此时答案为 1。
class Solution {
public int distinctIntegers(int n) {
return Math.max(n - 1, 1);
}
}
24.零钱兑换
题目链接:322. 零钱兑换
给你一个整数数组 coins ,表示不同面额的硬币;以及一个整数 amount ,表示总金额。
计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额,返回 -1 。
你可以认为每种硬币的数量是无限的。
示例 1:
输入:coins = [1, 2, 5], amount = 11
输出:3
解释:11 = 5 + 5 + 1
示例 2:
输入:coins = [2], amount = 3
输出:-1
示例 3:
输入:coins = [1], amount = 0
输出:0
提示:
1 <= coins.length <= 12
1 <= coins[i] <= 231 - 1
0 <= amount <= 104
题解:
动态规划
方法:记忆化搜索(递归搜索 + 保存计算结果)
设计一个递归函数dfs用于计算凑齐金额c所需的最少硬币数量,其中i表示当前考虑的硬币种类。
在dfs函数中,若i小于0,说明没有硬币可用,若c等于0,表示已经凑齐了目标金额,返回0;否则返回一个较大的数(表示无解)。
若memo数组中已经保存了当前状态的结果,则直接返回memo[i][c]。
若c小于coins[i],说明当前硬币面额大于剩余金额,无法使用当前硬币,则返回dfs(i - 1, c)的结果。
否则,当前金额c可以使用当前硬币coins[i],比较不使用当前硬币和使用当前硬币的情况,取其中最小的结果。
class Solution {
private int[] coins; // 硬币面额数组
private int[][] memo; // 记忆化数组
// 构造函数,初始化coins数组和memo数组,并调用dfs函数求解最少硬币数量
public int coinChange(int[] coins, int amount) {
this.coins = coins;
int n = coins.length;
memo = new int[n][amount + 1];
for (int[] row : memo)
Arrays.fill(row, -1); // 初始化memo数组为-1
int ans = dfs(n - 1, amount); // 调用dfs函数求解最少硬币数量
return ans < Integer.MAX_VALUE / 2 ? ans : -1; // 返回结果,若无解则返回-1
}
// 递归函数,计算凑齐金额c所需的最少硬币数量
private int dfs(int i, int c) {
// 若i小于0,表示没有硬币可用;若c等于0,表示已凑齐目标金额,返回0;否则返回一个较大的数(表示无解)
if (i < 0) return c == 0 ? 0 : Integer.MAX_VALUE / 2;
// 若memo数组中已保存了当前状态的结果,则直接返回memo[i][c]
if (memo[i][c] != -1) return memo[i][c];
// 若c小于coins[i],当前硬币面额大于剩余金额,无法使用当前硬币,则返回dfs(i - 1, c)的结果
if (c < coins[i]) return memo[i][c] = dfs(i - 1, c);
// 否则,当前金额c可以使用当前硬币coins[i],比较不使用当前硬币和使用当前硬币的情况,取其中最小的结果
return memo[i][c] = Math.min(dfs(i - 1, c), dfs(i, c - coins[i]) + 1);
}
}
方法:递推
设计一个二维数组f,其中f[i][c]表示使用前i种硬币凑出金额c所需的最少硬币数量。
初始化f数组,将第一行的所有元素初始化为Integer.MAX_VALUE / 2,除了f[0][0]设为0,表示不需要硬币时的硬币数量为0。
通过状态转移方程更新f数组的值,即f[i][c] = min(f[i - 1][c], f[i][c - coins[i]] + 1)。
最终返回f[n][amount],即使用所有硬币凑出金额amount所需的最少硬币数量。
class Solution {
// 使用动态规划解决硬币找零问题
public int coinChange(int[] coins, int amount) {
int n = coins.length; // 获取硬币种类数量
int[][] f = new int[n + 1][amount + 1]; // 定义二维数组f,用于存储状态转移结果
Arrays.fill(f[0], Integer.MAX_VALUE / 2); // 初始化第一行的所有元素为Integer.MAX_VALUE / 2
f[0][0] = 0; // 设置f[0][0]为0,表示不需要硬币时的硬币数量为0
// 动态规划状态转移过程,更新f数组的值
for (int i = 0; i < n; ++i) {
for (int c = 0; c <= amount; ++c) {
if (c < coins[i]) { // 当前金额小于当前硬币面值时,不选当前硬币
f[i + 1][c] = f[i][c];
} else { // 否则,选取当前硬币或不选取当前硬币中的最小值
f[i + 1][c] = Math.min(f[i][c], f[i + 1][c - coins[i]] + 1);
}
}
}
int ans = f[n][amount]; // 获取使用所有硬币凑出金额amount所需的最少硬币数量
return ans < Integer.MAX_VALUE / 2 ? ans : -1; // 若最优解大于阈值,则返回-1
}
}
方法:空间优化:滚动数组
由于状态转移方程只涉及到上一行的值,因此可以使用滚动数组进行空间优化,只需两个一维数组。
设计两个一维数组f[2][amount + 1],用于存储状态转移结果。
初始化第一个一维数组f[0][],并且设置f[0][0]为0,表示不需要硬币时的硬币数量为0。
通过状态转移方程更新第二个一维数组f[(i + 1) % 2][]的值。
最终返回f[n % 2][amount],即使用所有硬币凑出金额amount所需的最少硬币数量。
class Solution {
// 使用动态规划解决硬币找零问题(空间优化:滚动数组)
public int coinChange(int[] coins, int amount) {
int n = coins.length; // 获取硬币种类数量
int[][] f = new int[2][amount + 1]; // 定义两个一维数组f,用于存储状态转移结果
Arrays.fill(f[0], Integer.MAX_VALUE / 2); // 初始化第一个一维数组的所有元素为Integer.MAX_VALUE / 2
f[0][0] = 0; // 设置f[0][0]为0,表示不需要硬币时的硬币数量为0
// 动态规划状态转移过程,通过滚动数组更新第二个一维数组的值
for (int i = 0; i < n; ++i) {
for (int c = 0; c <= amount; ++c) {
if (c < coins[i]) { // 当前金额小于当前硬币面值时,不选当前硬币
f[(i + 1) % 2][c] = f[i % 2][c];
} else { // 否则,选取当前硬币或不选取当前硬币中的最小值
f[(i + 1) % 2][c] = Math.min(f[i % 2][c], f[(i + 1) % 2][c - coins[i]] + 1);
}
}
}
int ans = f[n % 2][amount]; // 获取使用所有硬币凑出金额amount所需的最少硬币数量
return ans < Integer.MAX_VALUE / 2 ? ans : -1; // 若最优解大于阈值,则返回-1
}
}
方法:空间优化:一个数组
由于状态转移方程只涉及到前一个状态的值,因此可以只使用一个一维数组进行空间优化。
设计一个一维数组f,用于存储状态转移结果。
初始化数组f,将除0元外的所有金额的硬币数量初始化为无穷大(用Integer.MAX_VALUE / 2表示)。
将f[0]设置为0,表示不需要硬币时的硬币数量为0。
通过状态转移方程更新数组f的值,即f[c] = Math.min(f[c], f[c - x] + 1),其中x为当前硬币面值。
最终返回f[amount],即使用所有硬币凑出金额amount所需的最少硬币数量。
class Solution {
// 使用动态规划解决硬币找零问题(空间优化:一个数组)
public int coinChange(int[] coins, int amount) {
int[] f = new int[amount + 1]; // 定义一个一维数组f,用于存储状态转移结果
Arrays.fill(f, Integer.MAX_VALUE / 2); // 初始化除0元外的所有金额的硬币数量为无穷大(用Integer.MAX_VALUE / 2表示)
f[0] = 0; // 设置f[0]为0,表示不需要硬币时的硬币数量为0
// 动态规划状态转移过程,通过一维数组更新硬币数量的值
for (int x : coins) { // 遍历硬币面值数组
for (int c = x; c <= amount; ++c) { // 遍历金额范围
f[c] = Math.min(f[c], f[c - x] + 1); // 更新当前金额所需的最少硬币数量
}
}
int ans = f[amount]; // 获取使用所有硬币凑出金额amount所需的最少硬币数量
return ans < Integer.MAX_VALUE / 2 ? ans : -1; // 若最优解大于阈值,则返回-1
}
}
题单:动态规划(入门/背包/状态机/划分/区间/状压/数位/数据结构优化/树形/博弈/概率期望)
下接:【题解】—— LeetCode一周小结13





![[Java基础揉碎]final关键字](https://img-blog.csdnimg.cn/direct/8727d75b8df745cda248eef23ec0ae0a.png)
![[AIGC] SQL中的数据添加和操作:数据类型介绍](https://img-blog.csdnimg.cn/direct/e399561dbfb0408893f353f1a41d68a4.png)