513. 找树左下角的值

给定一个二叉树的 根节点 root，请找出该二叉树的 最底层 最左边 节点的值。

假设二叉树中至少有一个节点。

示例 1:

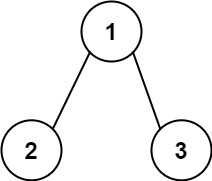
输入: root = [2,1,3]
输出: 1

示例 2:

输入: [1,2,3,4,null,5,6,null,null,7]
输出: 7

提示:

• 二叉树的节点个数的范围是 [1,104]
• -231 <= Node.val <= 231 - 1 

状态：完成，使用层序遍历

思路：层序遍历最后一层的第一个元素。

class Solution {
    public int findBottomLeftValue(TreeNode root) {
        Queue<TreeNode> queue =new LinkedList<>();
        ArrayList<List<Integer>> list =new ArrayList<>();
        queue.add(root);
        while(queue.size()>0){
            int size=queue.size();
            ArrayList<Integer> list2 =new ArrayList<>();
            for(int i=0;i<size;i++){
                TreeNode node =queue.poll();
                list2.add(node.val);
                if(node.left!=null) queue.add(node.left);
                if(node.right!=null) queue.add(node.right);
            }
            list.add(list2);
        }
        return list.get(list.size()-1).get(0);
    }
}

 112. 路径总和

给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在 根节点到叶子节点 的路径，这条路径上所有节点值相加等于目标和 targetSum 。如果存在，返回 true ；否则，返回 false 。

叶子节点 是指没有子节点的节点。

示例 1：

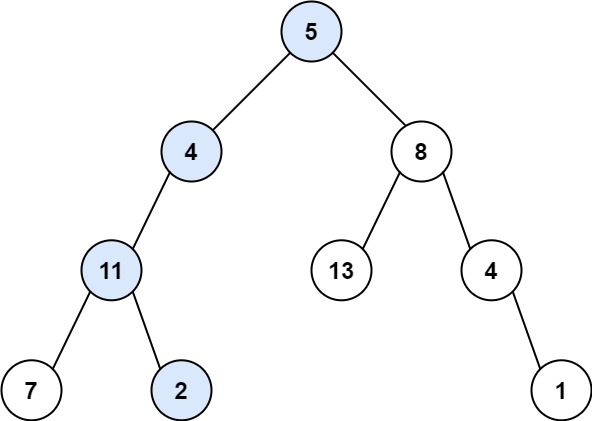
输入：root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22
输出：true
解释：等于目标和的根节点到叶节点路径如上图所示。

示例 2：

输入：root = [1,2,3], targetSum = 5
输出：false
解释：树中存在两条根节点到叶子节点的路径：
(1 --> 2): 和为 3
(1 --> 3): 和为 4
不存在 sum = 5 的根节点到叶子节点的路径。

示例 3：

输入：root = [], targetSum = 0
输出：false
解释：由于树是空的，所以不存在根节点到叶子节点的路径。

提示：

• 树中节点的数目在范围 [0, 5000] 内
• -1000 <= Node.val <= 1000
• -1000 <= targetSum <= 1000

 状态：完成

思路：遍历到叶子节点对比叶子节点跟目标值是否一直，如果一直说明该路径的总和跟目标值一直。该题使用前序遍历。

class Solution {
    public boolean hasPathSum(TreeNode root, int targetSum) {
        if(root==null&&targetSum==0) return false;
        if(root==null) return false;
        boolean flag =hasPathSum2(root,targetSum);
        return flag;
    }
    public boolean hasPathSum2(TreeNode root,int targetSum){
        if(root.left==null&&root.right==null&&root.val==targetSum) return true;
        boolean flag=false;
        if(root.left!=null){
            flag=hasPathSum2(root.left,targetSum-root.val);
        }
        if(flag) return flag;
        boolean flag2=false;
        if(root.right!=null){
            flag2=hasPathSum2(root.right,targetSum-root.val);
        }    
        if(flag2) return flag2;
        return false;
    }
}

106. 从中序与后序遍历序列构造二叉树

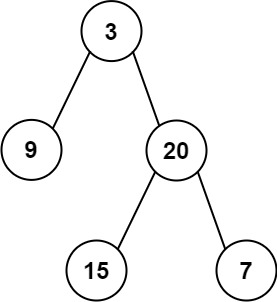
给定两个整数数组 inorder 和 postorder ，其中 inorder 是二叉树的中序遍历， postorder 是同一棵树的后序遍历，请你构造并返回这颗 二叉树 。

示例 1:

输入：inorder = [9,3,15,20,7], postorder = [9,15,7,20,3]
输出：[3,9,20,null,null,15,7]

示例 2:

输入：inorder = [-1], postorder = [-1]
输出：[-1]

提示:

• 1 <= inorder.length <= 3000
• postorder.length == inorder.length
• -3000 <= inorder[i], postorder[i] <= 3000
• inorder 和 postorder 都由 不同 的值组成
• postorder 中每一个值都在 inorder 中
• inorder 保证是树的中序遍历
• postorder 保证是树的后序遍历

 状态：完成

思路：后序遍历的最后一个字符就是该树的根节点，然后在中序遍历中根据这一特性划分左右子树完成题目。前序遍历就是第一个字符就是该树的根节点，同上完成。

class Solution {
    public TreeNode buildTree(int[] inorder, int[] postorder) {
        if(inorder.length==0) return null;
        int gen=postorder[inorder.length-1];
        TreeNode root=new TreeNode(gen);
        int index=0;
        for(int i=0;i<inorder.length;i++){
            if(inorder[i]==gen){
                index=i; 
                break;
            }
        }
        TreeNode left=buildTree(Arrays.copyOfRange(inorder,0,index),Arrays.copyOfRange(postorder,0,index));
        TreeNode right=buildTree(Arrays.copyOfRange(inorder,index+1,inorder.length),Arrays.copyOfRange(postorder,index,postorder.length-1));
        root.right=right;
        root.left=left;
        return root;
    }
}

根据前序跟中序：

class Solution {
    public TreeNode buildTree(int[] preorder, int[] inorder) {
        if(inorder.length==0) return null;
        int gen=preorder[0];
        TreeNode root=new TreeNode(gen);
        int index=0;
        for(int i=0;i<inorder.length;i++){
            if(inorder[i]==gen){
                index=i; 
                break;
            }
        }
        TreeNode left=null;
        TreeNode right=null;
        if(index>0)
        left=buildTree(Arrays.copyOfRange(preorder,1,index+1),Arrays.copyOfRange(inorder,0,index));
        if(index<inorder.length-1)
        right=buildTree(Arrays.copyOfRange(preorder,index+1,preorder.length),Arrays.copyOfRange(inorder,index+1,inorder.length));
        root.right=right;
        root.left=left;
        
        return root;
    }
}

感想：今天的题目比较靠基础和二叉树的特性，不会就比较难做了。周赛有个新的数据结构红黑树，这是个非严格的二叉搜索树可以进行排序，这个我还没搞明白。