强化学习笔记
主要基于b站西湖大学赵世钰老师的【强化学习的数学原理】课程,个人觉得赵老师的课件深入浅出,很适合入门.
第一章 强化学习基本概念
第二章 贝尔曼方程
第三章 贝尔曼最优方程
文章目录
- 强化学习笔记
- 一、最优策略
- 二、贝尔曼最优方程(BOE)
- 三、BOE的求解
- 1 求解方法
- 2 实例
- 四、BOE的最优性
- 参考资料
上一节讲了贝尔曼方程,这一节继续在贝尔曼方程的基础上讲贝尔曼最优方程,后面的策略迭代和值迭代算法都是根据贝尔曼最优方程来的.
一、最优策略
强化学习的最终目标是获得最优策略,所以有必要首先定义什么是最优策略。该定义基于状态值,比如,我们考虑两个给定策略
π
1
\pi_1
π1和
π
2
\pi_2
π2。若任一状态下
π
1
\pi_1
π1的状态值大于等于
π
2
\pi_2
π2的状态值,即:
v
π
1
(
s
)
≥
v
π
2
(
s
)
,
∀
s
∈
S
,
v_{\pi_1}(s)\geq v_{\pi_2}(s),\quad\forall s\in\mathcal{S},
vπ1(s)≥vπ2(s),∀s∈S,
那么我们称
π
1
\pi_1
π1是比
π
2
\pi_2
π2更好的策略.最优策略就是所有可能的策略中最好的,定义如下:
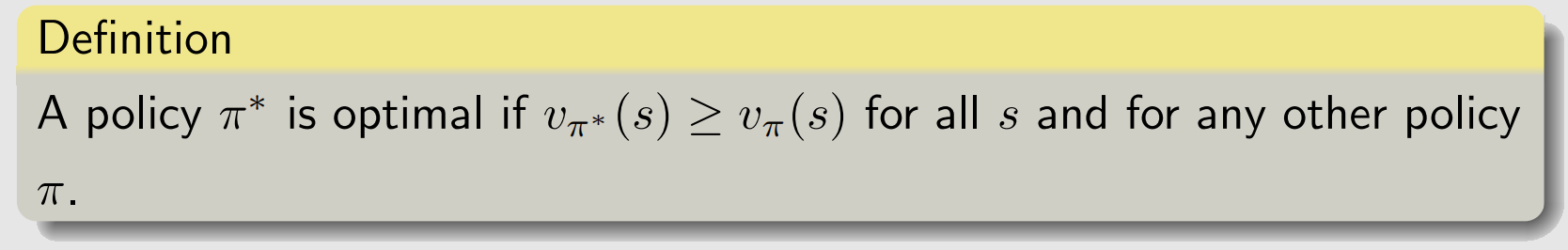
如何得到这个策略呢?需要求解贝尔曼最优方程.
二、贝尔曼最优方程(BOE)
贝尔曼最优方程(Bellman Optimal Equation,BOE),就是最优策略条件下的贝尔曼方程:
v
(
s
)
=
max
π
∑
a
π
(
a
∣
s
)
(
∑
r
p
(
r
∣
s
,
a
)
r
+
γ
∑
s
′
p
(
s
′
∣
s
,
a
)
v
(
s
′
)
)
,
∀
s
∈
S
=
max
π
∑
a
π
(
a
∣
s
)
q
(
s
,
a
)
s
∈
S
\begin{aligned} v\left(s\right)& =\max_{\pi}\sum_{a}\pi(a|s)\left(\sum_{r}p(r|s,a)r+\gamma\sum_{s'}p(s'|s,a)v(s')\right),\quad\forall s\in\mathcal{S} \\ &=\max_{\pi}\sum_{a}\pi\left(a|s\right)q\left(s,a\right)\quad s\in{\mathcal S} \end{aligned}
v(s)=πmaxa∑π(a∣s)(r∑p(r∣s,a)r+γs′∑p(s′∣s,a)v(s′)),∀s∈S=πmaxa∑π(a∣s)q(s,a)s∈S
注意:
- p ( r ∣ s , a ) , p ( s ′ ∣ s , a ) p(r|s,a),p(s^{\prime}|s,a) p(r∣s,a),p(s′∣s,a) 给定
- v ( s ) , v ( s ′ ) v(s),v(s^{\prime}) v(s),v(s′) 是需要计算的变量
- π \pi π为优化变量
我们可以发现贝尔曼最优方程存在两个未知数
v
v
v和
π
\pi
π,一个方程怎么求解两个未知数呢?我们以下列式子说明,是可以求解的。

也就是说在求解时,可以固定一个变量,先求max的变量.

受上面例子的启发,考虑到 ∑ a π ( a ∣ s ) = 1 \sum_a\pi(a|s)=1 ∑aπ(a∣s)=1,我们有:
υ
(
s
)
=
max
π
∑
a
π
(
a
∣
s
)
(
∑
r
p
(
r
∣
s
,
a
)
r
+
γ
∑
s
′
p
(
s
′
∣
s
,
a
)
v
(
s
′
)
)
,
=
max
π
∑
a
π
(
a
∣
s
)
q
(
s
,
a
)
=
max
a
∈
A
(
s
)
q
(
s
,
a
)
\begin{aligned} \upsilon(s)& \begin{aligned}=\max_{\color{red}{\pi}}\sum_{a}\pi(a|s)\left(\sum_{r}p(r|s,a)r+\gamma\sum_{s'}p(s'|s,a)v(s')\right),\end{aligned} \\ &=\max_{\color{red}{\pi}}\sum_{a}\color{red}{\pi(a|s)}q(s,a) \\ &=\max_{\color{red}{a\in\mathcal{A}(s)}}q(s,a) \end{aligned}
υ(s)=πmaxa∑π(a∣s)(r∑p(r∣s,a)r+γs′∑p(s′∣s,a)v(s′)),=πmaxa∑π(a∣s)q(s,a)=a∈A(s)maxq(s,a)
我们通过先对
π
\pi
π变量求max,最后将问题转换为:
v
(
s
)
=
max
a
∈
A
(
s
)
q
(
s
,
a
)
v(s)=\max_{\color{red}{a\in\mathcal{A}(s)}}q(s,a)
v(s)=a∈A(s)maxq(s,a)而这个方程与
π
\pi
π无关了,只有一个变量,那就是
v
(
s
)
v(s)
v(s)(向量形式),如何求解这个方程呢?下面介绍如何用迭代法进行求解.
三、BOE的求解
1 求解方法
我们考虑BOE的向量形式:
v
=
f
(
v
)
=
max
π
(
r
π
+
γ
P
π
v
)
v=f(v)=\max_{\pi}(r_\pi+\gamma P_\pi v)
v=f(v)=πmax(rπ+γPπv)而这个函数
f
f
f是一个压缩映射,压缩常数为
γ
\gamma
γ,证明见参考资料1的对应章节。什么是压缩映射?
定义(压缩映射)
如果存在 α ∈ ( 0 , 1 ) \alpha\in(0,1) α∈(0,1),使得函数 g g g对 ∀ x 1 , x 2 ∈ dom g \forall x_1,x_2\in \operatorname{dom} g ∀x1,x2∈domg满足
∥ g ( x 1 ) − g ( x 2 ) ∥ ≤ α ∥ x 1 − x 2 ∥ \|g(x_1)-g(x_2)\|\leq\alpha\|x_1-x_2\| ∥g(x1)−g(x2)∥≤α∥x1−x2∥则我们称 g g g为一个压缩映射,称常数 α \alpha α为压缩常数.
f f f是压缩映射有什么用呢?这里需要先介绍一下压缩映射原理.
定理(压缩映射原理)
设 g g g是 [ a , b ] [a,b] [a,b] 上的一个压缩映射,则
- g g g在 [ a , b ] [ a, b] [a,b] 中存在唯一的不动点 ξ = g ( ξ ) \xi=g\left(\xi\right) ξ=g(ξ) ;
- 由任何初始值 x 0 ∈ [ a , b ] x_0\in[a,b] x0∈[a,b] 和递推公式
x n + 1 = g ( x n ) , n ∈ N ∗ x_{n+1}=g\left(x_n\right),n\in N^* xn+1=g(xn),n∈N∗ 生成的数列 { x n } \{x_n\} {xn} 一定收敛于 ξ \xi ξ.
这也就是说,压缩映像原理给出了一个求不动点的方法,而BOE的 f f f是压缩映射,因此我们有

具体来看每一次迭代怎么算:

当我们计算每个状态
s
s
s时,我们由
v
k
(
s
′
)
v_k(s')
vk(s′)可以计算得到
q
k
(
s
,
a
)
q_k(s,a)
qk(s,a),然后再求最大就得到
v
k
+
1
(
s
)
v_{k+1}(s)
vk+1(s)了。值得注意的是上述方程右端取得最优值时,我们有:
π
k
+
1
(
a
∣
s
)
=
{
1
a
=
a
∗
,
0
a
≠
a
∗
.
\pi_{k+1}(a|s)=\begin{cases} 1 & a=a^*,\\ 0 & a\neq a^*. \end{cases}
πk+1(a∣s)={10a=a∗,a=a∗.其中
a
∗
=
arg
max
a
q
k
(
s
,
a
)
a^*=\arg\max\limits_a q_k(s,a)
a∗=argamaxqk(s,a),这个策略被称为greedy policy,也就是每次都选择动作值(q值)最大的动作.
Note:
- 值得注意的是,任意给 v 0 ∈ dom f v_0\in\operatorname{dom} f v0∈domf,都能收敛到不动点.
2 实例
我们考虑如下这样一个问题,还是智能体走格子:
- 状态集: s 1 , s 2 , s 3 s_1,s_2,s_3 s1,s2,s3其中 s 2 s_2 s2是目标状态.
- 动作集: a l , a 0 , a r a_l,a_0,a_r al,a0,ar分别代表向左、原地不动、向右.
- 奖励:进入 s 2 s_2 s2+1,走出格子-1。
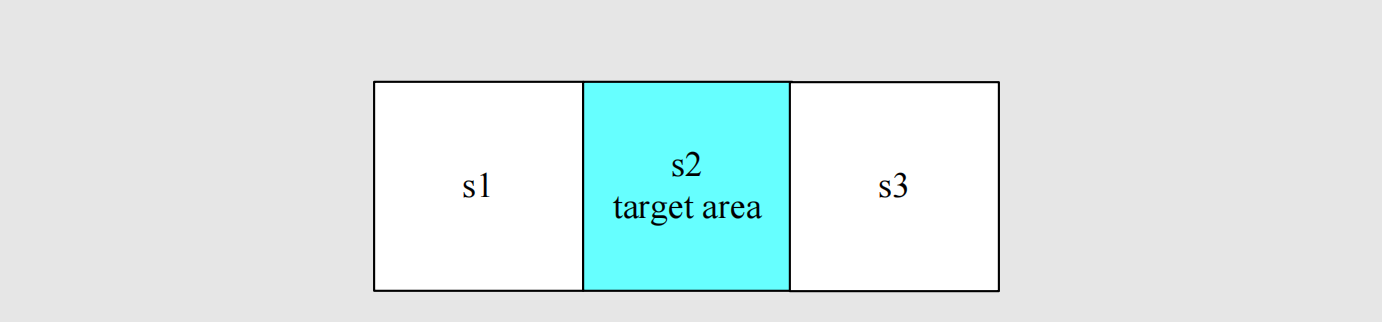
回顾上一章讲动作值函数和状态值函数的关系,我们可以写出
q
(
s
,
a
)
q(s,a)
q(s,a)与
v
(
s
)
v(s)
v(s)的关系:

下面给定一个
v
(
s
)
v(s)
v(s)的初始值,进行迭代:

显然,从直观上我们知道当前策略已经是最好的了。如果继续进行迭代,得到的策略不会再改变了,那么迭代算法怎么停止呢?停止准则可以通过如下公式进行判断:
∥
v
k
+
1
−
v
k
∥
≤
ϵ
\|v_{k+1}-v_k\|\leq\epsilon
∥vk+1−vk∥≤ϵ其中
ϵ
\epsilon
ϵ是一个给定的很小的值,也就是相邻两次
v
v
v相差很小时,我们认为
v
v
v已经逼近精确值了.
四、BOE的最优性
上面介绍怎么求解BOE的过程中,我们同时通过greedy policy的方法得到了最优策略:
π
∗
=
arg
max
π
(
r
π
+
γ
P
π
v
∗
)
\pi^*= \arg\max\limits_\pi (r_\pi+\gamma P_\pi v^*)
π∗=argπmax(rπ+γPπv∗)其中
v
∗
v^*
v∗是
π
∗
\pi^*
π∗对应的状态值,那么求解贝尔曼最优方程得到的这个
π
∗
\pi^*
π∗是不是最优策略呢?有如下定理进行保证.
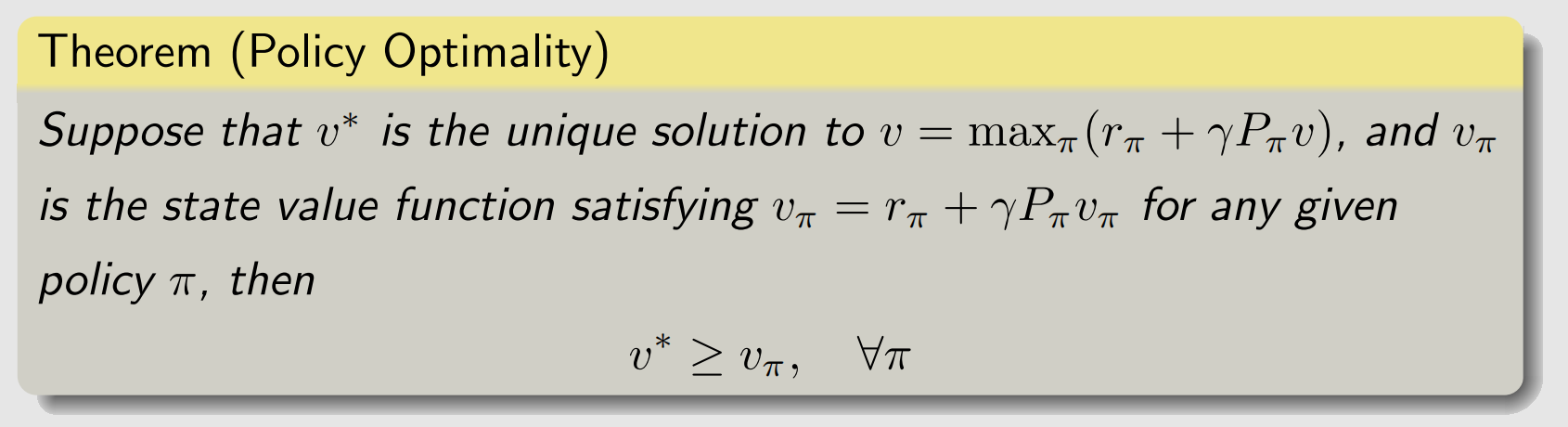
这个定理保证了,我们通过求解BOE得到的策略是最优策略,证明见参考资料1的对应章节.

参考资料
- Zhao, S. Mathematical Foundations of Reinforcement Learning. Springer Nature Press and Tsinghua University Press.
- Sutton, Richard S., and Andrew G. Barto. Reinforcement learning: An introduction. MIT press, 2018.
![每日一题 --- 两两交换链表中的节点[力扣][Go]](https://img-blog.csdnimg.cn/direct/2a9479e8da8145c2bebb3303d1e20290.png)



![[leetcode] 240. 搜索二维矩阵 II](https://img-blog.csdnimg.cn/direct/a5a6570d40564dc3b6873b84f3a7ab62.png)