1.什么是随机试验(random trial)?
如果一个试验满足试验可以在相同的条件下重复进行、试验所有可能结果明确可知(或者是可知这个范围)、每一次试验前会出现哪个结果事先并不确定,那么试验称为随机试验。
2.什么是随机事件?
在一次试验中可能出现,也可能不出现的结果称为随机事件,简称事件。随机事件本质是一个事件集合,总是由若干个基本事件构成。
3.什么是样本空间(sample space)?
一次试验的可能结果称为样本点,样本点组成的全体集合为样本空间。由一个样本点构成的事件称为基本事件。
4.什么是事件相容?
事件A与B相容就是说,事件A和事件B存在一些同时发生的事件。事件互斥是说事件A与B不存在同时发生的事件。事件对立是指事件A不发生的事件称为事件A的逆事件或者对立事件。对立事件一定是互斥事件,但是互斥事件不一定是对立事件。
5.什么是完备事件组?
如果 (样本空间)并且
,则称有限个事件
构成一个完备事件组。
6.什么是概率(probability)?
描述性定义:通常将事件A发生的可能性大小的度量称为事件A发生的概率,记为P(A)
统计性定义:统计性定义提供一种用频率估计概率的方法,在相同条件下做重复试验,事件A出现的次数k和总的试验次数n之比k/n称为事件A在这n次试验中出现的频率。当n充分大时,频率将趋近于某个常数p,这个常数p就称为这个事件A的概率。
公理化定义:设随机试验的样本空间为,如果对每一个事件A都有一个确定的实数P(A),且事件函数满足P(A)>=0,P(
)=1,可列可加性则称P(A)为A的概率。
7.什么是古典概型?
随机试验的样本空间满足(1)只有有限个样本点(基本事件)(2)每个样本点(基本事件)发生的可能性都一样。
8.什么是几何概型?
随机试验的样本空间满足(1)样本空间是一个可度量的有界区域(2)每个样本点发生的可能性都一样,即样本点落入
的某一可度量的子区域S的可能性大小与S的集合度量成正比,而与S的位置及形状无关。
9.概率有哪些性质?
(1)有界性:对于任一事件A,有0<=P(A)<=1,且P(空)=0,P(A)=1
(2)单调性:设A、B是两个事件 ,如果B包含A,则有P(B)>=P(A)
10.概率的一些公式?

![]()

全概率公式用于计算,某个结果B发生的可能性大小,这个结果的发生与多个“原因”Ai相联系。贝叶斯公式是在“结果”B发生的条件下,探求这一结果发生的原因,即Ai发生的可能性大小。
11.什么是事件的独立性?
设A,B为两个事件,如果P(AB)=P(A)*P(B),则称A与B相互独立
12.什么是n重伯努利概型?
在同样条件下独立重复地进行n次完全相同独立的试验,即每次试验的结果以及可能发生的概率不变,每次试验只有两个结果A和,则这种模型称为n重伯努利模型。X表示n重伯努利概型中事件A发生的次数,则X服从二项分布B(n,p)。
13.什么是随机变量(random variable)?
表示随机试验各种结果的实值单值函数,随机试验不论是否与数量相关都可以数量化,即都能用数量化的方式表达。
14.什么是分布函数?
x是一个实数,X是一个随机变量,则称F(x)=P{X<=x}为随机变量X的分布函数,则称X服从F(x)分布。主要性质有:F(x)是单调不减函数,是右连续函数,负无穷=0且正无穷=1
15.什么是离散型随机变量?
如果随机变量X只可能取有限个或可列无限个值x1,x2,x3...,则称x为离散型随机变量。
16.什么是连续型随机变量?
一个随机变量X的概率分布能被一个非负函数fX(称之为概率密度函数 probablility density function PDF)描述,满足

fX>=0,对fX在负无穷到正无穷上积分=1。对任意实数c有P{X=c}=0。
概率的几何意义:对于连续型随机变量落入某一区间的概率即{a<X<b}等于该区间上概率密度曲线下曲边梯形的面积。
17.有哪些离散型变量的分布?
- Bernoulli 0-1分布B(1,p):概率分布为P{X=1}=p,P{X=0}=1-p,则称X服从参数为p的0-1分布。
- BinomialDistribution 二项分布B(n,p):概率分布为
 ,则称X服从参数为(n,p)的二项分布。
,则称X服从参数为(n,p)的二项分布。 - Poissondistribution泊松分布P(λ):概率分布为

- 注意:当n>=20,p<=0.05时,可以用泊松近似公式λ=np逼近二项分布。
- Geometric distribution几何分布:概率分布为
,则称X服从参数为p的几何分布。
- HypergeometricDistribution超几何分布:概率分布为
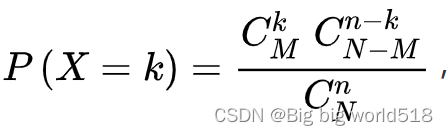 ,则称X服从参数为(n,N,M)的超几何分布。
,则称X服从参数为(n,N,M)的超几何分布。
18.有哪些连续型变量的分布?
- UniformDIstribution均匀分布U(a,b):如果随机变量X的概率密度函数,分布函数如下图所示。则称X在区间(a,b)上服从均匀分布。

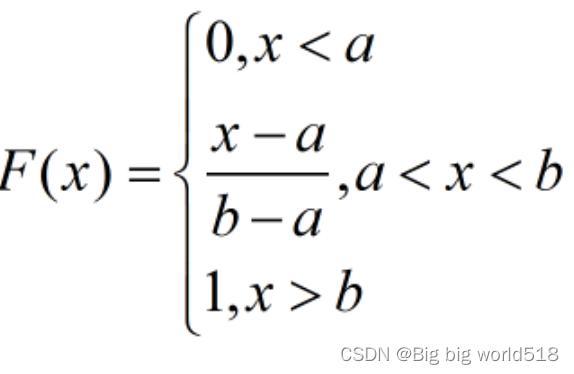
- ExponentialDistribution指数分布:如果X的概率密度和分布函数分别为如下函数,则称X服从参数为λ的指数分布。
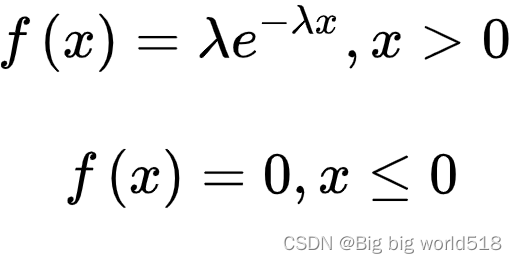

- Uniform Distribution正态分布:如果X的概率密度函数为下图,那么说X服从
的正态分布。
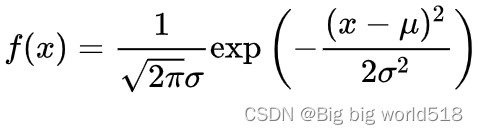
服从(0,1)的正态分布称为标准正态分布。