一、神经网络基本概念
神经网络可以分为生物神经网络和人工神经网络
(1)生物神经网络,指的是生物脑内的神经元、突触等构成的神经网络,可以使生物体产生意识,并协助生物体思考、行动和管理各机体活动。
(2)人工神经网络,是目前热门的深度学习的研究基础。目前对人工神经网络的定义多种多样,本书采用TKohonen1988年在NeuralNetworks 创刊号上给出的定义,即:“人工神经网络是由具有适应性的简单单元组成的广泛并行互连的网络,它能够模拟生物神经系统对真实世界物体所做出的交互反应”(Kohonen,1988)
二、最初的神经网络模型——M-P模型
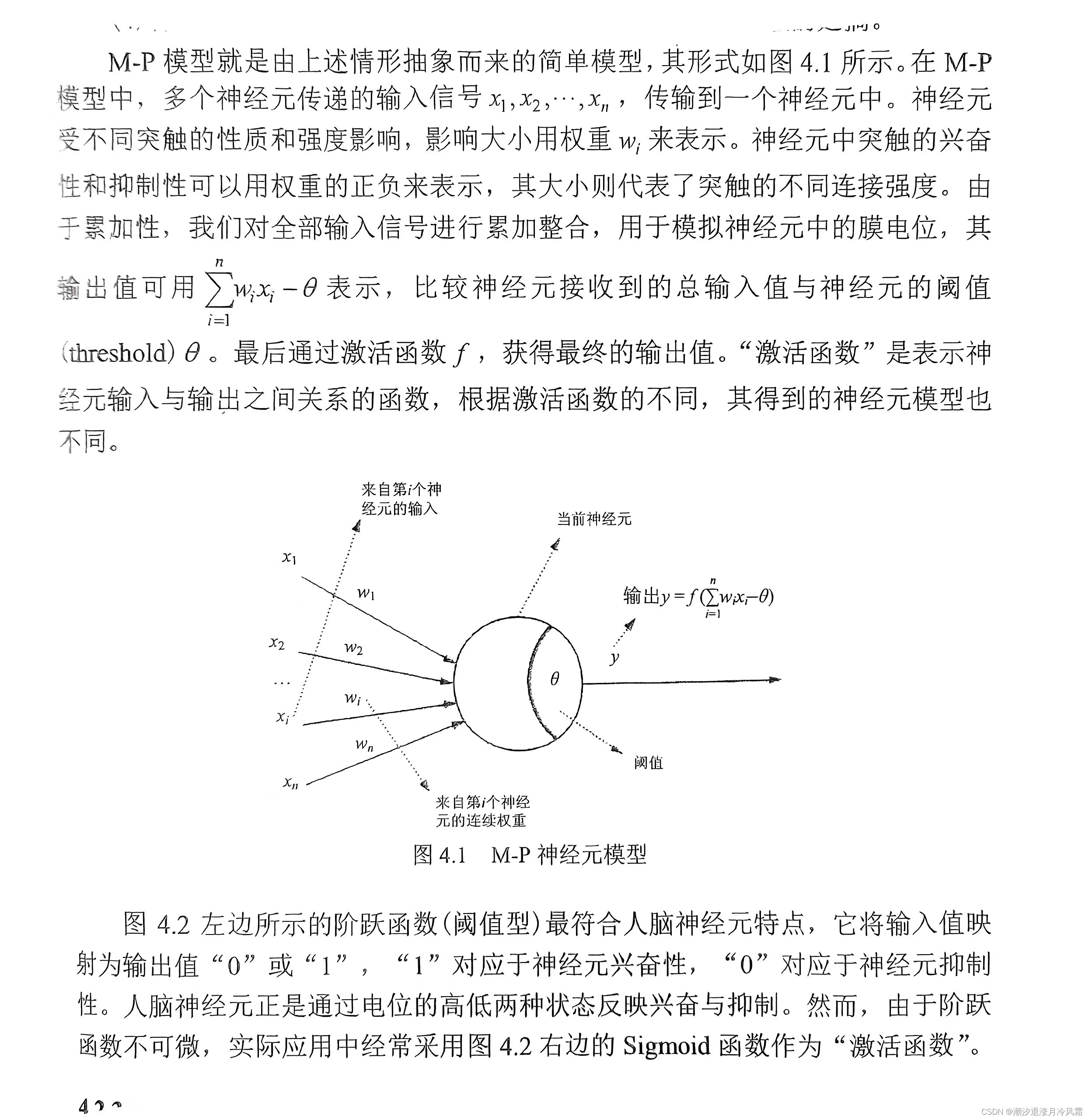
回忆生物神经元的结构,细胞体作为神经元的主体,由细胞体向外延伸的多个突起神经纤维称为树突,树突作为细胞体的输入端,轴突为细胞体向外延伸最长的突起,末端由很多细的分支被称为神经末梢,每一条神经末梢相当于细胞体的输出端。每个神经元通过轴突的神经末梢与其他神经元的细胞体或树突相连接,这种连接称为突触。
细胞体的细胞膜在正常状态下形成内负外正的膜电位,当神经元突触与上千个其他神经元连接时,接受不同输入对神经元点位的影响也不用(视为不同输入具有权重),当膜电位升高到一个阈值时,就会产生一个脉冲。突触也可以分为兴奋性和抑制性两种,兴奋性的突触可能引起下一个神经元兴奋,否则会抑制下一个神经元的兴奋。
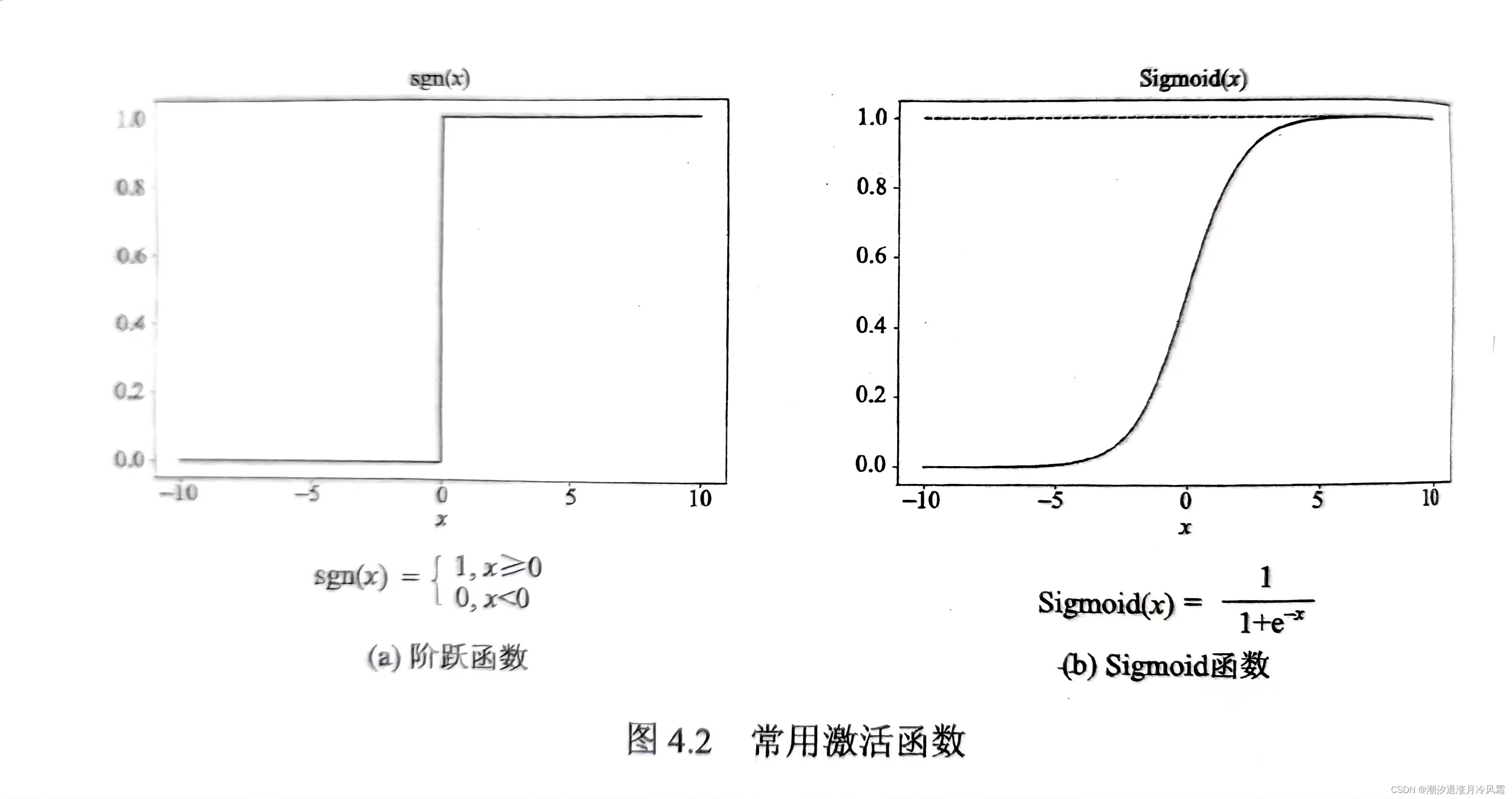
M-P模型就是模拟生物神经元模型建立的数学神经元模型,多个输入各自具有权重,神经元本身就有一个阈值,输出值由输入权和减去阈值通过激活函数f得到。激活函数通常是当输入权和大于阈值时输出响应。
三、感知机模型
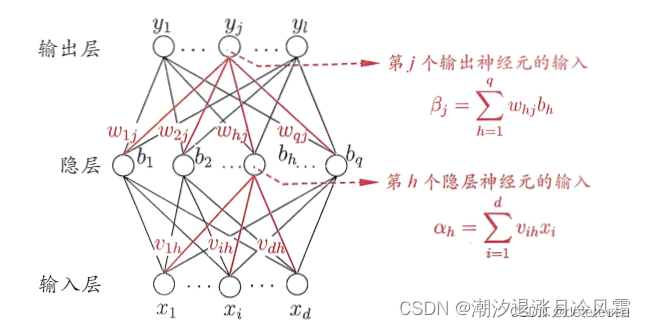
感知机模型以M-P模型为基础,但是能通过“学习“确定输入的权重和神经元的阈值。如果在输入层和输出层添加隐层,形成多层映射网络那就由单层感知机形成多层感知机。
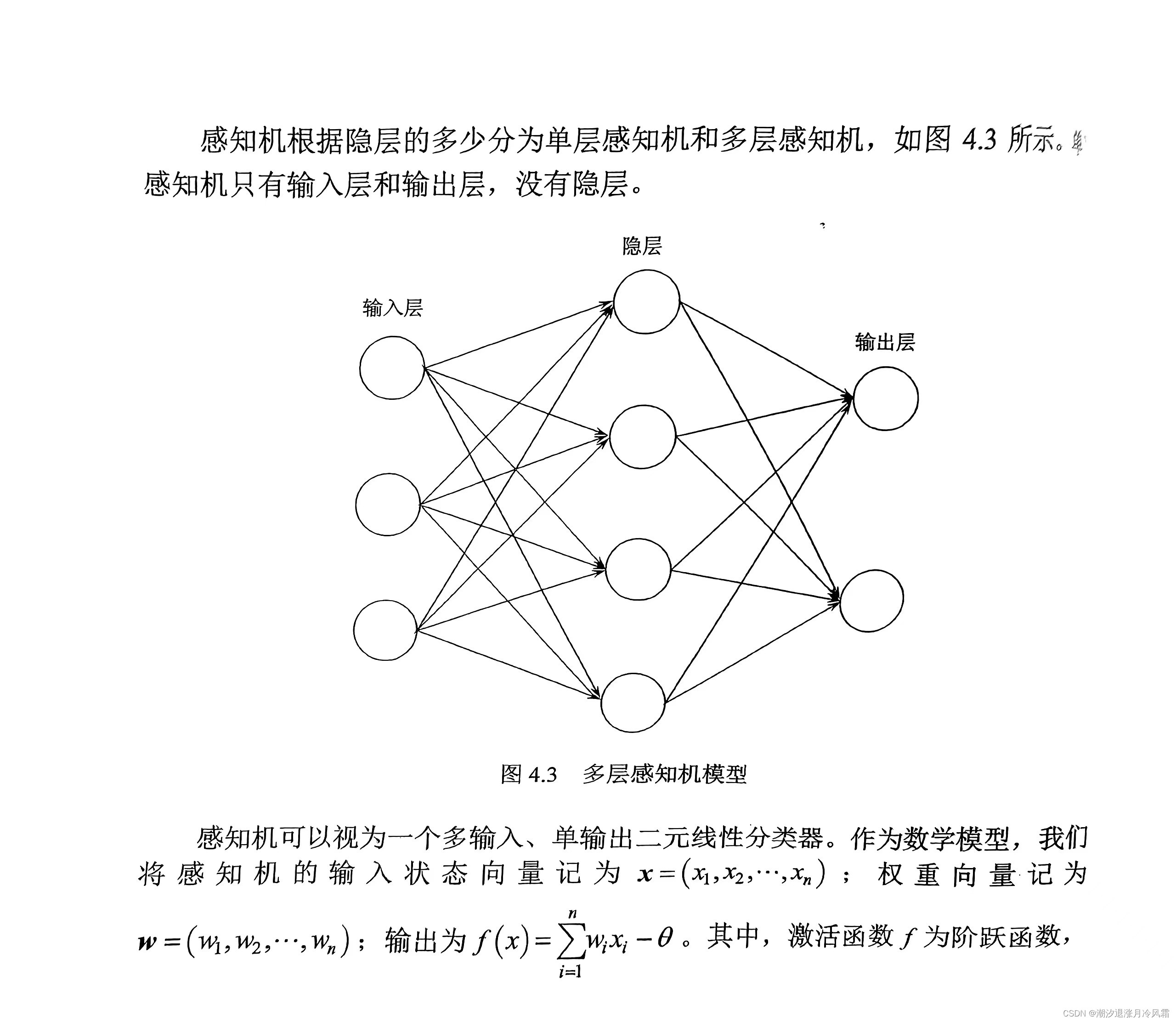
学习修正的过程并不复杂,对于真实值和预测值引入损失函数,通过最小化损失函数(类比最小二乘确定系数a、b),不断修正w、θ,得到最优的输出结果。

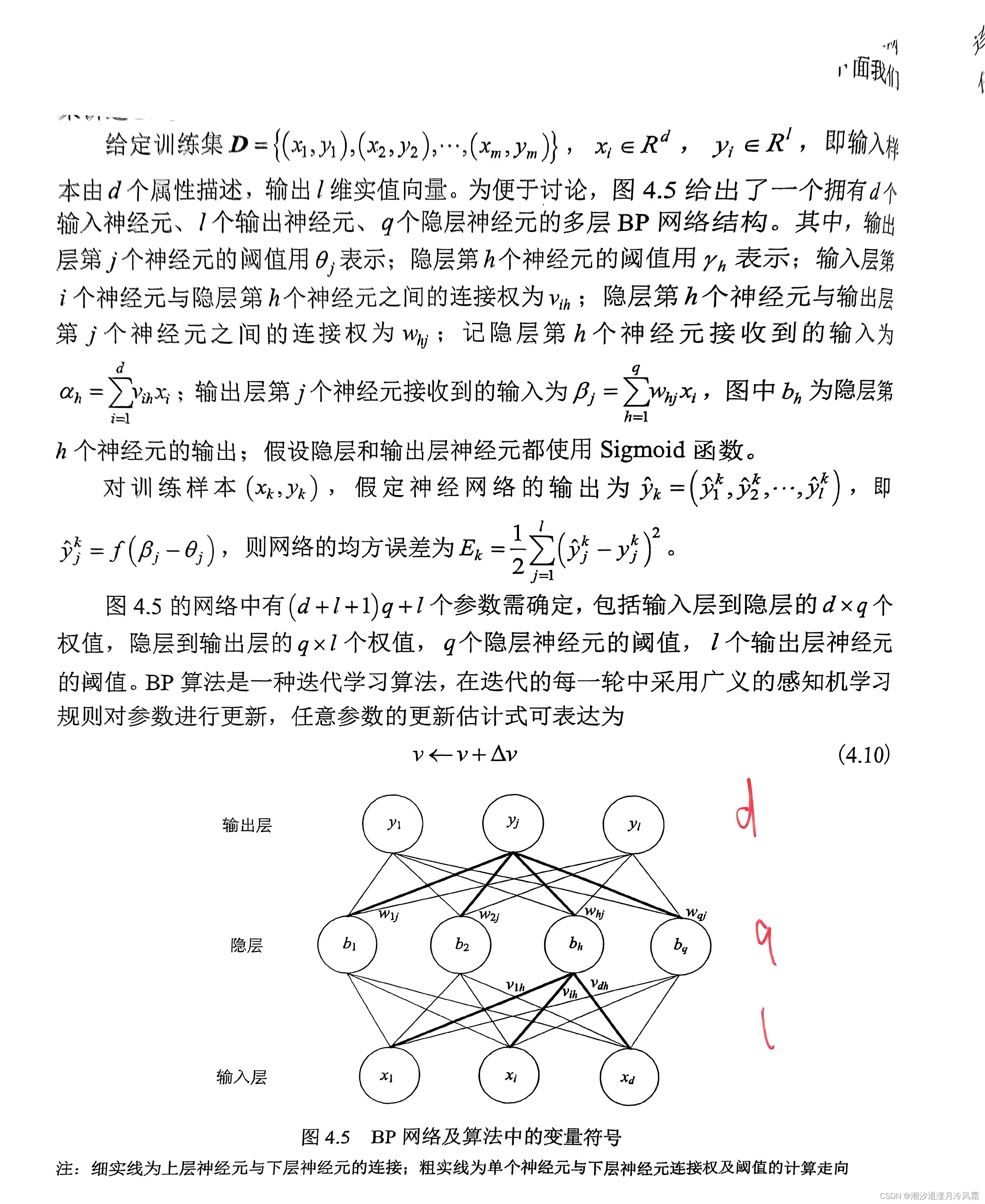
四、BP神经网络
下面介绍最成功的神经网络之一:BP神经网络,BP即back propagation(误差逆传递)
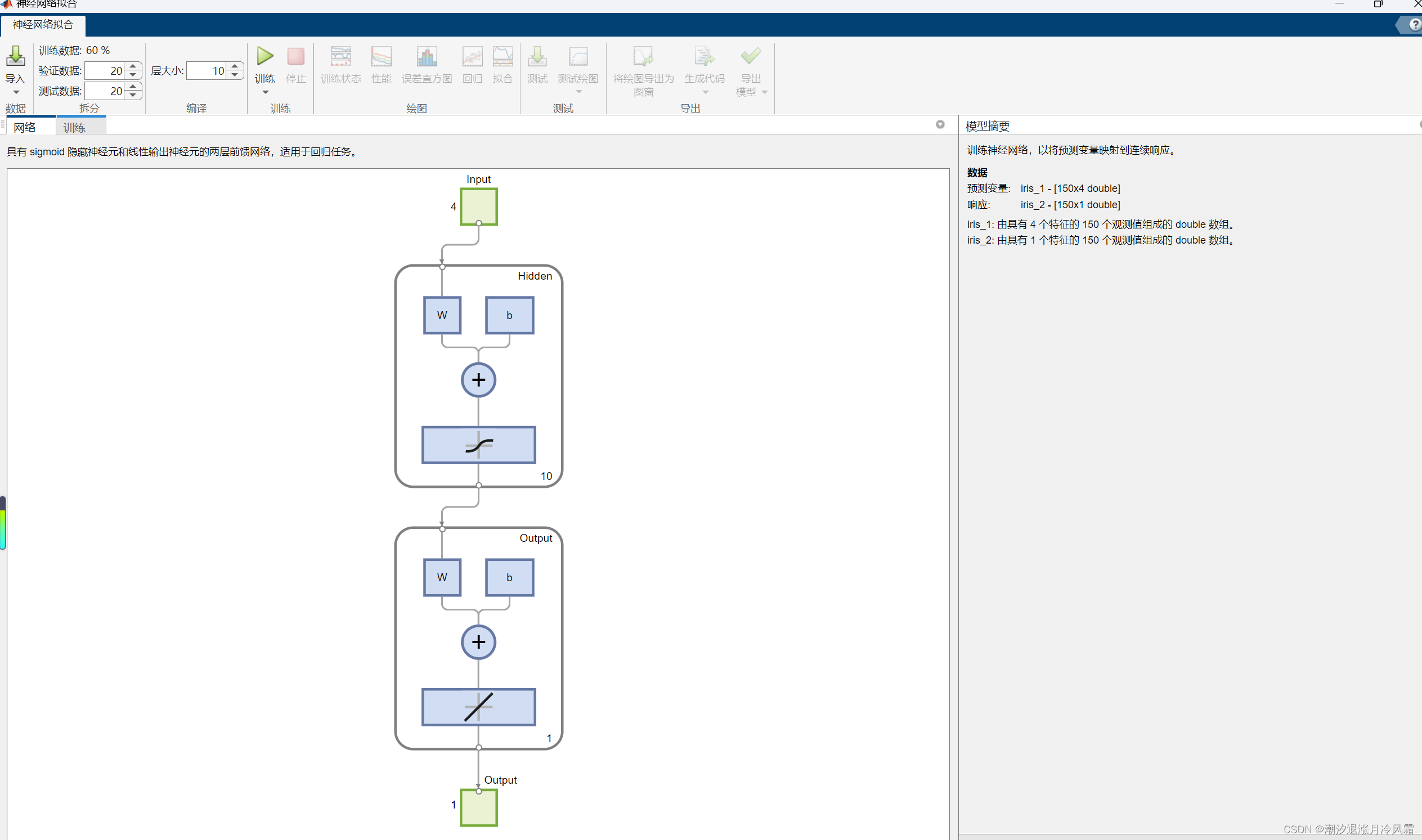


% Solve an Input-Output Fitting problem with a Neural Network
% Script generated by Neural Fitting app
% Created 23-Mar-2024 10:31:29
%
% This script assumes these variables are defined:
%
% iris_1 - input data.
% iris_2 - target data.
x = iris_1';
t = iris_2';
% Choose a Training Function
% For a list of all training functions type: help nntrain
% 'trainlm' is usually fastest.
% 'trainbr' takes longer but may be better for challenging problems.
% 'trainscg' uses less memory. Suitable in low memory situations.
trainFcn = 'trainlm'; % Levenberg-Marquardt backpropagation.
% Create a Fitting Network
hiddenLayerSize = 10;
net = fitnet(hiddenLayerSize,trainFcn);
% Setup Division of Data for Training, Validation, Testing
net.divideParam.trainRatio = 60/100;
net.divideParam.valRatio = 20/100;
net.divideParam.testRatio = 20/100;
% Train the Network
[net,tr] = train(net,x,t);
% Test the Network
y = net(x);
e = gsubtract(t,y);
performance = perform(net,t,y)
% View the Network
view(net)
% Plots
% Uncomment these lines to enable various plots.
%figure, plotperform(tr)
%figure, plottrainstate(tr)
%figure, ploterrhist(e)
%figure, plotregression(t,y)
%figure, plotfit(net,x,t)