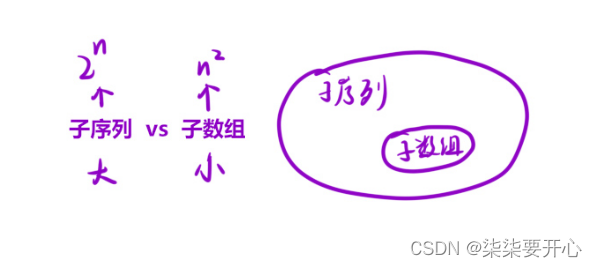
文章目录
- 1. 最长湍流子数组
- 题干:
- 算法原理:
- 1. 状态表示:
- 2. 状态转移方程
- 3. 初始化
- 4. 填表顺序
- 5. 返回值
- 代码:
- 2. 最长递增子序列
- 题干:
- 算法原理:
- 1. 状态表示:
- 2. 状态转移方程
- 3. 初始化
- 4. 填表顺序
- 5. 返回值
- 代码:
- 3. 摆动序列
- 题干:
- 算法原理:
- 1. 状态表示:
- 2. 状态转移方程
- 3. 初始化
- 4. 填表顺序
- 5. 返回值
- 代码:
- 4. 二叉树剪枝
- 题干:
- 算法原理:
- 代码:
- 5. 验证二叉搜索树
- 题干:
- 算法原理:
- 代码:
1. 最长湍流子数组

原题链接
题干:
返回 最大湍流子数组的长度
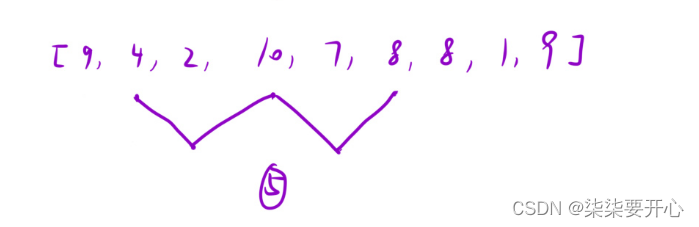
这里来解释一下什么是湍流数组
当数组呈现,前面大于中间,中间小于后面 的时候
算法原理:
1. 状态表示:
f[i] 表示:以 i 位置元素为结尾的所有子数组中,最后呈现「上升状态」下的最长湍流数组的长度
g[i] 表示:以 i 位置元素为结尾的所有子数组中,最后呈现「下降状态」下的最长湍流数组的长度
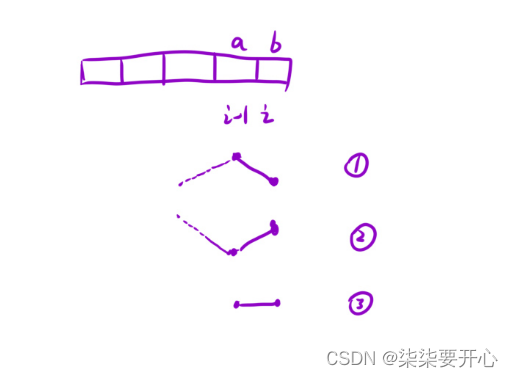
2. 状态转移方程

3. 初始化
所有的元素「单独」都能构成⼀个湍流数组,因此可以将 dp 表内所有元素初始化为 1
由于用到前面的状态,因此我们循环的时候从第⼆个位置开始即可
4. 填表顺序
从左往右,两个表⼀起填
5. 返回值
两个 dp 表里面的最大值
代码:
class Solution {
public int maxTurbulenceSize(int[] arr) {
int n = arr.length;
int[] f = new int[n];
int[] g = new int[n];
for(int i = 0; i < n; i++) {
f[i] = g[i] = 1;
}
int ret = 1;
for(int i = 1; i < n; i++) {
if(arr[i - 1] < arr[i]) {
f[i] = g[i - 1] + 1;
}else if(arr[i - 1] > arr[i]) {
g[i] = f[i - 1] + 1;
}
ret = Math.max(ret, Math.max(f[i], g[i]));
}
return ret;
}
}
2. 最长递增子序列

原题链接
题干:
给你一个整数数组 nums ,找到其中最长严格递增子序列的长度
算法原理:
1. 状态表示:
dp[i] 表示:以 i 元素为结尾的所有子序列中,最长递增子序列的长度
2. 状态转移方程
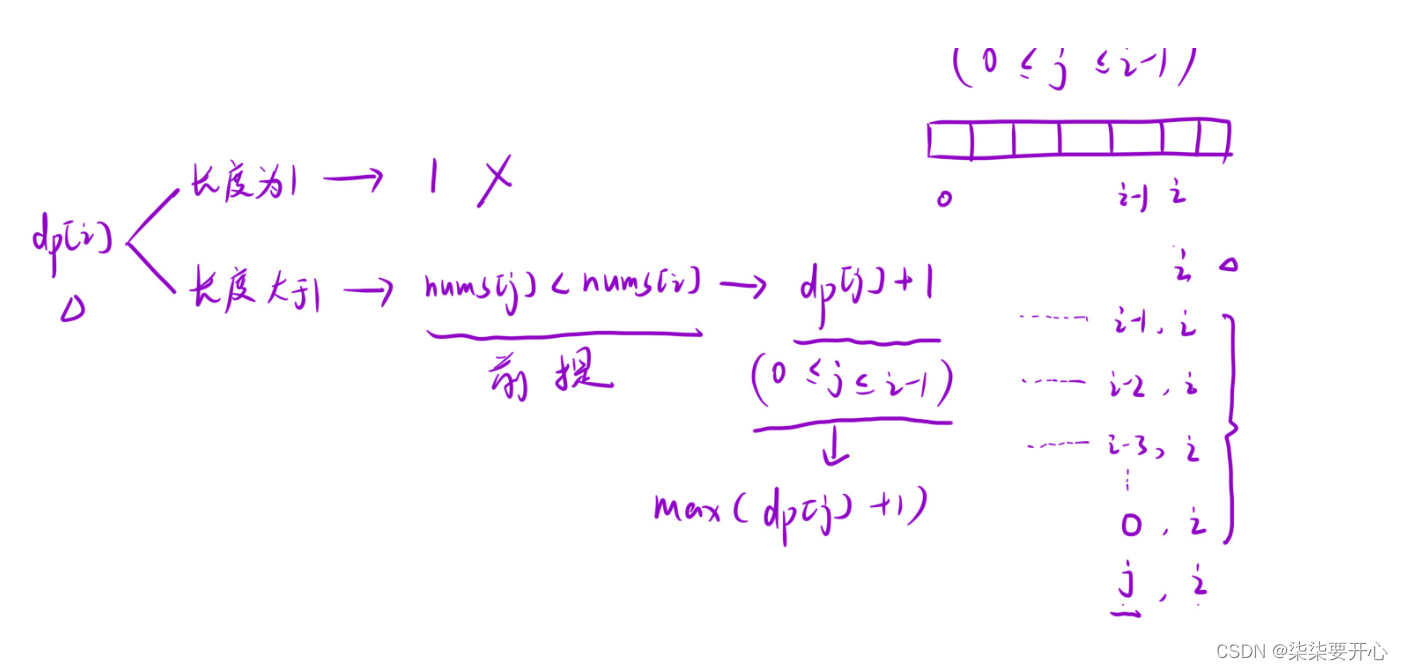
3. 初始化
dp 表里面所有值初始化为 1
4. 填表顺序
从左往右
5. 返回值
dp 表中的最大值
代码:
class Solution {
public int lengthOfLIS(int[] nums) {
int n = nums.length;
int[] dp = new int[n];
for(int i = 0; i < n; i++) {
dp[i] = 1;
}
int ret = 1;
for(int i = 0; i < n; i++) {
for(int j = 0; j < i; j++) {
if(nums[j] < nums[i]) {
dp[i] = Math.max(dp[j] + 1, dp[i]);
}
}
ret = Math.max(ret, dp[i]);
}
return ret;
}
}
3. 摆动序列

原题链接
题干:
如果连续数字之间的差严格地在正数和负数之间交替,则数字序列称为 摆动序列
第一个差(如果存在的话)可能是正数或负数。仅有一个元素或者含两个不等元素的序列也视作摆动序列。
算法原理:
1. 状态表示:
dp[i] 表示:「以 i 位置为结尾的最⻓摆动序列的⻓度」
如果状态表⽰这样定义的话,以 i 位置为结尾的最⻓摆动序列的⻓度我们没法从之前的状态推导出来
因此我们需要两个 dp 表:
f[i] 表⽰:以 i 位置元素为结尾的所有的⼦序列中,最后⼀个位置呈现「上升趋势」的最⻓摆动序列的⻓度
g[i] 表⽰:以 i 位置元素为结尾的所有的⼦序列中,最后⼀个位置呈现「下降趋势」的最⻓摆动序列的⻓度
2. 状态转移方程
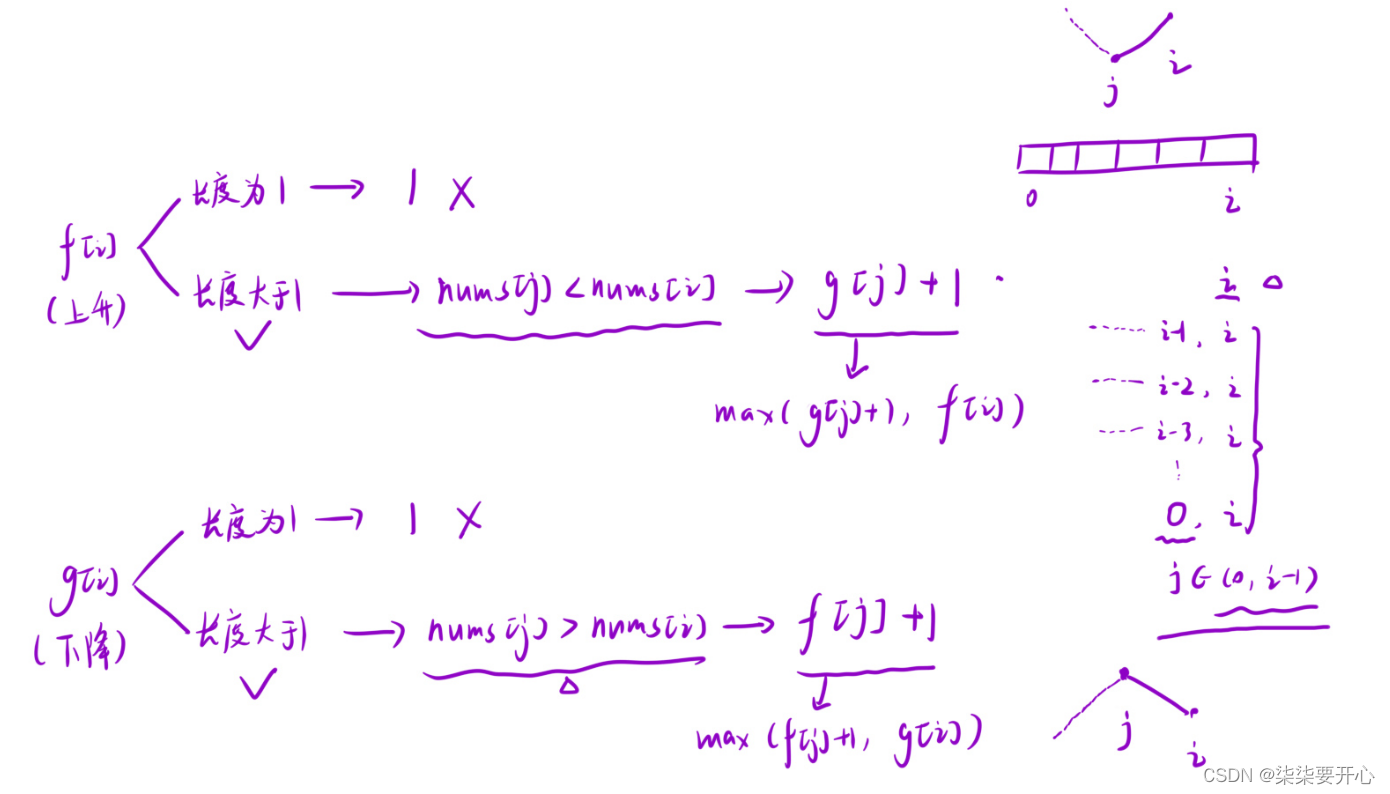
3. 初始化
g表 和 f表全部初始化为 1
4. 填表顺序
从左往右,两个表一起填
5. 返回值
两个表里面的最大值
代码:
class Solution {
public int wiggleMaxLength(int[] nums) {
int n = nums.length;
int[] f = new int[n];
int[] g = new int[n];
for(int i = 0; i < n; i++) {
f[i] = g[i] = 1;
}
int ret = 1;
for(int i = 1; i < n; i++) {
for(int j = 0; j < i; j++) {
if(nums[i] < nums[j]) {
g[i] = Math.max(f[j] + 1, g[i]);
}else if(nums[i] > nums[j]) {
f[i] = Math.max(g[j] + 1, f[i]);
}
}
ret = Math.max(f[i], g[i]);
}
return ret;
}
}
4. 二叉树剪枝
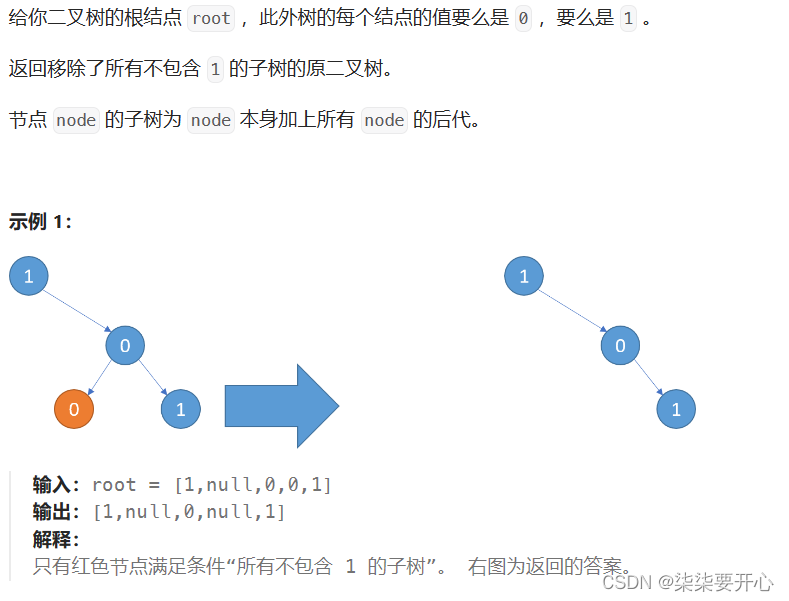
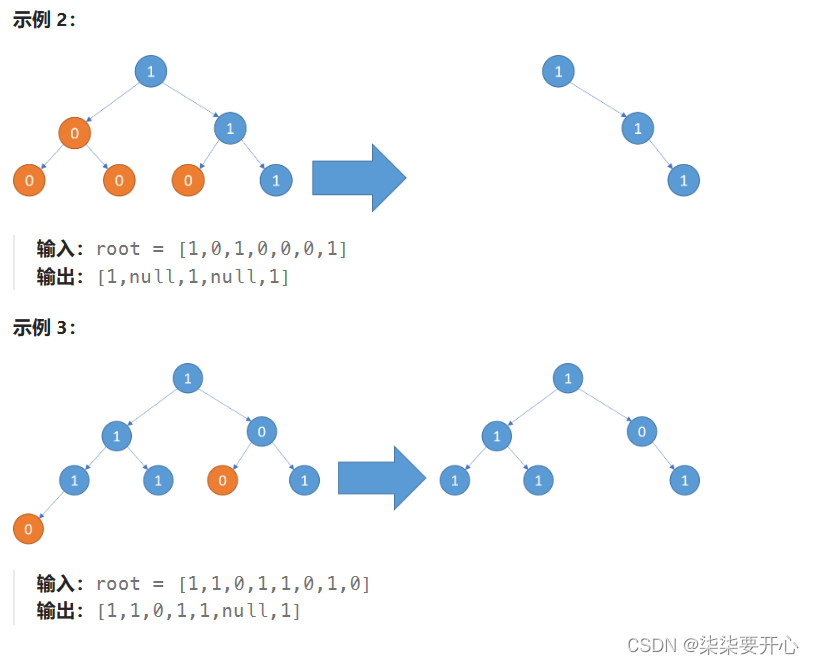
原题链接
题干:
给你二叉树的根结点 root ,此外树的每个结点的值要么是 0 ,要么是 1 。
返回移除了所有不包含 1 的子树的原二叉树。
算法原理:
通过决策树,抽象出递归的三个核心问题
并采用 后序遍历
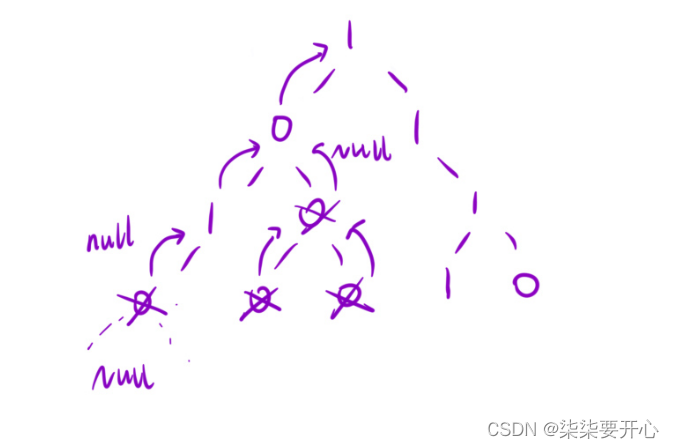
- 函数头
Node * dfs(root) - 函数体
处理左子树
处理右子树
判断 - 递归出口
root == null
代码:
public TreeNode pruneTree(TreeNode root) {
if(root == null) {
return null;
}
root.left = pruneTree(root.left);
root.right = pruneTree(root.right);
if(root.left == null && root.right == null && root.val == 0) {
root = null;
}
return root;
}
5. 验证二叉搜索树
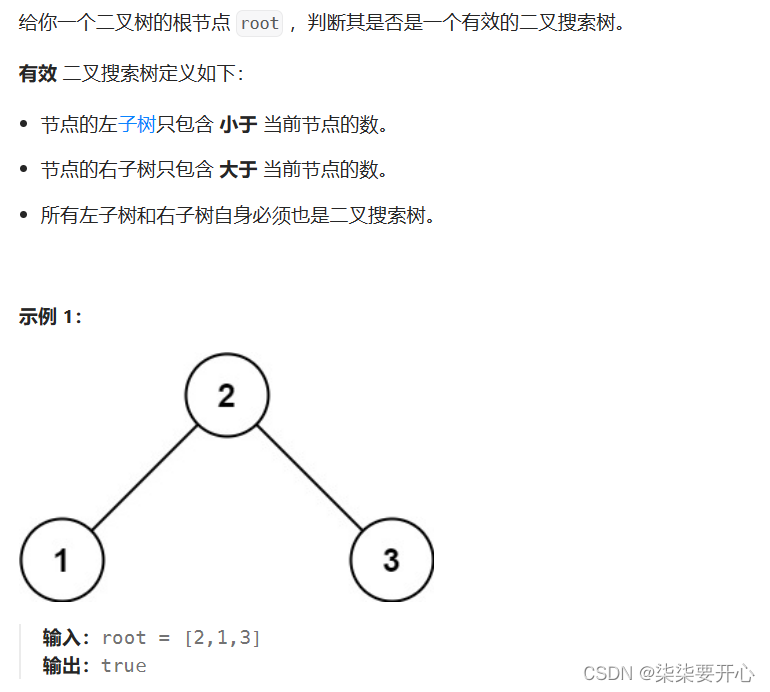
原题链接
题干:
给你一个二叉树的根节点 root ,判断其是否是一个有效的二叉搜索树
算法原理:
我们先要知道一个原理,二叉搜索树的中序遍历的结果,是一个有序的序列
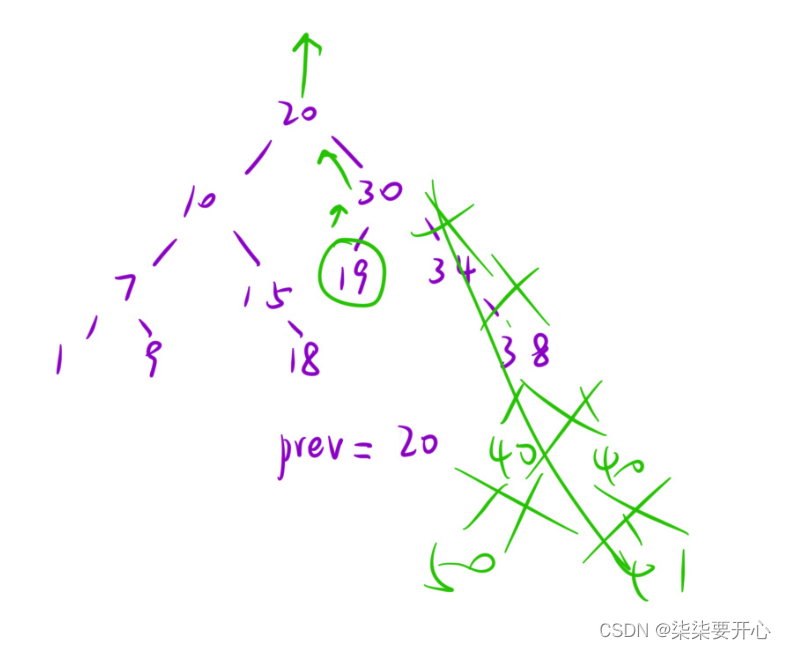
- 使用全局变量
我们可以使用全局变量来记录值,如果不是有序,就可以直接返回 false - 回溯
我们可以知道基本上递归都会有回溯 - 剪枝
剪枝可以加快搜索树
策略一:
左子树是二叉搜索树
当前节点符合二叉搜索树的定义
右子树也是二叉搜索树
策略二:
剪枝
代码:
class Solution {
long prev = Long.MIN_VALUE;
public boolean isValidBST(TreeNode root) {
if(root == null) {
return true;
}
boolean left = isValidBST(root.left);
//剪枝
if(left == false) {
return false;
}
boolean cur = false;
//剪枝
if(root.val > prev) {
cur = true;
}
if(left == false) {
return false;
}
prev = root.val;
boolean right = isValidBST(root.right);
return left && cur && right;
}
}