目录
1、导数和微分
1.1 定义函数:
1.2 趋近过程:
1.3 绘图表示:
2、偏导数
3、梯度
4、链式法则
5、学习心得
在2500年前,古希腊人把一个多边形分成三角形,并把它们的面积相加,才找到计算多边形面积的方法。为 了求出曲线形状(比如圆)的面积,古希腊人在这样的形状上刻内接多边形。如图下所示,内接多边形的 等长边越多,就越接近圆。这个过程也被称为逼近法。
事实上,逼近法就是积分的起源。 2000多年后,微积分的另一支,微分被发明出来。 在微分学最重要的应用是优化问题,即考虑如何把事情做到最好,这种问题在深度学习中是无处不在的。
在深度学习中,我们“训练”模型,不断更新它们,使它们在看到越来越多的数据时变得越来越好。通常情 况下,变得更好意味着最小化一个损失函数(loss function),即一个衡量“模型有多糟糕”这个问题的分数。 最终,我们真正关心的是生成一个模型,它能够在从未见过的数据上表现良好。但“训练”模型只能将模型 与我们实际能看到的数据相拟合。因此,我们可以将拟合模型的任务分解为两个关键问题:
- 优化(optimization):用模型拟合观测数据的过程;
- 泛化(generalization):数学原理和实践者的智慧,能够指导我们生成出有效性超出用于训练的数据集本身的模型。
1、导数和微分
假设我们有一个函数f : R → R,其输入和输出都是标量。如果f的导数存在,这个极限被定义为
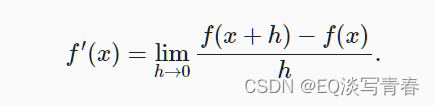
如果f ′ (a)存在,则称f在a处是可微的。如果f在一个区间内的每个数上都是可微的,则此函数在此区间中是可微的。
1.1 定义函数:
为了更好地解释导数,让我们做一个实验。定义 u = f(x) = 3 − 4x 如下:
%matplotlib inline
import numpy as np
from matplotlib_inline import backend_inline
from d2l import torch as d2l
def f(x):
return 3 * x ** 2 - 4 * x1.2 趋近过程:
通过令x = 1并让h接近0,(2.4.1)中(f(x+h)−f(x)) /h 的数值结果接近2。虽然这个实验不是一个数学证明,但稍后 会看到,当x = 1时,导数u ′是2。
def numerical_lim(f, x, h):
return (f(x + h) - f(x)) / h
h = 0.1
for i in range(5):
print(f'h={h:.5f}, numerical limit={numerical_lim(f, 1, h):.5f}')
h *= 0.1输出:
h=0.10000, numerical limit=2.30000
h=0.01000, numerical limit=2.0300
h=0.00100, numerical limit=2.00300
h=0.00010, numerical limit=2.00030
h=0.00001, numerical limit=2.00003
1.3 绘图表示:
现在我们可以绘制函数u = f(x)及其在x = 1处的切线 y = 2x − 3,其中系数2是切线的斜率。
import matplotlib.pyplot as plt
import numpy as np
from matplotlib_inline import backend_inline
from d2l import torch as d2l
def f(x):
return 3 * x ** 2 - 4 * x
def numerical_lim(f, x, h):
return (f(x + h) - f(x)) / h
h = 0.1
for i in range(5):
print(f'h={h:.5f}, numerical limit={numerical_lim(f, 1, h):.5f}')
h *= 0.1
def use_svg_display(): # @save
"""使用svg格式在Jupyter中显示绘图"""
backend_inline.set_matplotlib_formats('svg')
def set_figsize(figsize=(3.5, 2.5)): # @save
"""设置matplotlib的图表大小"""
use_svg_display()
d2l.plt.rcParams['figure.figsize'] = figsize
# @save
def set_axes(axes, xlabel, ylabel, xlim, ylim, xscale, yscale, legend):
"""设置matplotlib的轴"""
axes.set_xlabel(xlabel)
axes.set_ylabel(ylabel)
axes.set_xscale(xscale)
axes.set_yscale(yscale)
axes.set_xlim(xlim)
axes.set_ylim(ylim)
if legend:
axes.legend(legend)
axes.grid()
# @save
def plot(X, Y=None, xlabel=None, ylabel=None, legend=None, xlim=None,ylim=None, xscale='linear', yscale='linear',fmts=('-', 'm--', 'g-.', 'r:'), figsize=(3.5, 2.5), axes=None):
"""绘制数据点"""
if legend is None:
legend = []
set_figsize(figsize)
axes = axes if axes else d2l.plt.gca()
# 如果X有一个轴,输出True
def has_one_axis(X):
return (hasattr(X, "ndim") and X.ndim == 1 or isinstance(X, list)
and not hasattr(X[0], "__len__"))
if has_one_axis(X):
X = [X]
if Y is None:
X, Y = [[]] * len(X), X
elif has_one_axis(Y):
Y = [Y]
if len(X) != len(Y):
X = X * len(Y)
axes.cla()
for x, y, fmt in zip(X, Y, fmts):
if len(x):
axes.plot(x, y, fmt)
else:
axes.plot(y, fmt)
set_axes(axes, xlabel, ylabel, xlim, ylim, xscale, yscale, legend)
x = np.arange(0, 3, 0.1)
plot(x, [f(x), 2 * x - 3], 'x', 'f(x)', legend=['f(x)', 'Tangent line (x=1)'])
plt.show()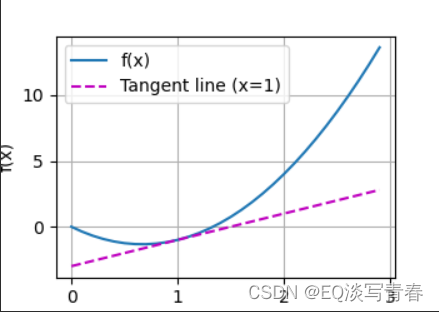
2、偏导数
在深度学习中,函数通常依赖于许多变量。因此,我 们需要将微分的思想推广到多元函数上。
设y = f(x1, x2, . . . , xn)是一个具有n个变量的函数。y关于第i个参数xi的偏导数为:
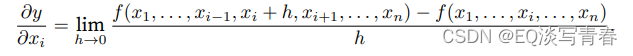
3、梯度
我们可以连结一个多元函数对其所有变量的偏导数,以得到该函数的梯度(gradient)向量。具体而言,设 函数f : R n → R的输入是一个n维向量x = [x1, x2, . . . , xn] ⊤,并且输出是一个标量。函数f(x)相对于x的梯度 是一个包含n个偏导数的向量:

4、链式法则
然而,上面方法可能很难找到梯度。这是因为在深度学习中,多元函数通常是复合的,所以难以应用上述任何规则来微分这些函数。幸运的是,链式法则可以被用来微分复合函数。 让我们先考虑单变量函数。假设函数y = f(u)和u = g(x)都是可微的,根据链式法则:
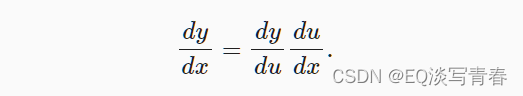
5、学习心得
- 微分和积分是微积分的两个分支,前者可以应用于深度学习中的优化问题。
- 导数可以被解释为函数相对于其变量的瞬时变化率,它也是函数曲线的切线的斜率。
- 梯度是一个向量,其分量是多变量函数相对于其所有变量的偏导数。
- 链式法则可以用来微分复合函数。