备战2024年蓝桥杯 -- 每日一题
Python大学A组

        试题一：奶酪
        试题二：合并集合
        试题三：连通块中点的数量
        试题四：网络分析

---

试题一：奶酪

【题目描述】

        现有一块大奶酪，它的高度为 hℎ，它的长度和宽度我们可以认为是无限大的，奶酪中间有许多半径相同的球形空洞。我们可以在这块奶酪中建立空间坐标系，在坐标系中，奶酪的下表面为 z=0，奶酪的上表面为 z=h。 现在，奶酪的下表面有一只小老鼠 Jerry，它知道奶酪中所有空洞的球心所在的坐标如果两个空洞相切或是相交，则 Jerry 可以从其中一个空洞跑到另一个空洞，特别地，如果一个空洞与下表面相切或是相交，Jerry 则可以从奶酪下表面跑进空洞；如果一个空洞与上表面相切或是相交，Jerry 则可以从空洞跑到奶酪上表面。

        位于奶酪下表面的 Jerry 想知道，在不破坏奶酪的情况下，能否利用已有的空洞跑到奶酪的上表面去? 

        空间内两点 P1(x1,y1,z1)、P2(x2,y2,z2)的距离公式如下：

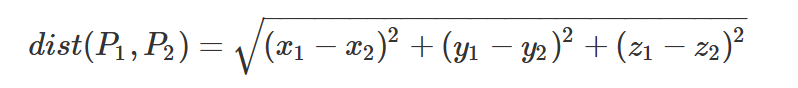
【输入格式】

        每个输入文件包含多组数据。  

        输入文件的第一行，包含一个正整数 T，代表该输入文件中所含的数据组数。  

        接下来是 T 组数据，每组数据的格式如下：

        第一行包含三个正整数 n，h，ℎ 和 r，两个数之间以一个空格分开，分别代表奶酪中空洞的数量，奶酪的高度和空洞的半径。  

        接下来的 n 行，每行包含三个整数 x、y、z，两个数之间以一个空格分开，表示空洞球心坐标为 (x,y,z)。

【输出格式】

        输出文件包含 T行，分别对应 T组数据的答案，如果在第 i 组数据中，Jerry 能从下表面跑到上表面，则输出 Yes，如果不能，则输出 No。

【数据范围】

        1≤n≤1000,
        1≤h,r≤10⁹,
        T≤20,

【输入样例】

3 
2 4 1 
0 0 1 
0 0 3 
2 5 1 
0 0 1 
0 0 4 
2 5 2 
0 0 2 
2 0 4

【输出样例】

Yes
No
Yes

【解题思路】

        首先找到所有的与底面和顶面相交或相切的点，然后两层循环遍历，如果两个球相交或相切也就是两个求联通，则合并一下。处理完成后，枚举每一个与地面相交或相切的点与顶点，如果二者有相同的父节点说明上下联通。

【Python程序代码】

from collections import *
T = int(input())
def find(x):
    if p[x]!=x:p[x] = find(p[x])
    return p[x]

def dist(x1,y1,z1,x2,y2,z2):
    return ( (x2-x1)**2 + (y2-y1)**2 + (z2-z1)**2 )**0.5
for _ in range(T):
    n,h,r = map(int,input().split())
    p = [i for i in range(n+5)]
    a = [[0,0,0]]
    s1,s2 = [0],[0]
    for i in range(n):
        x,y,z = map(int,input().split())
        a.append([x,y,z])
        if z-r<=0:s1.append(i+1)
        if z+r>=h:s2.append(i+1)
    if not len(s1) or not len(s2):
        print('No')
        continue
    for i in range(1,n+1):
        for j in range(i+1,n+1):
            if find(i)==find(j):continue
            d = dist(a[i][0],a[i][1],a[i][2],a[j][0],a[j][1],a[j][2])
            if d<=2*r:
                p[ find(i) ] = find(j)
    f = 0
    for i in range(1,len(s1)):
        if f:break
        for j in range(1,len(s2)):
            if find( s1[i] ) == find(s2[j]):
                f=1; print('Yes')
                break
    if not f:print('No')

---

试题二：合并集合

【题目描述】

一共有 n 个数，编号是 1∼n，最开始每个数各自在一个集合中。

现在要进行 m 个操作，操作共有两种：

1. M a b，将编号为 a 和 b 的两个数所在的集合合并，如果两个数已经在同一个集合中，则忽略这个操作；
2. Q a b，询问编号为 a 和 b 的两个数是否在同一个集合中；

【输入格式】

        第一行输入整数 n 和 m。

        接下来 m 行，每行包含一个操作指令，指令为 M a b 或 Q a b 中的一种。

【输出格式】

        对于每个询问指令 Q a b，都要输出一个结果，如果 a� 和 b� 在同一集合内，则输出 Yes，否则输出 No。

        每个结果占一行。

【数据范围】

        1≤n,m≤105

【输入样例】

4 5
M 1 2
M 3 4
Q 1 2
Q 1 3
Q 3 4

【输出样例】

Yes
No
Yes

【解题思路】

        模板题，不过Python好像过不了？

【Python程序代码】

import sys
imput = sys.stdin.readline
n,m = map(int,input().split())
p = [i for i in range(n+5)]
def find(x):
    if p[x]!=x:p[x] = find(p[x])
    return p[x]
for i in range(m):
    s = list(input().split())
    a,b = int(s[1]),int(s[2])
    if s[0]=='M':
        if find(a)==find(b):continue
        else: p[find(a)]=find(b)
    else:
        if find(a)==find(b):print('Yes')
        else: print('No')

---

试题三：连通块中点的数量

【题目描述】

        给定一个包含 n 个点（编号为 1∼n）的无向图，初始时图中没有边。现在要进行 m 个操作，操作共有三种：

1. C a b，在点 a 和点 b 之间连一条边，a 和 b 可能相等；
2. Q1 a b，询问点 a 和点 b 是否在同一个连通块中，a 和 b 可能相等；
3. Q2 a，询问点 a 所在连通块中点的数量；

【输入格式】

        第一行输入整数 n 和 m 。

        接下来 m 行，每行包含一个操作指令，指令为 C a b，Q1 a b 或 Q2 a 中的一种。

【输出格式】

        对于每个询问指令 Q1 a b，如果 a 和 b 在同一个连通块中，则输出 Yes，否则输出 No。

        对于每个询问指令 Q2 a，输出一个整数表示点 a 所在连通块中点的数量

        每个结果占一行。

【数据范围】

        1≤n,m≤10⁵

【输入样例】

5 5
C 1 2
Q1 1 2
Q2 1
C 2 5
Q2 5

【输出样例】

Yes
2
3

【解题思路】

        在原来并查集的合并基础上加上一个点的数量合并就ok。

【Python程序代码】

n,m = map(int,input().split())
p = [i for i in range(n+5)]
size1 = [1 for i in range(n+5)]
def find(x):
    if p[x]!=x:p[x]=find(p[x])
    return p[x]
def merge(a,b):
    x,y = find(a),find(b)
    p[x] = y
    size1[y] += size1[x]
for i in range(m):
    s = list(input().split())
    if s[0]=='C':
        if s[1]==s[2]:continue
        if find(int(s[1])) == find( int(s[2]) ):continue
        merge(int(s[1]),int(s[2]))
    if s[0]=='Q1':
        if find(int(s[1])) == find( int(s[2]) ):
            print('Yes')
        else:
            print('No')
    if s[0]=='Q2':
        print( size1[find( int(s[1]) )] )

---

试题四：网络分析

【题目描述】

        小明正在做一个网络实验。他设置了 n 台电脑，称为节点，用于收发和存储数据。初始时，所有节点都是独立的，不存在任何连接。小明可以通过网线将两个节点连接起来，连接后两个节点就可以互相通信了。两个节点如果存在网线连接，称为相邻。小明有时会测试当时的网络，他会在某个节点发送一条信息，信息会发送到每个相邻的节点，之后这些节点又会转发到自己相邻的节点，直到所有直接或间接相邻的节点都收到了信息。所有发送和接收的节点都会将信息存储下来。一条信息只存储一次。给出小明连接和测试的过程，请计算出每个节点存储信息的大小。

【输入格式】

        输入的第一行包含两个整数 n,m，分别表示节点数量和操作数量。节点从 1 至 n 编号。接下来 m 行，每行三个整数，表示一个操作。

• 如果操作为 1 a b，表示将节点 a 和节点 b 通过网线连接起来。当 a = b 时，表示连接了一个自环，对网络没有实质影响。
• 如果操作为 2 p t，表示在节点 p 上发送一条大小为 t 的信息。

【输出格式】

        输出一行，包含 n 个整数，相邻整数之间用一个空格分割，依次表示进行完上述操作后节点 1 至节点 n 上存储信息的大小。

【数据范围】

        1≤n≤10000,
        1≤m≤105,
        1≤t≤100

【输入样例】

4 8
1 1 2
2 1 10
2 3 5
1 4 1
2 2 2
1 1 2
1 2 4
2 2 1

【输出样例】

13 13 5 3

【解题思路】

        思考并查集的树是如何构造出来的，当没有进行路径压缩时，这个点的信息量可以考虑成该点到对应父节点路径上结点的信息量之和，那么两个集合合并时该如何维护结点信息量呢？如果p[a]=b也就是a结点指向b结点，那么对应的d[a] -= d[b]即可。

【Python程序代码】

n,m = map(int,input().split())
p = [i for i in range(n+5)]
size1 = [1 for i in range(n+5)]
def find(x):
    if p[x]!=x:p[x]=find(p[x])
    return p[x]
def merge(a,b):
    x,y = find(a),find(b)
    p[x] = y
    size1[y] += size1[x]
for i in range(m):
    s = list(input().split())
    if s[0]=='C':
        if s[1]==s[2]:continue
        if find(int(s[1])) == find( int(s[2]) ):continue
        merge(int(s[1]),int(s[2]))
    if s[0]=='Q1':
        if find(int(s[1])) == find( int(s[2]) ):
            print('Yes')
        else:
            print('No')
    if s[0]=='Q2':
        print( size1[find( int(s[1]) )] )