思路 1:
我将res[i]定义为:一定要取第 i 个房子的前提下,能获取的最大金额。那么直接用cnt从头记录到尾,每个房子的res最大值即是答案。那么递推公式是什么?res[i]=max(res[i-2],res[i-1],...,res[0])+nums[i]。数组初始化是什么?res[i]=nums[i],也就是只取每个房子的金额。
代码:
C++:
class Solution {
public:
int rob(vector<int>& nums) {
int len=nums.size();
int cnt=0;
vector<int> res(len,0); //以该房子为结尾,偷盗的最大金额
//那如果res[i]定义为截止到房子i为止,能获取的最大金额呢?
//初始化res
for(int i=0;i<len;i++){
res[i]=nums[i];
cnt=max(cnt,res[i]);
}
for(int i=0;i<len;i++){
for(int j=0;j<=i-2;j++){
res[i]=max(res[i],res[j]+nums[i]);
cnt=max(cnt,res[i]);
}
}
return cnt;
}
};Python:
class Solution:
def rob(self, nums: List[int]) -> int:
len_nums=len(nums)
cnt=0
res=[0]*len_nums
for i in range(len_nums):
res[i]=nums[i]
cnt=max(cnt,res[i])
for i in range(len_nums):
for j in range(i-1):
res[i]=max(res[i],res[j]+nums[i])
cnt=max(cnt,res[i])
return cnt那如果res[i]定义为偷前 i 个房子,能获取的最大金额呢?递推公式是什么呢?数组初始化又是什么呢?
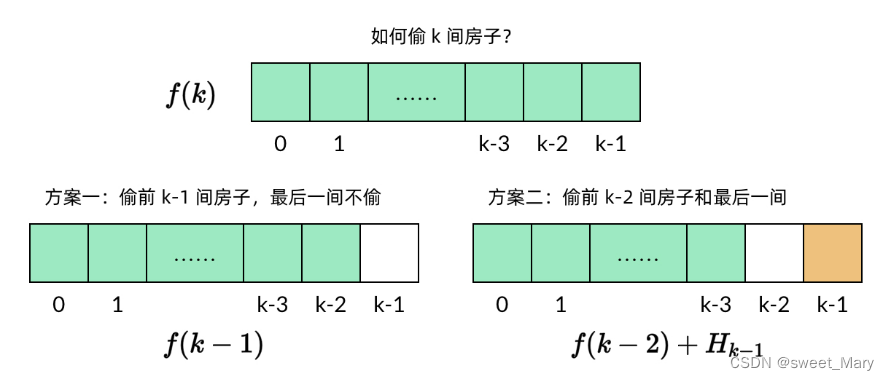
思路2
递推公式为:g[i]=max(g[i-1],g[i-2]+nums[i])
可以看一下标答,还是很清晰的:198. 打家劫舍 - 力扣(LeetCode)
数组初始化:
要考虑len(nums)=1的情况哦,别掉进坑了
g[0]=nums[0],g[1]=max(nums[0],nums[1])
代码:
C++:
class Solution {
public:
int rob(vector<int>& nums) {
int len=nums.size();
if(len==1){return nums[0];}
vector<int> g(len,0);
g[0]=nums[0];
g[1]=max(nums[0],nums[1]);
for(int i=2;i<len;i++){
g[i]=max(g[i-1],g[i-2]+nums[i]);
}
return g[len-1];
}
};Python:
class Solution:
def rob(self, nums: List[int]) -> int:
len_nums=len(nums)
if len_nums==1:
return nums[0]
g=[0]*len_nums
g[0]=nums[0]
g[1]=max(nums[0],nums[1])
for i in range(2,len_nums):
g[i]=max(g[i-1],g[i-2]+nums[i])
return g[len_nums-1]