索引

历年CSP认证考试真题题解总汇持续更新

2021-04-2 邻域均值 经典二维前缀和

这题算是第二题中简单的那种了，但是我还是写了接近40分钟才AC，写二维前缀和不太熟练，并且又出了很多很蠢的错误。

思路

这题一拿到我没看到是均值，然后就想怎么减少重复计算呢？就是滑动窗口时，不断更新，并且用的上一个状态窗口来更新下一个这样就会减少重复计算，但是读题后发现是均值，那不就是要求和吗？所以就想到了二维前缀和，之前也做过二维前缀和的题，所以就开始写了。

遇到的问题

1. 只顾着求和了，忘记除以数量取平均了
2. 忘记用double类型存储除法

在算均值的时候，我想着只要是反正也是大于的数也会判断为等于

            if (matrix_sum / matrix_num <= t)
                num++;

这样就会导致原本大于t的数也被算进等于t的里了，这样就会导致num很大，不符合答案

所以改成

            if (matrix_sum / (double)matrix_num <= t)
                num++;

这样就没有问题了。

3. 忘记处理边界的问题

就是根据题目给的条件里

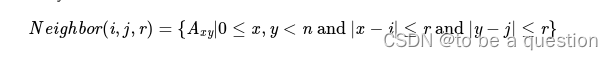
我们不难发现，窗口的大小不是固定的，在边缘的话有可能会少，所以我们要判断边界条件，一开始没有注意到，后来才注意到

int iaddr = min(n, i + r), jaddr = min(n, j + r), isubr = max(0, i - r - 1), jsubr = max(0, j - r - 1);

4. 注意二维前缀和sum[i][j]是包括自己a[i][j]的

所以加上的就是sum[i-r-1][j-r-1]，并且isubr和jsubr的下界是0不是1

然后基本就可以100分了

完整代码

#include <bits/stdc++.h>
using namespace std;
int n, L, r, t;
int a[601][601];
int sum[601][601]; // 二维前缀和数组
int main()
{
    cin >> n >> L >> r >> t;
    for (int i = 1; i <= n; i++)
    {
        for (int j = 1; j <= n; j++)
        {
            cin >> a[i][j];
        }
    }
    for (int i = 1; i <= n; i++)
    {
        for (int j = 1; j <= n; j++)
        {
            sum[i][j] = sum[i][j - 1] + sum[i - 1][j] - sum[i - 1][j - 1] + a[i][j];
        }
    }
    int num = 0;
    for (int i = 1; i <= n; i++)
    {
        for (int j = 1; j <= n; j++)
        {
            int iaddr = min(n, i + r), jaddr = min(n, j + r), isubr = max(0, i - r - 1), jsubr = max(0, j - r - 1);
            int matrix_sum = sum[iaddr][jaddr] - sum[isubr][jaddr] - sum[iaddr][jsubr] + sum[isubr][jsubr];
            int matrix_num = (iaddr - isubr ) * (jaddr - jsubr );
            if (matrix_sum / (double)matrix_num <= t)
                num++;
        }
    }
    cout << num;
    return 0;
}