题目

给定一个整数数组 nums 和一个整数 k ，返回其中元素之和可被 k 整除的（连续、非空） 子数组 的数目。

子数组 是数组的 连续 部分。

示例 1：

输入：nums = [4,5,0,-2,-3,1], k = 5
输出：7
解释：
有 7 个子数组满足其元素之和可被 k = 5 整除：
[4, 5, 0, -2, -3, 1], [5], [5, 0], [5, 0, -2, -3], [0], [0, -2, -3], [-2, -3]

示例 2:

输入: nums = [5], k = 9
输出: 0

算法思路

经典的子数组问题，但仔细分析题目后发现无法使用滑动窗口，因为数组有正有负，其整体不具备单调性，所以只能考虑前缀和的方式来解决，但每加减一位都会引起数据和的增减性是不确定的，而且子数组并不一定是要从开头开始，所以不能完全使用前缀和来解决这个问题。

此时就要引入一个数学思想来将问题进行转化

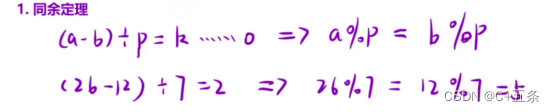
假设如果两个数的差可以被k整除，也就是存在一个p被a和b的差所除后所得的商为k

此时a%p=a%p

证明如下：

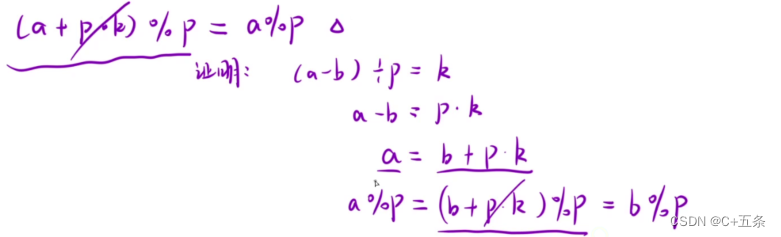
因为数组中有负数的存在，而在C++中负数对正数取模结果依然是负数，而余数为负会干扰我们的判断，所以需要用下列方法将取模后的余数变为正数，此时是不影响取模后的结果的

 

 

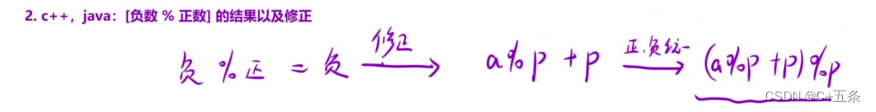
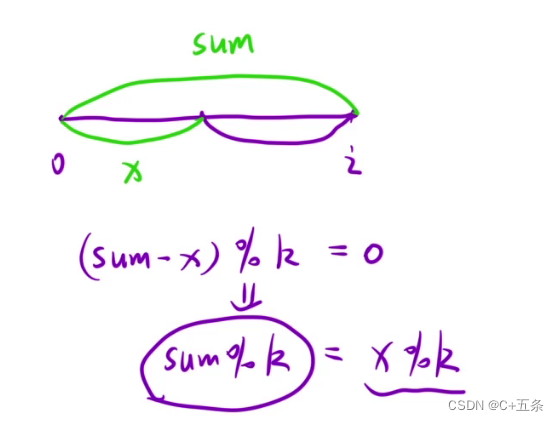
 因为要求子数组，所以问题可以转化为求第i位置之前，以i位置为结尾的有多少个子数组可以被k整除，假设把到i位置划分为两部分，前一部分和为x后一部分和为k的整数倍，那么可以推出公式     求(sum-x)%k=0的情况有多少中，而根据上面的同余定理进而可以转化为求满足i位置之前sum%k=x%k的情况有多少种，又考虑到可能有负数存在，所以需要对取模的值进行修正。

所以问题最终可以转化为：

代码实现

注意：此时不是真的要创建出一个前缀和表，因为只需判断在i之前是否存在满足条件的情况，所以只需在遍历时用哈希表进行记录，每次求和再去哈希表中查找是否有符合的情况即可。

class Solution {
public:
    int subarraysDivByK(vector<int>& nums, int k) 
    {
        map<int,int> hash;
        hash[0]=1;
        int sum=0;
        int ret=0;
        for(auto e:nums)
        {
            sum+=e;
            int r=(sum%k+k)%k;
            if(hash.count(r)) ret+=hash[r];
            hash[r]++;
        }
        return ret;
    }
};