算法练习：前缀和

news2024/10/7 14:28:07

目录

  • 1. 一维前缀和
  • 2. 二维前缀和
  • 3. 寻找数组中心下标
  • 4. 除自身以外数组的乘积
  • 5. !和为k的子数字
  • 6. !和可被k整除的子数组
  • 7. !连续数组
  • @8. 矩阵区域和

1. 一维前缀和

  1. 题目信息：
    在这里插入图片描述
  2. 题目链接：
    一维前缀和
  3. 思路：求前缀和数组，sum = dp[r] - dp[l - 1]
#include <iostream>
#include <vector>
using namespace std;

int main() 
{
    int n = 0;
    int q = 0;
    cin >> n >> q;
    //先求前缀和数组
    int num = 0;
    //计算时可能溢出
    vector<long long> dp;
    dp.push_back(0);
    for(int i = 0; i < n; i++)
    {
        cin >> num;
        dp.push_back(num + dp[i]);
    }

    //求询问区间之和
    //dp[i] - dp[i - 1]
    //计算时可能溢出
    vector<long long> ret;
    int left = 0,right = 0;
    for(int i = 0; i < q; i++)
    {
        cin >> left >> right;
        ret.push_back(dp[right] - dp[left - 1]);
    }

    for(auto e : ret)
    {
        cout << e << endl;
    }

    return 0;    
}

优化：

int main() 
{
    int n = 0;
    int q = 0;
    cin >> n >> q;
    //先求前缀和数组
    int num = 0;
    //默认初始化为0
    vector<int> arr(n + 1);
    for(int i = 1; i < n + 1; i++)
    {
        cin >> num;
        arr[i] = num;
    }

    //防溢出
    vector<long long> dp(n + 1);
    for(int i = 1; i < n + 1; i++)
    {
        dp[i] = dp[i - 1] + arr[i];
    }

    int l = 0, r = 0;
    while(q--)
    {
        cin >> l >> r;
        cout << dp[r] - dp[l - 1] << endl;
    }
    
    return 0;    
}

2. 二维前缀和

  1. 题目信息：
    在这里插入图片描述
  2. 题目链接：
    二维前缀和
  3. 思路：二维前缀和

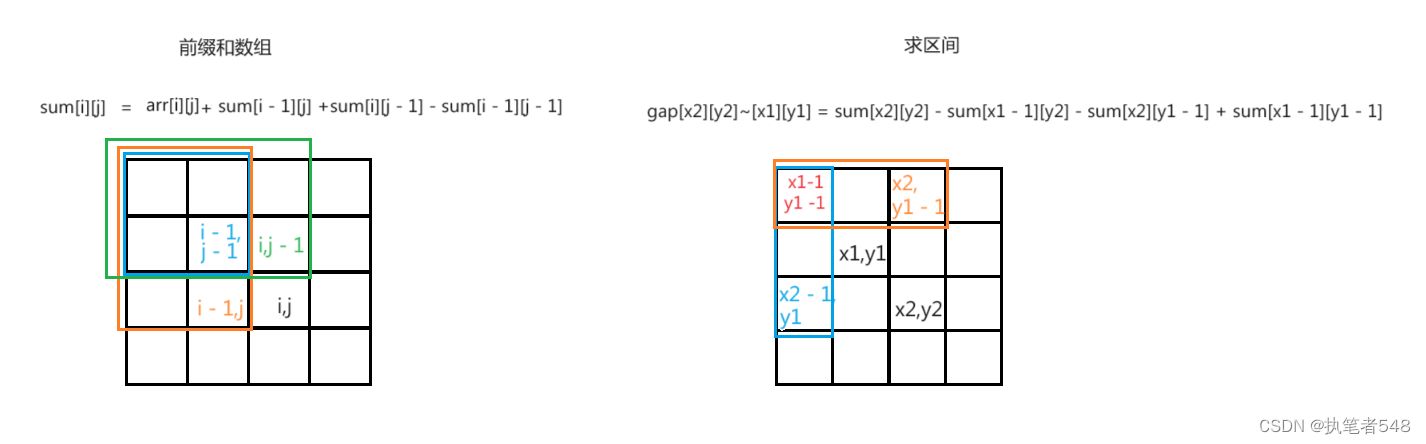
在这里插入图片描述

int main()
{
    int n = 0, m = 0, q = 0;
    //先遍历，得值    
    cin >> n >> m >> q;
    vector<vector<long long>> arr;
    vector<long long> part(m + 1);
    for (int i = 0; i < n + 1; i++)
    {
        arr.push_back(part);
    }

    vector<vector<long long>> dp(arr);

    for (int i = 1; i <= n; i++)
    {
        for (int j = 1; j <= m; j++)
        {
            cin >> arr[i][j];
        }
    }

    //求前缀和数组
    for (int i = 1; i <= n; i++)
    {
        for (int j = 1; j <= m; j++)
        {
            dp[i][j] = arr[i][j] + dp[i - 1][j] + dp[i][j - 1] - dp[i - 1][j - 1];
        }
    }

    //求区间值
    //x1,y1小，x2,y2大
    int x1, x2, y1, y2 = 0;
    while (q--)
    {
        cin >> x1 >> y1 >> x2 >> y2;
        cout << dp[x2][y2] - dp[x1 - 1][y2] - dp[x2][y1 - 1] + dp[x1 - 1][y1 - 1] << endl;

    }

    return 0;
}

3. 寻找数组中心下标

  1. 题目信息：
    在这里插入图片描述
  2. 题目链接：
    寻找数组的中心下标
  3. 思路：正向与逆向前缀和数组，边界处理，特殊情况处理
class Solution
{
public:
    int pivotIndex(vector<int>& nums)
    {
        int n = nums.size();
        vector<int> dp1(n);
        vector<int> dp2(n);
        //空
        if(nums.size() == 1)
        {
            return 0;
        }

        int left = 0, right = nums.size() - 1;
        //求前缀和数组
        //顺序
        while (left < nums.size())
        {
            if (left > 0)
            {
                dp1[left] = nums[left] + dp1[left - 1];
            }
            else
            {
                dp1[left] = nums[left];
            }
            left++;
        }
        //倒序
        while (right >= 0)
        {
            if (right < nums.size() - 1)
            {
                dp2[right] = nums[right] + dp2[right + 1];
            }
            else
            {
                dp2[right] = nums[right];
            }
            right--;
        }


        //遍历求中间结点
        for (int cur = 0; cur < nums.size(); cur++)
        {
            //dp1顺序
            //dp2倒序
            if (cur == 0)
            {
                if (dp2[cur + 1] == 0)
                {
                    return cur;
                }
            }
            else if (cur == nums.size() - 1)
            {
                if (dp1[cur - 1] == 0)
                {
                    return cur;
                }
            }
            else
            {
                if (dp1[cur - 1] == dp2[cur + 1])
                {
                    return cur;
                }
            }
        }

        return -1;
    }
};

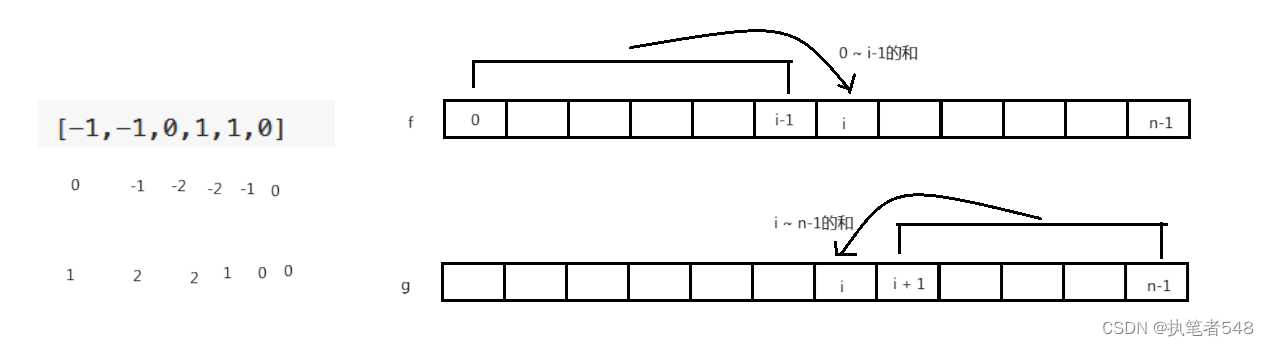
优化：
在这里插入图片描述

class Solution 
{
public:
    int pivotIndex(vector<int>& nums) 
    {
        int n = nums.size();
        //顺序
        vector<int> f(n);
        //逆序
        vector<int> g(n);

        //边界问题特殊处理
        f[0] = 0;
        //f[i] -> [0, i - 1]
        for(int i = 1; i < n; i++)
        {
            f[i] = nums[i - 1] + f[i - 1];
        }

        g[n - 1] = 0;
        for(int i = n - 2; i >= 0; i--)
        {
            g[i] = g[i + 1] + nums[i + 1];
        }

        for(int i = 0; i < n; i++)
        {
            if(f[i] == g[i])
            {
                return i;
            }
        }

        return -1;
    }
};

4. 除自身以外数组的乘积

  1. 题目信息：
    在这里插入图片描述
  2. 题目链接：
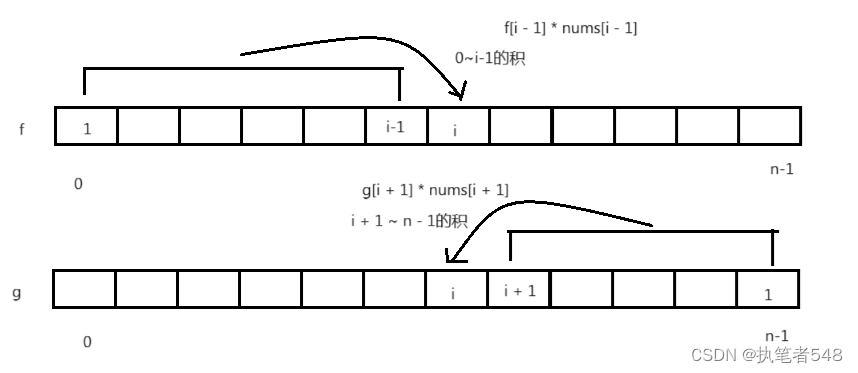
    除自身以外数组的乘积
  3. 思路：前缀 + 后缀数组
class Solution 
{
public:
    vector<int> productExceptSelf(vector<int>& nums) 
    {
        int n = nums.size();
        vector<int> f(n);
        vector<int> g(n);
        f[0] = nums[0];
        for(int i = 1; i < n; i++)
        {
            f[i] = nums[i] * f[i - 1];
        }

        g[n - 1] = nums[n - 1];
        for(int i = n - 2; i >= 0; i--)
        {
            g[i] = nums[i] * g[i + 1];
        }

        vector<int> ret(n);
        for(int i = 0; i < n; i++)
        {
            if(i == 0)
            {
                ret[i] = g[i + 1];
            }
            else if(i == n - 1)
            {
                ret[i] = f[i - 1];
            }
            else
            {
                ret[i] = g[i + 1] * f[i - 1];
            }
        }

        return ret;
    }
};

优化：
在这里插入图片描述

class Solution 
{
public:
    vector<int> productExceptSelf(vector<int>& nums) 
    {
        int n = nums.size();
        vector<int> f(n);
        vector<int> g(n);

        f[0] = 1;
        //顺序
        for(int i = 1; i < n; i++)
        {
            f[i] = f[i - 1] * nums[i - 1];
        }

        g[n - 1] = 1;
        //逆序
        for(int i = n - 2; i >= 0; i--)
        {
            g[i] = g[i + 1] * nums[i + 1];
        }

        vector<int> ret(n);
        for(int i = 0; i < n; i++)
        {
            ret[i] = f[i] * g[i];
        }

        return ret;
    }
};

5. !和为k的子数字

  1. 题目信息：
    在这里插入图片描述
  2. 题目链接：
    和为k的子数组
  3. 思路：前缀和，元素没有单调性，无法使用滑动窗口，逆向求sum - k，可以求得为i为尾的所有数组
class Solution 
{
public:
    int subarraySum(vector<int>& nums, int k) 
    {
        int ret = 0;
        unordered_map<int ,int> hash;
        //sum - k == 0时，即sum就为k
        hash[0] = 1;

        int sum = 0;
        //用哈希表代替遍历
        for(auto e : nums)
        {
            sum += e;
            if(hash.count(sum - k))
            {
                ret += hash[sum - k];
            }
            //插入哈希表
            //可能存在重复前缀和
            hash[sum]++;
        }

        return ret;
    }
};

6. !和可被k整除的子数组

  1. 题目信息：
    在这里插入图片描述
  2. 题目链接：
    和可被k整除的子数组
  3. 思路：前缀和，哈希表，同余定理，C++中负数除以整数的余数修正(num % k + k) % k
class Solution 
{
public:
    int subarraysDivByK(vector<int>& nums, int k) 
    {
        int sum = 0;
        unordered_map<int,int> hash;
        int ret = 0;
        int count = 0;
        //sum % k 本身就符合要求
        hash[0] = 1;
        for(auto e : nums)
        {
            sum += e;
            //(sum1 - sum2) % k == 0
            //同余定理
            //负数除整数的余数
            //哈希表中存余数
            if(hash.count((sum % k + k) % k))
            {
                ret += hash[(sum % k + k) % k];
            }
            hash[(sum % k + k) % k]++;
        }

        return ret;
    }
};

7. !连续数组

  1. 题目信息：
    在这里插入图片描述
  2. 题目链接：
    连续数组
    3.思路：前缀加哈希表，求长度，记录下标
class Solution 
{
public:
    int findMaxLength(vector<int>& nums) 
    {
        for(auto& e : nums)
        {
            if(e == 0)
            {
                e = -1;
            }
        }

        unordered_map<int,int> hash;
        int sum = 0;
        int len = 0;
        //细节，刚好sum为0
        hash[0] = -1;
        for(int i = 0; i < nums.size(); i++)
        {
            //将所有的前缀和与对应下标记录至哈希表中
            sum += nums[i];
            //返回的是长度，最长数组的长度
            if(hash.count(sum) && len < i - hash[sum])
            {
                len = i - hash[sum];
            }
            
            //不存在添加下标
            if(!hash.count(sum))
            {
                hash[sum] = i;
            }
        }

        return len;
    }
};

@8. 矩阵区域和

  1. 题目信息：
    在这里插入图片描述
  2. 题目链接：
    矩阵区域和
  3. 思路：前缀和二维数组，边界问题分析

思路：
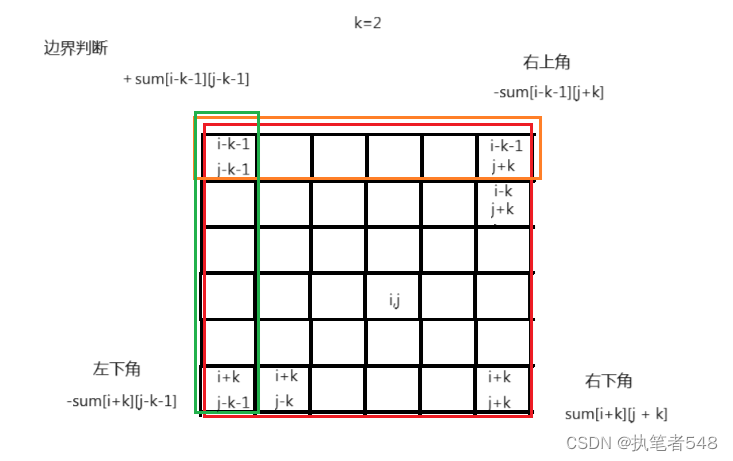
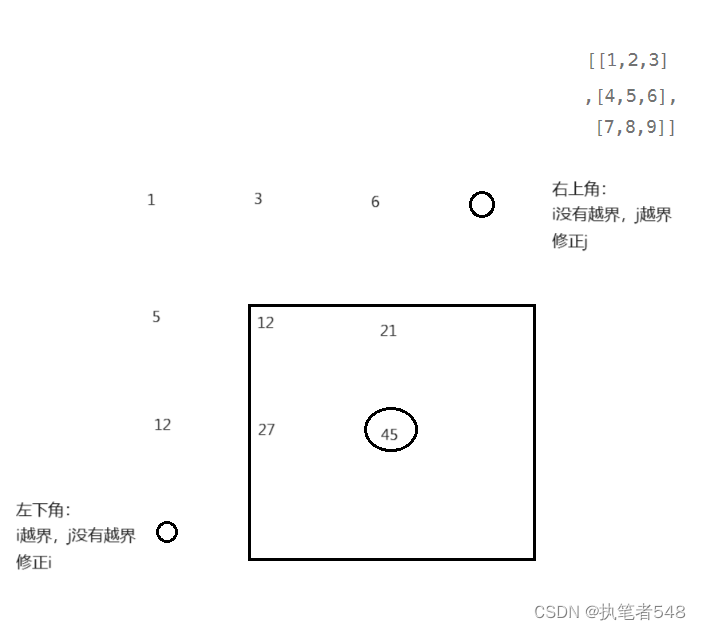
在这里插入图片描述
边界问题：
在这里插入图片描述

class Solution 
{
public:
    vector<vector<int>> matrixBlockSum(vector<vector<int>>& mat, int k)
    {
        vector<int> part1(mat[0].size(), 0);
        vector<vector<int>> answer(mat.size(), part1);
        vector<int> part2(mat[0].size() + 1, 0);
        vector<vector<int>> dp(mat.size() + 1, part2);
        //二维数组的前缀和
        for (int i = 1; i < dp.size(); i++)
        {
            for (int j = 1; j < dp[0].size(); j++)
            {
                dp[i][j] = dp[i - 1][j] + dp[i][j - 1] - dp[i - 1][j - 1] + mat[i - 1][j - 1];
            }
        }

        for (int i = 0; i < mat.size(); i++)
        {
            for (int j = 0; j < mat[0].size(); j++)
            {
                int sum = 0;
                //右下角
                //边界情况，修正
                int pos1 = i + k + 1;
                int pos2 = j + k + 1;
                if (pos1 >= dp.size())
                {
                    pos1 = dp.size() - 1;
                }

                if (pos2 >= dp[0].size())
                {
                    pos2 = dp[0].size() - 1;
                }
                sum += dp[pos1][pos2];

                //右上角
                pos1 = i - k;
                pos2 = j + k + 1;
                //i符合，j不符合
                if (pos1 >= 1 && pos2 >= dp[0].size())
                {
                    pos2 = dp[0].size() - 1;
                }

                if (pos1 >= 1 && pos2 < dp[0].size())
                {
                    sum -= dp[pos1][pos2];
                }

                //左下角
                pos1 = i + k + 1;
                pos2 = j - k;
                //i不符合，j符合
                if (pos1 >= dp.size() && pos2 >= 1)
                {
                    pos1 = dp.size() - 1;
                }

                if (pos1 < dp.size() && pos2 >= 1)
                {
                    sum -= dp[pos1][pos2];
                }

                //左上角
                if (i - k >= 1 && j - k >= 1)
                {
                    sum += dp[i - k][j - k];
                }

                answer[i][j] = sum;
            }
        }

        return answer;
    }
};

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1525571.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

预应力锚杆测力计安装埋设

预应力锚杆测力计安装埋设

锚杆测力计用于观测预应力锚杆预应力的形成与变化。当前&#xff0c;预应力锚杆广泛地应用于岩土工程的锚固结构中&#xff0c;通过安装测力计观测锚杆&#xff0c;可以了解锚固力的形成与变化&#xff0c;从而保证监测工程的质量与安全。测力计的安装包括安装测力计和观测锚杆…
阅读更多...
【LeetCode热题100】 226. 翻转二叉树（二叉树）

【LeetCode热题100】 226. 翻转二叉树（二叉树）

一.题目要求 给你一棵二叉树的根节点 root &#xff0c;翻转这棵二叉树&#xff0c;并返回其根节点。 二.题目难度 简单 三.输入样例 示例 1&#xff1a; 输入&#xff1a;root [4,2,7,1,3,6,9] 输出&#xff1a;[4,7,2,9,6,3,1] 示例 2&#xff1a; 输入&#xff1a;…
阅读更多...
餐饮店引流活动方案与最佳营销方案揭秘

餐饮店引流活动方案与最佳营销方案揭秘

想开实体店或正在创业的朋友们&#xff0c;大家好&#xff01;我是一名资深的实体店创业者&#xff0c;本人经营鲜奶吧5年时间&#xff0c;做的是社区店&#xff0c;今天我将分享一些餐饮店引流活动和营销方案的干货&#xff0c;希望能给大家带来一些启发和帮助。 一、引流活动…
阅读更多...
【人工智能】英文学习材料02（每日一句）

【人工智能】英文学习材料02（每日一句）

&#x1f33b;个人主页&#xff1a;相洋同学 &#x1f947;学习在于行动、总结和坚持&#xff0c;共勉&#xff01; 目录 Supervised Learning&#xff08;监督学习&#xff09; Unsupervised Learning&#xff08;无监督学习 &#xff09; Semi-supervised Learning&#…
阅读更多...
【视频图像取证篇】模糊图像增强技术之色彩空间类滤波器场景应用小结

【视频图像取证篇】模糊图像增强技术之色彩空间类滤波器场景应用小结

【视频图像取证篇】模糊图像增强技术之色彩空间类滤波器场景应用小结 模糊图像增强技术之色彩空间HSI滤波器—【蘇小沐】 &#xff08;一&#xff09;色彩空间滤波器 1、HSI滤波器 HSI&#xff08;色调、饱和度和强度&#xff09;滤镜用于将彩色图像转换为 HSI 图像。这意味…
阅读更多...
当贝X5 Ultra坚果N1S Ultra哪个好？2024年旗舰投影仪哪家强

当贝X5 Ultra坚果N1S Ultra哪个好？2024年旗舰投影仪哪家强

家用投影仪在目前年轻用户新家装修的娱乐选择上&#xff0c;有着越来越大的占比。不过虽然投影仪的体验已经逐渐弯道超越传统电视&#xff0c;画面和沉浸感已经抹去了曾经的一些小问题&#xff1b;但仍然有很多雷区和选购的迷惑&#xff0c;以致于在同价位往往陷入不知道哪款更…
阅读更多...
展厅设计提高人气的妙招

展厅设计提高人气的妙招

1、清晰的标识 展厅门口的标识是消费者第一眼能了解到的信息&#xff0c;所以一定要做到简单清楚&#xff0c;在开设专卖店时&#xff0c;就要将标识做到清晰醒目&#xff0c;方便客户寻找。 2、舒适的灯光 灯光是展厅装修中最为重要的一部分&#xff0c;灯光太亮会让人感觉不舒…
阅读更多...
基于spring boot的钢材销售管理系统的设计与实现

基于spring boot的钢材销售管理系统的设计与实现

钢材销售管理系统 摘 要 本系统为用户而设计制作钢材销售管理系统&#xff0c;旨在实现钢材销售智能化、现代化管理。本钢材销售管理自动化系统的开发和研制的最终目的是将钢材销售的运作模式从手工记录数据转变为网络信息查询管理&#xff0c;从而为现代管理人员的使用提供更…
阅读更多...
【Docker】使用Docker部署IT运维管理平台CAT

【Docker】使用Docker部署IT运维管理平台CAT

作者怀揣着一个美好的愿景&#xff0c;旨在提升管理效率、推动开源项目的蓬勃发展。 来一杯咖啡与茶&#xff0c;为 IT 运维从业者减轻管理负担&#xff0c;提升管理效率&#xff0c;从繁重无序的工作中解压出来&#xff0c;利用剩余时间多喝一杯休息一下。 这是一个专为 IT 运…
阅读更多...
亮点抢先看！4月16-17日，百度Create大会开设“AI公开课”，大咖带你打造赚钱工具

亮点抢先看！4月16-17日，百度Create大会开设“AI公开课”，大咖带你打造赚钱工具

3月16日&#xff0c;2024百度Create AI开发者大会正式开放售票&#xff0c;嘉宾套票定价399元。据悉&#xff0c;本次大会以“创造未来&#xff08;Create the Future&#xff09;”为主题&#xff0c;设有20深度论坛、超30节AI公开课、3000平AI互动体验区和AI音乐节等精彩环节…
阅读更多...
AJAX-Promise

AJAX-Promise

Promise 基本使用 定义&#xff1a;Promise对象用于表示一个异步操作的最终完成&#xff08;或失败&#xff09;及其结果值 好处&#xff1a; 1.逻辑更清晰 2.了解axios函数内部运作机制 3.能解决回调函数的问题 // 1.创建Promise对象 const p new Promise((resolve,reject…
阅读更多...
【Web】浅聊Hessian反序列化之Resin的打法——远程类加载

【Web】浅聊Hessian反序列化之Resin的打法——远程类加载

目录 前言 原理分析 XString&#xff1a;触发恶意类toString QName的设计理念&#xff1f; 远程恶意类加载Context&#xff1a;ContinuationContext QName&#xff1a;恶意toString利用 hash相等构造 EXP 前言 精神状态有点糟糕&#xff0c;随便学一下吧 首先明确一个…
阅读更多...
现代化的轻量级Redis桌面客户端Tiny RDM

现代化的轻量级Redis桌面客户端Tiny RDM

​欢迎光临我的博客查看最新文章: https://river106.cn 1、简介 Tiny RDM&#xff08;全称&#xff1a;Tiny Redis Desktop Manager&#xff09;是一个界面现代化的轻量级Redis桌面客户端&#xff0c;支持Linux、Mac和Windows。它专为开发和运维人员设计&#xff0c;使得与Red…
阅读更多...
2.shell中的echo命令

2.shell中的echo命令

目录 概述实践shell结果 结束 概述 echo 命令详解 实践 shell #!/bin/bash # 输出一些变量或打印一些字符串 # 加双引号&#xff0c;空格是会保留的 echo "hello , world" # 不加&#xff0c;不会保留 echo hello , worldvar11 "a b c d&…
阅读更多...
基于spring boot实现接口管理平台

基于spring boot实现接口管理平台

数据库结构 /* Navicat MySQL Data TransferSource Server : localhost_3306 Source Server Version : 50724 Source Host : localhost:3306 Source Database : interfaceTarget Server Type : MYSQL Target Server Version : 50724 File Encoding…
阅读更多...
Java毕业设计-基于SpringBoot的CSGO赛事管理系统-毕业论文+答辩PPT（附源代码+演示视频）

Java毕业设计-基于SpringBoot的CSGO赛事管理系统-毕业论文+答辩PPT（附源代码+演示视频）

文章目录 前言一、毕设成果演示&#xff08;源代码在文末&#xff09;二、毕设摘要展示1、开发说明2、需求分析3、系统功能结构 三、系统实现展示1、系统功能模块2、管理员功能模块3、参赛战队功能模块4、合作方功能模块 四、毕设内容和源代码获取总结 Java毕业设计-基于Spring…
阅读更多...
Java代码基础算法练习-判断素数-2024.03.17

Java代码基础算法练习-判断素数-2024.03.17

任务描述&#xff1a; 输入一个数x&#xff0c;判断它是否是素数。 提示&#xff1a;素数是只能被1和它本身整除的数&#xff0c;1不是素数。 任务要求&#xff1a; 代码示例&#xff1a; package march0317_0331;import java.util.Scanner;public class March0317 {public …
阅读更多...
【鸿蒙HarmonyOS开发笔记】常用组件介绍篇 —— Toggle切换按钮组件

【鸿蒙HarmonyOS开发笔记】常用组件介绍篇 —— Toggle切换按钮组件

概述 Toggle为切换按钮组件&#xff0c;一般用于两种状态之间的切换&#xff0c;例如下图中的蓝牙开关。 参数 Toggle组件的参数定义如下 Toggle(options: { type: ToggleType, isOn?: boolean })● type type属性用于设置Toggle组件的类型&#xff0c;可通过ToggleType枚举…
阅读更多...
无人机助力智慧农田除草新模式，基于YOLOv7【tiny/l/x】不同系列参数模型开发构建无人机航拍场景下的农田杂草检测识别系统

无人机助力智慧农田除草新模式，基于YOLOv7【tiny/l/x】不同系列参数模型开发构建无人机航拍场景下的农田杂草检测识别系统

科技发展到今天&#xff0c;无人机喷洒药物已经不是一件新鲜事情了&#xff0c;在很多高危的工作领域中&#xff0c;比如高空电力设备除冰&#xff0c;电力设备部件传送更换等等&#xff0c;无人机都可以扮演非常出色的作用&#xff0c;前面回到老家一段时间&#xff0c;最近正…
阅读更多...
Leetcode 31. 删除无效的括号

Leetcode 31. 删除无效的括号

心路历程&#xff1a; 一开始看到有点懵&#xff0c;后来发现有点像按照一定规则穷举所有可能情况&#xff0c;想到了排列组合问题&#xff0c;再结合问题长度不固定&#xff0c;无法用已知个for循环表示&#xff0c;从而想到了回溯。这个题相当于需要在一定规则下枚举。 按照…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023