概述
- 本篇为
ShapePoints静态函数库的补充和辅助文档。 ShapePoints函数库是一个用于生成常见几何图形顶点数据(PackedVector2Array)的静态函数库。- 生成的数据可用于
_draw和Line2D、Polygon2D等进行绘制和显示。 - 因为不断地持续扩展,
ShapePoints函数库的函数数目在不断增加,同时涉及的图形类型也在发生变化。 - 本篇按照一定的分类,阐述每个图形函数的原理和具体实现,以及具体使用。
注意:本篇基础内容写于2023年7月,由3篇文章汇总而成。ShapePoints函数库及其使用会单独发文贴出。本篇更接近原理讲解。
基础原理
- 在一个平面中,确定一个直角坐标系后,平面上任意一点位置就可以用
(x,y)这样的值对来表示,(x,y)可以被称为这个点的坐标。 - 同样这个点
(x,y)也可以理解为相对于坐标系原点(0,0),水平移动了x,垂直移动了y,也就是一个由原点指向(x,y)的向量。 - 通过平面向量的加减乘除以及旋转操作,我们获得新的点的位置,一系列点的位置可以被顺序用线段连接起来,构成PolyLine(折线)或PolyGon(多边形,闭合的折线)
- 这些点数据可以用于
_draw和Line2D、Polygon2D等绘制和显示几何图形
基础图形
矩形
矩形最简单,计算出4个顶点就行。其运算不过是一些简单的向量加减法。

实现代码
# 返回矩形的顶点
static func rect(size:Vector2,offset:Vector2 = Vector2.ZERO) -> PackedVector2Array:
var points:PackedVector2Array = [
offset,
offset + Vector2.RIGHT * size.x,
offset + size,
offset + Vector2.DOWN * size.y,
offset]
return points
正多边形
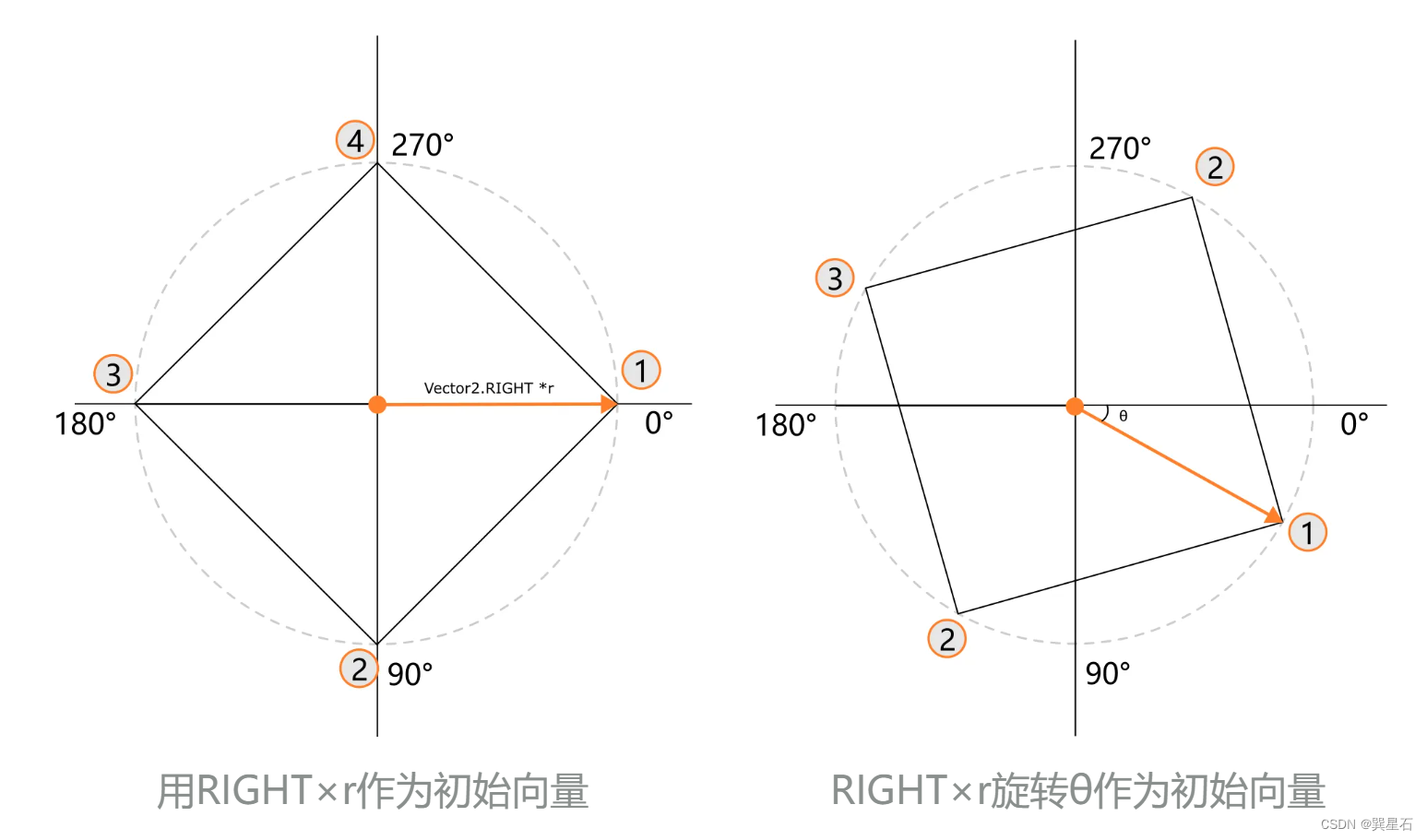
求正多边形的顶点,其本质是求圆上等分的点。可以通过向量旋转法求取。起始角度不同,图形发生相应旋转。
实现代码
# 返回正多边形顶点
static func regular_polygon(start_angle:int,edges:int,r:float,offset:Vector2 = Vector2.ZERO):
var points:PackedVector2Array
var vec = Vector2.RIGHT.rotated(deg_to_rad(start_angle)) * r
for i in range(edges):
points.append(vec.rotated(2* PI/edges * i) + offset)
return points
圆
圆是边数很多的正多边形。问题在于这个边数计算,怎样才能保证任何半径下圆都看起来很平滑。
我的方法简单粗暴,边数直接等于2πr,也就是周长。这等于无论圆的半径是多少,它都要包含2πr个顶点。
实现代码
# 返回圆顶点
static func circle(r:float,offset:Vector2 = Vector2.ZERO):
var points = regular_polygon(0,2 * PI * r,r,offset)
points.append(points[0])
return points
扇形
扇形是圆的一部分,起始和终止点都是圆心,从而组成闭合图形。
圆弧部分可以通过向量旋转求取的,具体调用弧形函数arc就可以。

实现代码
# 返回扇形顶点
# 注意start_angle和end_angle都是角度
static func sector(start_angle:int,end_angle:int,r:float):
var points:PackedVector2Array
points.append(Vector2.ZERO)
points.append_array(arc(start_angle,end_angle,r))
points.append(Vector2.ZERO)
return points
弧形
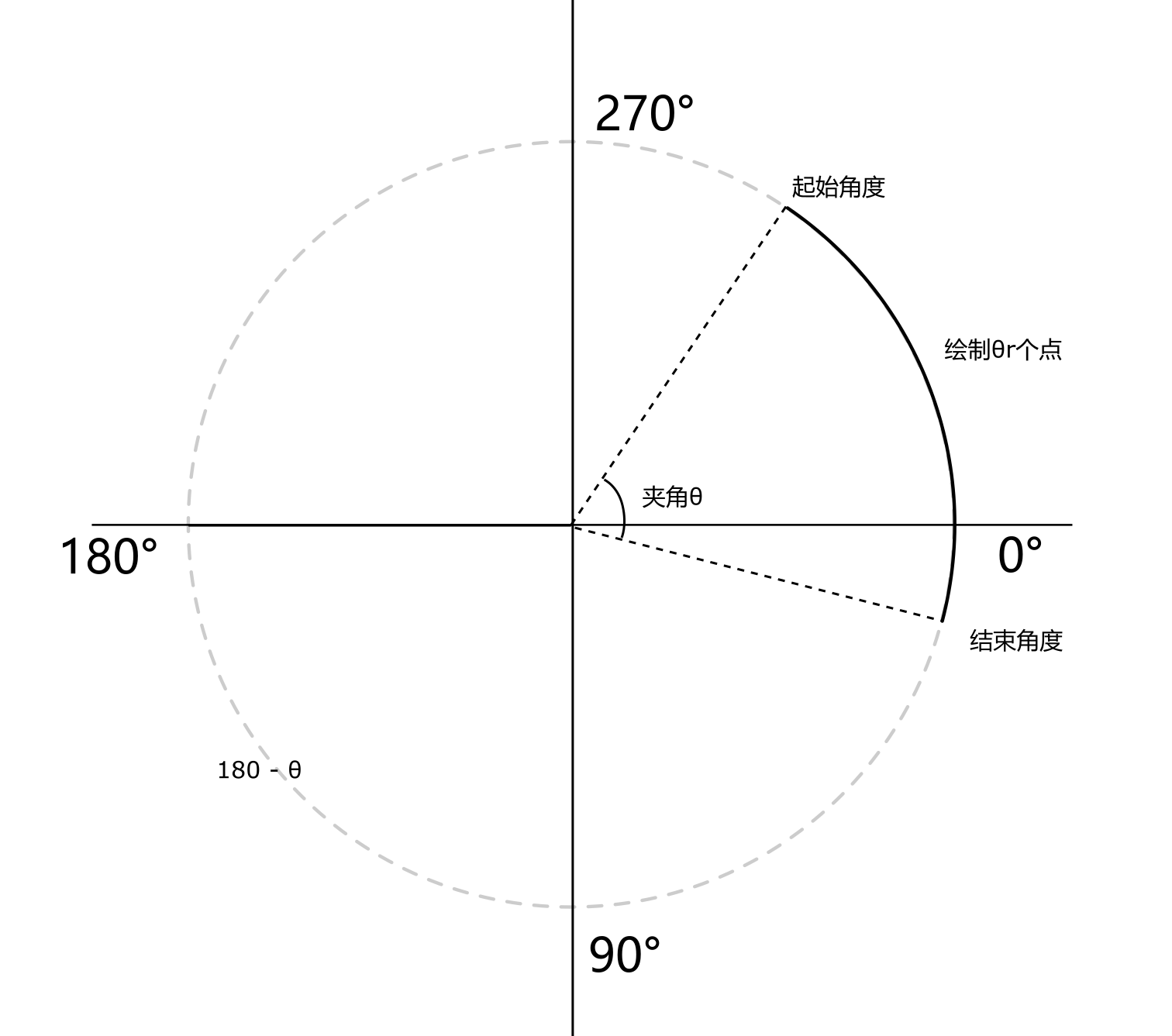
弧形是扇形去掉起始点也就是圆心之后的图形。
同样为了始终保持平滑效果,绘制的点个数是与r的大小相关的,即始终绘制θ×r个点。
θ为起始角度和结束角度之间的夹角的弧度值。
实现代码
# 弧形
# 注意start_angle和end_angle都是角度
static func arc(start_angle:int,end_angle:int,r:float,offset:Vector2 = Vector2.ZERO):
var points:PackedVector2Array
var angle = deg_to_rad(end_angle - start_angle)
var edges:float = ceilf(angle * r) # 要绘制的点的个数 = θ * r
var vec = Vector2.RIGHT.rotated(deg_to_rad(start_angle)) * r
for i in range(edges+1):
points.append(vec.rotated(angle/edges * i) + offset)
return points
星形
星形是在两个半径不同的同心圆上求正多边形顶点。也是采用向量旋转法。

实现代码
# 星形
static func star(start_angle:int,edges:int,r:float,r2:float = 0,offset:Vector2 = Vector2.ZERO):
if r2 == 0:
r2 = r/2.0
var points:PackedVector2Array
# 外部半径
var vec = Vector2.RIGHT.rotated(deg_to_rad(start_angle)) * r
# 内部半径
var vec2 = Vector2.RIGHT.rotated(deg_to_rad(start_angle + 180/edges)) * r2
for i in range(edges):
points.append(vec.rotated(2 * PI/edges * i) + offset)
points.append(vec2.rotated(2 * PI/edges * i) + offset)
return points
圆角矩形
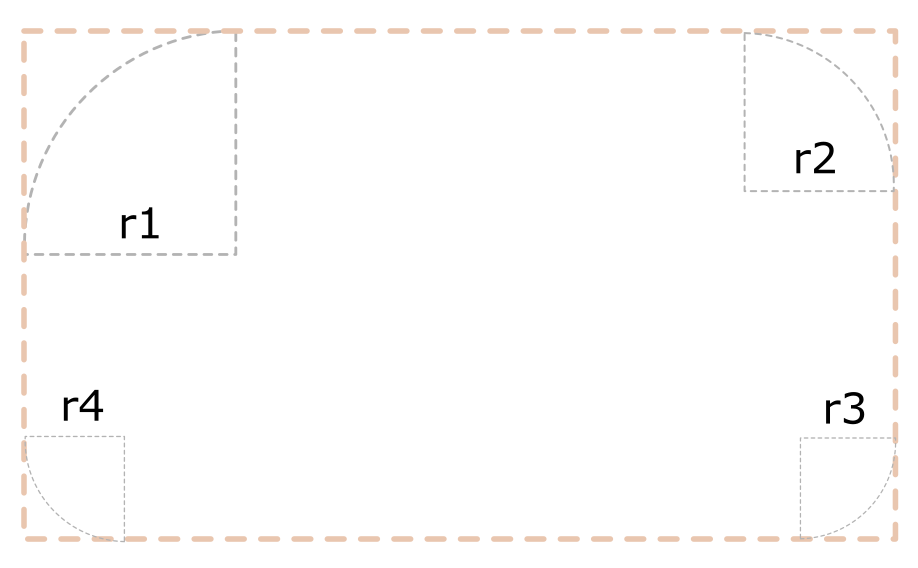
本质是在矩形四个角上绘制1/4圆弧。
实现代码
# 返回圆角矩形的顶点
# 注意:以(0,0)为几何中心
static func round_rect(size:Vector2,r1:float,r2:float,r3:float,r4:float,offset:Vector2 = Vector2.ZERO) -> PackedVector2Array:
var points:PackedVector2Array
points.append_array(arc(180,270,r1,Vector2(r1,r1) + offset))
points.append_array(arc(270,360,r2,Vector2(size.x - r2,r2) + offset))
points.append_array(arc(0,90,r3,Vector2(size.x - r3,size.y -r3) + offset))
points.append_array(arc(90,180,r4,Vector2(r4,size.y - r4) + offset))
points.append(Vector2(0,r1)+offset)
return points
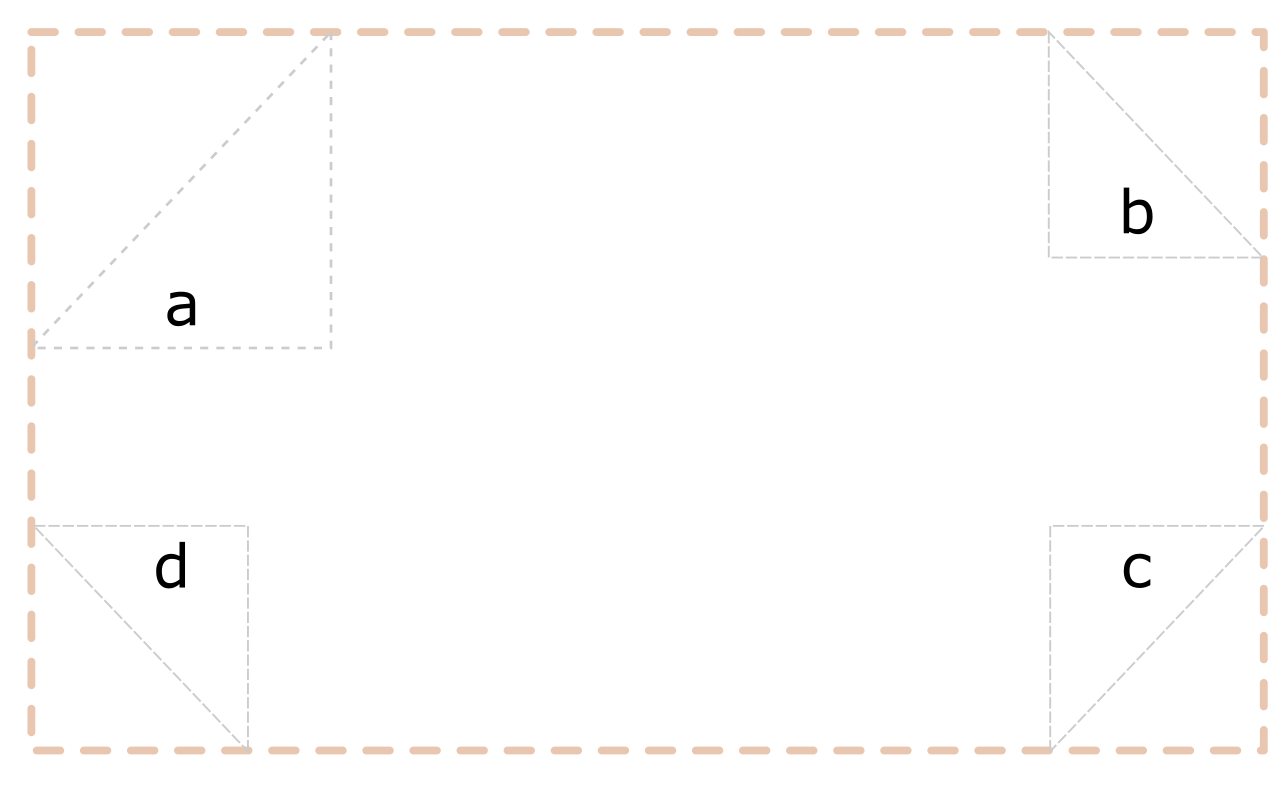
倒角矩形
倒角矩形跟圆角矩形很像,只是更简单了,不用在四个角上画圆弧了,而是从矩形的4个顶点变为计算8个顶点。
实现代码
# 返回倒角矩形的顶点
# 注意:以(0,0)为几何中心
static func chamfer_rect(size:Vector2,a:float,b:float,c:float,d:float,offset:Vector2 = Vector2.ZERO) -> PackedVector2Array:
var points:PackedVector2Array = [
Vector2(0,a) + offset,Vector2(a,0) + offset,
Vector2(size.x-b,0) + offset,Vector2(size.x,b) + offset,
Vector2(size.x,size.y-c) + offset,Vector2(size.x-c,size.y) + offset,
Vector2(d,size.y) + offset,Vector2(0,size.y-d) + offset
]
points.append(points[0]) # 闭合
return points
胶囊形
胶囊形的本质是两个水平或垂直方向上的半圆弧+一定的偏移距离。

实现代码
# 返回胶囊形的顶点
static func capsule(size:Vector2,offset:Vector2 = Vector2.ZERO) -> PackedVector2Array:
var points:PackedVector2Array = []
var r:float = min(size.x,size.y)/2.0
if size.x>size.y: # 横向
points.append_array(arc(90,270,r,Vector2(r,r) + offset))
points.append_array(arc(-90,90,r,Vector2(size.x-r,r) + offset))
else: # 纵向
points.append_array(arc(180,360,r,Vector2(r,r) + offset))
points.append_array(arc(0,180,r,Vector2(r,size.y-r) + offset))
points.append(points[0]) # 闭合
return points
@tool
extends Control
func _draw():
var size = get_rect().size
draw_polyline(ShapePoints.capsule(size),Color.GREEN_YELLOW,1)
效果:

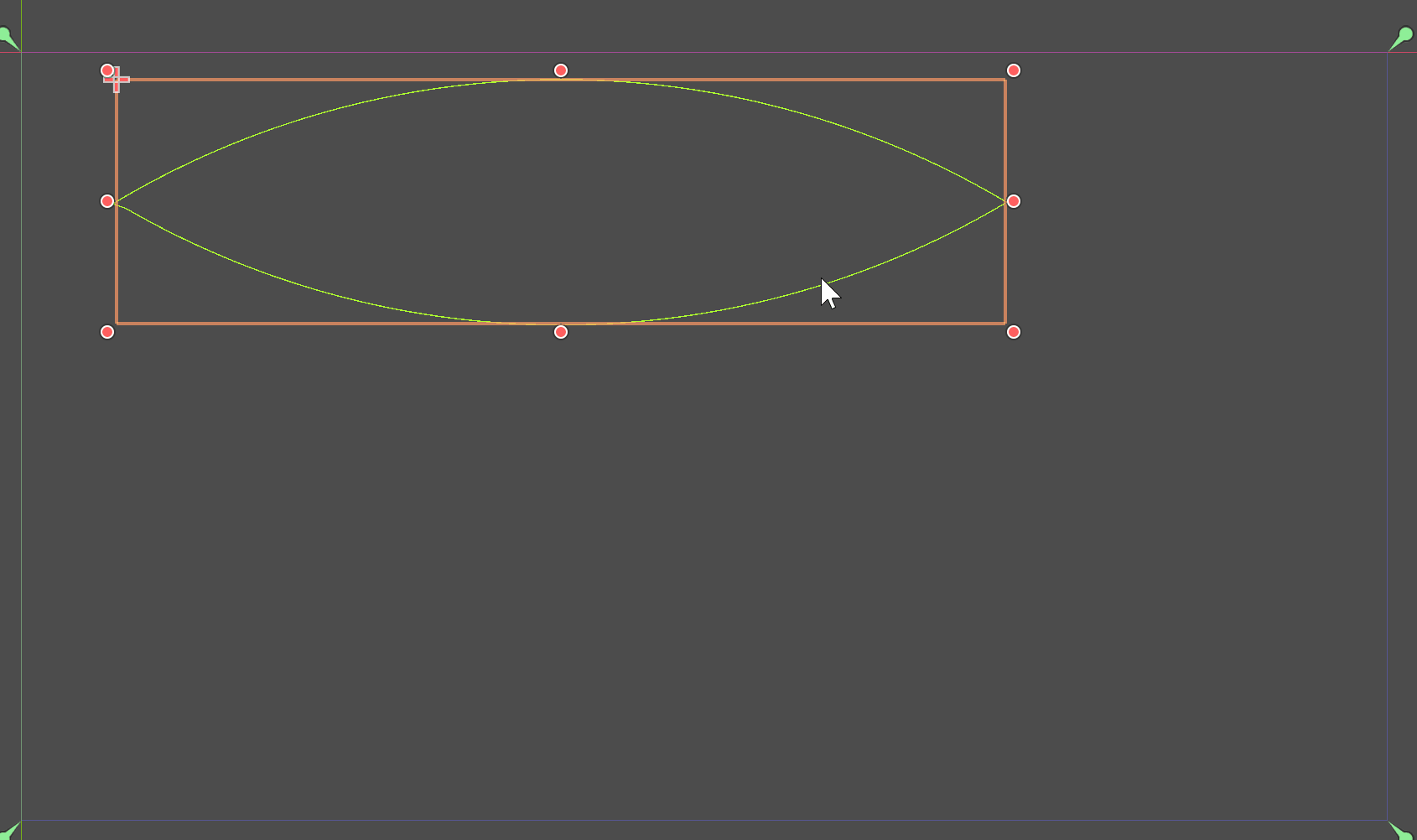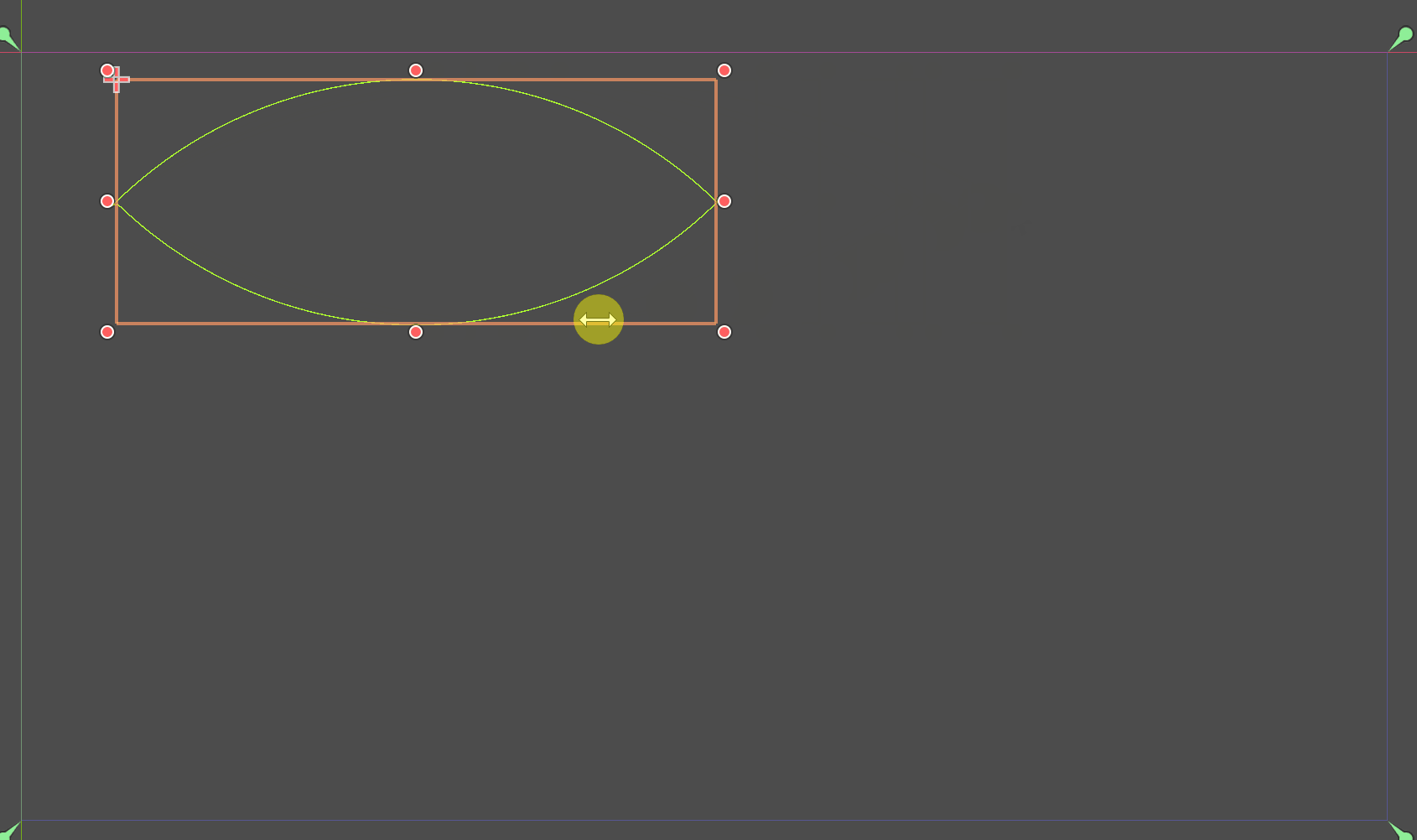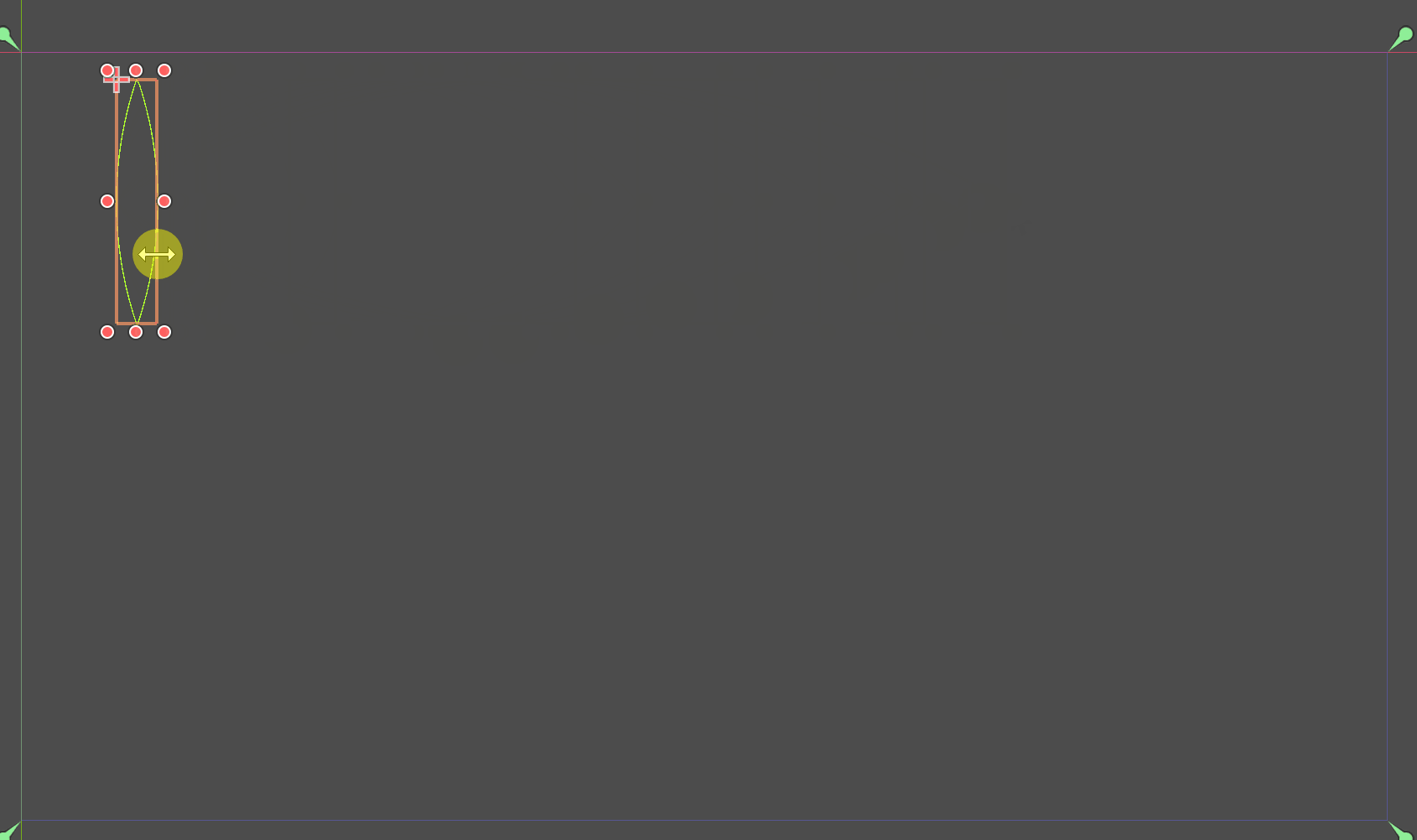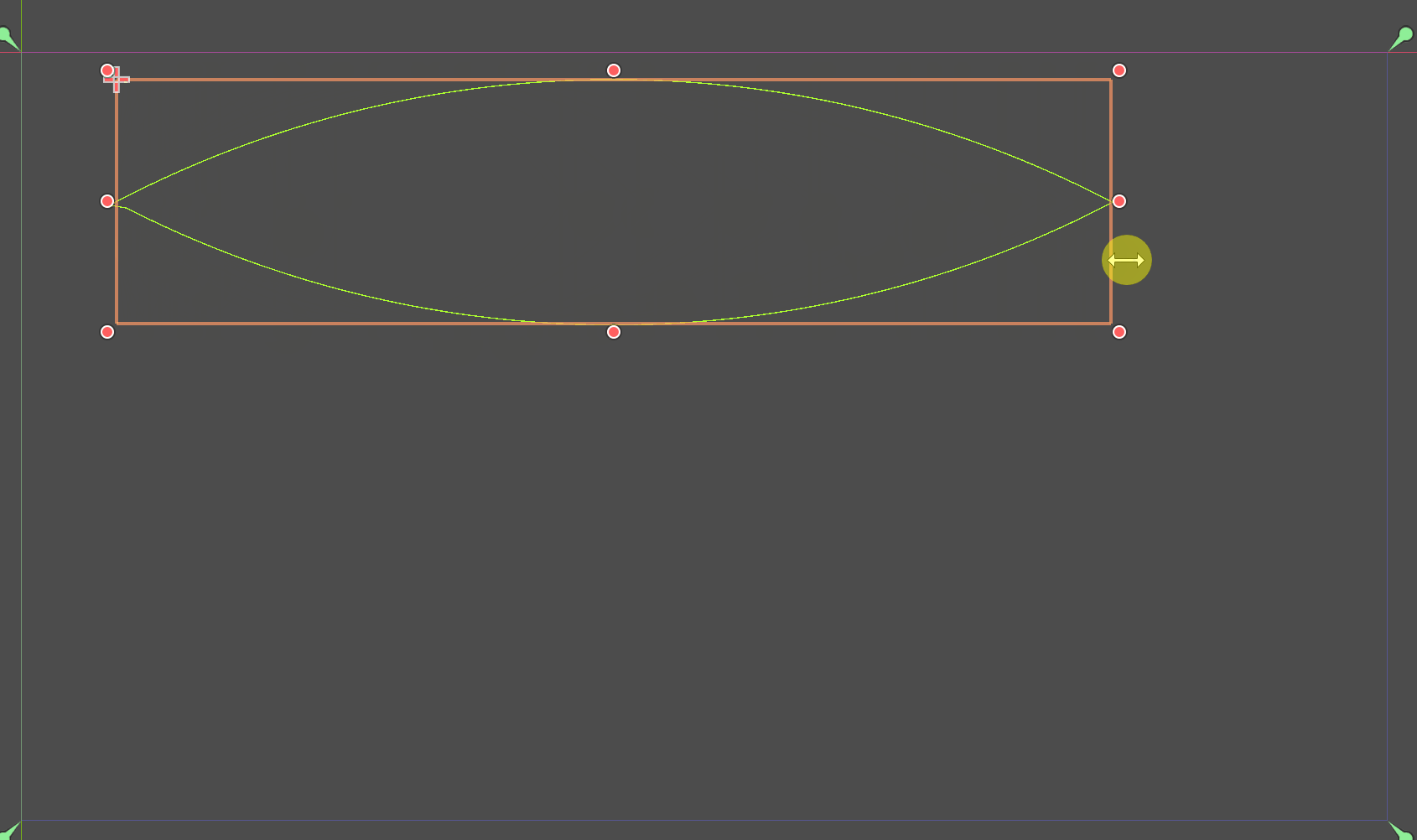
梭形
梭形的本质是绘制两段在X轴或Y轴上对称的圆弧。而圆弧需要的就是半径、起始角度和结束角度。
所以问题就变成了求半径和角度的问题。

可以知道:
r
2
=
d
y
2
+
(
r
−
d
x
)
2
r^2 = dy^2+(r-dx)^2
r2=dy2+(r−dx)2
也就是: r 2 = d y 2 + r 2 − 2 r d x + d x 2 r^2 = dy^2+r^2-2rdx + dx^2 r2=dy2+r2−2rdx+dx2
两侧消去 r 2 r^2 r2,就变成 2 r d x = d y 2 + d x 2 2rdx = dy^2+dx^2 2rdx=dy2+dx2
最终半径 r = ( d y 2 + d x 2 ) / 2 d x r = (dy^2+dx^2)/2dx r=(dy2+dx2)/2dx
而因为 s i n θ = d y / r sinθ = dy/r sinθ=dy/r,所以 θ = a r c s i n ( d y / r ) θ = arcsin(dy/r) θ=arcsin(dy/r)。
有了半径r和二分之一的夹角θ,就可以求圆弧了,反向的圆弧也可以求出。
实现代码
# 返回梭形的顶点
# 注意:以(0,0)为几何中心
static func spindle(size:Vector2,offset:Vector2 = Vector2.ZERO) -> PackedVector2Array:
var points:PackedVector2Array = []
var dx:float = size.x/2.0
var dy:float = size.y/2.0
var d_max = max(dx,dy)
var d_min = min(dx,dy)
var r = (pow(d_max,2.0) + pow(d_min,2.0))/(2.0 * d_min) # 圆弧半径
var angle = rad_to_deg(asin(d_max/r))
if dx<dy:
points.append_array(arc(180-angle,180+angle,r,Vector2(r,dy)))
points.append(Vector2(dx,0))
points.append_array(arc(-angle,angle,r,Vector2(-r+2*dx+1,dy)))
points.append(points[0]) # 闭合
else:
points.append_array(arc(270-angle,270+angle,r,Vector2(dx,r)))
points.append(Vector2(size.x,dy))
points.append_array(arc(90-angle,90+angle,r,Vector2(dx,-r+2*dy+1)))
points.append(points[0]) # 闭合
return points
效果测试
@tool
extends Control
func _draw():
var size = get_rect().size
draw_polyline(ShapePoints.spindle(size),Color.GREEN_YELLOW,1)
效果:
特殊图形
太极图
最主要的阴阳鱼,几何组成却十分简单:可以看成是一个大半圆弧和两个反向的小半圆弧连接形成的。

函数
# 太极
static func taiji(r:float,offset:Vector2 = Vector2.ZERO) -> Dictionary:
var dict = {
pan = circle(r,offset), # 底部圆盘
yin = [], # 阴鱼
yang = [], # 阳鱼
yin_eye = circle(r/10,Vector2(0,-r/2)+ offset), # 阴鱼眼
yang_eye = circle(r/10,Vector2(0,r/2)+ offset), # 阳鱼眼
}
# 阴鱼
dict["yin"].append_array(arc(90,270,r,offset))
dict["yin"].append_array(arc(-90,90,r/2,Vector2(0,-r/2)+offset))
var ac = arc(90,270,r/2,Vector2(0,r/2)+offset)
ac.reverse()
dict["yin"].append_array(ac)
# 阳鱼
dict["yang"].append_array(arc(-90,90,r,offset))
dict["yang"].append_array(arc(90,270,r/2,Vector2(0,r/2)+offset))
var ac2 = arc(-90,90,r/2,Vector2(0,-r/2)+offset)
ac2.reverse()
dict["yang"].append_array(ac2)
return dict
绘制测试
@tool
extends Control
func _draw():
var rect = get_rect()
var center = rect.get_center()
var r = rect.size.y/2
var w = rect.size.x - 10
var offset = center
var taiji = ShapePoints.taiji(r,offset)
for point in taiji["yin"]:
draw_circle(point,0.5,Color.CHARTREUSE)
draw_polyline(taiji["yin"],Color.AQUA,1)
draw_polyline(taiji["yang"],Color.AQUA,1)
draw_polyline(taiji["yin_eye"],Color.AQUA,1)
draw_polyline(taiji["yang_eye"],Color.AQUA,1)
效果:

螺旋线
暂时还不是很完美。
函数
# 螺旋线
static func helix(start_angle:int,start_r:float,end_r:float,
step:int =1,offset:Vector2 = Vector2.ZERO) -> PackedVector2Array:
var points:PackedVector2Array
var steps = end_r - start_r
for i in range(steps):
points.append(Vector2.RIGHT.rotated(deg_to_rad(start_angle + step * i)) * (start_r+i) + offset)
return points
测试
@tool
extends Control
func _draw():
var rect = get_rect()
var center = rect.get_center()
draw_polyline(ShapePoints.helix(0,0,rect.size.y * 2,1,center),Color.GREEN_YELLOW,2)
效果:

各种网格
矩形网格
最好是能够将网格绘制也像刻度线求取函数一样,封装成函数,通过传入参数后返回横线竖线线的集合,然后具体绘制可以在任何节点中进行。
函数化的好处还在于,你可以求取不同参数下的网格线,然后具体绘制的时候使用不同的粗细、颜色等。搭配起来可以绘制更复杂的网格线,比如心电图纸的大小格设计。
# 方形 - 网格线求取函数
static func rect_grid_lines(size:Vector2,cell_size:Vector2) -> Dictionary:
var lines = {
v_lines = [], # 垂直的网格线
h_lines = [] # 水平的网格线
}
var v_line1 = [Vector2.ZERO,Vector2.DOWN * cell_size.y * size.y]
var h_line1 = [Vector2.ZERO,Vector2.RIGHT * cell_size.x * size.x]
lines["v_lines"].append(v_line1)
lines["h_lines"].append(h_line1)
for x in range(1,size.x+1):
var offset_x = Vector2(cell_size.x,0) * x
lines["v_lines"].append([v_line1[0] + offset_x,v_line1[1] + offset_x])
for y in range(1,size.y+1):
var offset_y = Vector2(0,cell_size.y) * y
lines["h_lines"].append([h_line1[0] + offset_y,h_line1[1] + offset_y])
return lines
@tool
extends Control
func _draw():
var grid = ShapePoints.rect_grid_lines(Vector2(10,10),Vector2(50,50))
# 绘制垂直线
for line in grid["v_lines"]:
draw_line(line[0],line[1],Color.GREEN_YELLOW,2)
# 绘制水平线
for line in grid["h_lines"]:
draw_line(line[0],line[1],Color.GREEN_YELLOW,2)

绘制函数
因为_draw和draw_*之类的只能在CanvasItem类型及其子节点中使用,并且不能用于编写静态函数,所以好的办法就剩下将点、线之类的求取做成函数,而在实际的扩展节点中在基于这些求取函数编写进一步的绘制函数。
@tool
extends Control
func _draw():
draw_grid(Vector2(10,10),Vector2(50,50))
# 绘制网格函数
func draw_grid(size:Vector2,cell_size:Vector2,border_color:Color = Color.GREEN_YELLOW,border_width = 1) -> void:
var grid = ShapePoints.rect_grid_lines(size,cell_size)
# 绘制垂直线
for line in grid["v_lines"]:
draw_line(line[0],line[1],border_color,border_width)
# 绘制水平线
for line in grid["h_lines"]:
draw_line(line[0],line[1],border_color,border_width)
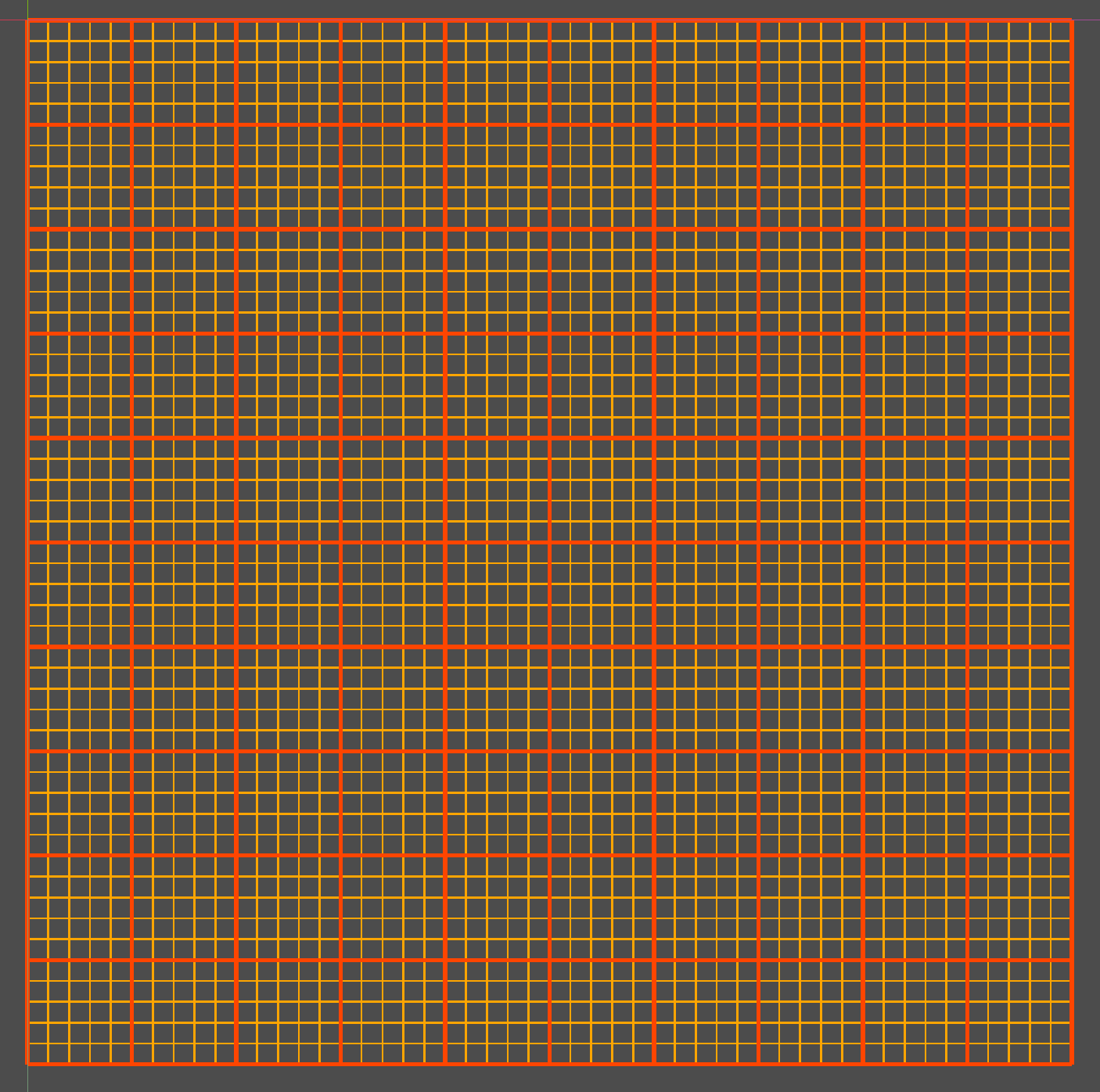
网格线求取和网格线绘制函数的好处是,你可以轻松的基于其创建复杂的网格,比如下面这样的:
@tool
extends Control
func _draw():
draw_grid(Vector2(50,50),Vector2(10,10),Color.ORANGE)
draw_grid(Vector2(10,10),Vector2(50,50),Color.ORANGE_RED,2)
矩形点网格
再绘制原点网格或十字网格的时候,要的不再是一条条的线,而是网格的交点。
# 方形 - 网格点求取函数
static func rect_grid_points(size:Vector2,cell_size:Vector2) ->PackedVector2Array:
var points:PackedVector2Array
for x in range(size.x + 1):
for y in range(size.y + 1):
points.append(Vector2(x,y) * cell_size)
return points
绘制函数
同样的我们可以在自定义控件内部定义参数化的点网格绘制函数:
# 绘制点网格函数
func draw_point_grid(size:Vector2,cell_size:Vector2,point_color:Color = Color.GREEN_YELLOW,r = 2) -> void:
for point in ShapePoints.rect_grid_points(size,cell_size):
draw_circle(point,r,point_color)
使用:
@tool
extends Control
func _draw():
draw_point_grid(Vector2(10,10),Vector2(50,50),Color.GREEN_YELLOW,5)

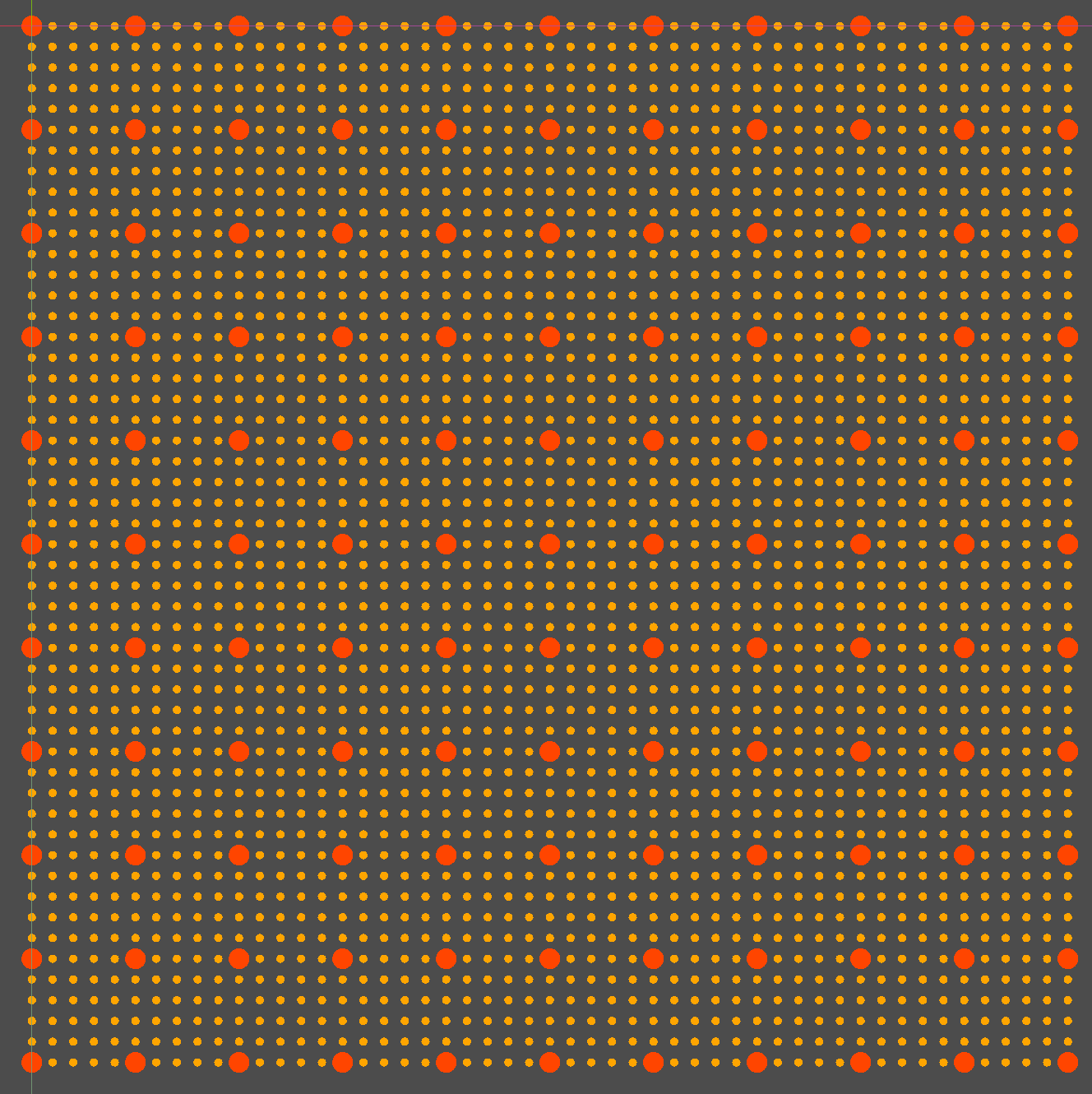
也可以使用不同参数的多个点网格叠加:
@tool
extends Control
func _draw():
draw_point_grid(Vector2(50,50),Vector2(10,10),Color.ORANGE)
draw_point_grid(Vector2(10,10),Vector2(50,50),Color.ORANGE_RED,5)
十字线网格
# 返回指定点为中心,给定长度的两条互相垂直线段,可以用于绘制十字坐标线
static func line_cross(position:Vector2,length:float,start_angle:int = 0) -> Array:
# 水平线段俩端点
var h_line = [
Vector2.LEFT.rotated(start_angle) * length/2.0 + position,
Vector2.RIGHT.rotated(start_angle) * length/2.0 + position,
]
# 水平线段俩端点
var v_line = [
Vector2.UP.rotated(start_angle) * length/2.0 + position,
Vector2.DOWN.rotated(start_angle) * length/2.0 + position,
]
return [h_line,v_line]
绘制函数
控件内部绘制十字线网格函数:
# 绘制十字网格函数
func draw_line_cross_grid(size:Vector2,cell_size:Vector2,color:Color = Color.GREEN_YELLOW,length = 10,start_angle:int = 0):
for point in ShapePoints.rect_grid_points(size,cell_size):
var line_cross = ShapePoints.line_cross(point,length,start_angle)
draw_line(line_cross[0][0],line_cross[0][1],Color.GREEN_YELLOW,1)
draw_line(line_cross[1][0],line_cross[1][1],Color.GREEN_YELLOW,1)
使用:
@tool
extends Control
func _draw():
draw_line_cross_grid(Vector2(10,10),Vector2(50,50))

旋转45度
因为设定了start_angle参数,所以理论上你可以任意设定十字的旋转角度,甚至将其做成动画。
@tool
extends Control
func _draw():
draw_line_cross_grid(Vector2(10,10),Vector2(50,50),Color.GREEN_YELLOW,10,45)

三角点网格

特点是:
- 偶数行不偏移,绘制
n+1个点 - 奇数行向右半偏移,并且点数比奇数行少
1
# 三角 - 网格点求取函数
static func triangle_grid_points(size:Vector2,cell_size:Vector2) ->PackedVector2Array:
var points:PackedVector2Array
for y in range(size.y + 1):
if y % 2 == 0: # 偶数行
for x in range(size.x + 1):
points.append(Vector2(x,y) * cell_size)
else: # 奇数行
for x in range(size.x):
points.append(Vector2(x,y) * cell_size + Vector2(cell_size.x/2,0))
return points
绘制函数
# 绘制三角网格 - 点网格函数
func draw_triangle_point_grid(size:Vector2,cell_size:Vector2,point_color:Color = Color.GREEN_YELLOW,r = 2) -> void:
for point in ShapePoints.triangle_grid_points(size,cell_size):
draw_circle(point,r,point_color)

六边形点网格

六边形网格的顶点可以在三角网格点的基础上轻松获取,规律就是:
- 将奇偶行调换一下位置,也就是偶数行进行半偏移,而奇数行不进行偏移
- 偶数行:
(x+1) % 3 == 0时不画点 - 奇数行:
x % 3 == 1时不画点
# 六边形 - 网格点求取函数
static func hex_grid_points(size:Vector2,cell_size:Vector2) ->PackedVector2Array:
var points:PackedVector2Array
for y in range(size.y + 1):
if y % 2 == 0: # 偶数行
for x in range(size.x):
if (x+1)% 3 != 0:
points.append(Vector2(x,y) * cell_size + Vector2(cell_size.x/2,0))
else: # 奇数行
for x in range(size.x + 1):
if x % 3 != 1:
points.append(Vector2(x,y) * cell_size)
return points
绘制函数
# 绘制六边形网格 - 点网格函数
func draw_hex_point_grid(size:Vector2,cell_size:Vector2,point_color:Color = Color.GREEN_YELLOW,r = 2) -> void:
for point in ShapePoints.hex_grid_points(size,cell_size):
draw_circle(point,r,point_color)
使用:
@tool
extends Control
func _draw():
draw_hex_point_grid(Vector2(10,10),Vector2(50,50),Color.GREEN_YELLOW,5)

@tool
extends Control
func _draw():
draw_hex_point_grid(Vector2(30,30),Vector2(20,20),Color.ORANGE,2)

棋盘格
# 矩形网格 - 棋盘格矩形求取函数
static func checker_board_rects(size:Vector2,cell_size:Vector2) -> Array:
var rects_yang:Array[Rect2]
var rects_yin:Array[Rect2]
for x in range(size.x):
for y in range(size.y):
var pos = Vector2(x,y) * cell_size
if (x % 2 == 0 and y % 2 == 0) or (x % 2 == 1 and y % 2 == 1):
rects_yang.append(Rect2(pos,cell_size))
else:
rects_yin.append(Rect2(pos,cell_size))
return [rects_yang,rects_yin]
绘制函数
# 矩形棋盘格绘制函数
func draw_checker_board_grid(
size:Vector2,
cell_size:Vector2,
yang_color:Color = Color.WHITE,
yin_color:Color = Color.DIM_GRAY,
draw_grid_lines:bool = false,
border_color:Color = Color.DIM_GRAY.darkened(0.5),
border_width:int = 1
) -> void:
var grid = ShapePoints.checker_board_rects(size,cell_size)
var rects_yang:Array[Rect2] = grid[0]
var rects_yin:Array[Rect2] = grid[1]
for rect in rects_yang:
draw_rect(rect,yang_color)
for rect in rects_yin:
draw_rect(rect,yin_color)
if draw_grid_lines: # 绘制网格线
draw_line_grid(size,cell_size,border_color,border_width)
使用:
@tool
extends Control
func _draw():
draw_checker_board_grid(Vector2(9,9),Vector2(20,20))

@tool
extends Control
func _draw():
draw_checker_board_grid(Vector2(9,9),Vector2(20,20),Color.ORANGE_RED,Color.ORANGE,true)

@tool
extends Control
func _draw():
draw_checker_board_grid(Vector2(9,9),Vector2(20,20),Color.GREEN_YELLOW,Color.YELLOW,true,Color.GREEN_YELLOW.darkened(0.2),1)

刻度线
弧形刻度线
概述
在制作一些钟表、压力表以及其他一些控件时,存在弧形刻度或圆形刻度线绘制需求,为了减少重复造轮子,搞了一个函数。
它可以轻松的求取和返回指定参数的弧形刻度线集合。
# 返回指定范围的弧形刻度线起始点坐标集合
# start_angle:起始角度
# end_angle:结束角度
# steps:切分次数
# r:半径
# length:刻度线长
func arc_scale(start_angle:int,end_angle:int,steps:int,r:float,length:float) -> Array:
var scales:Array = []
var vec1 = (Vector2.RIGHT * (r-length)).rotated(deg_to_rad(start_angle))
var vec2 = (Vector2.RIGHT * r).rotated(deg_to_rad(start_angle))
var angle = deg_to_rad(end_angle - start_angle) # 夹角
for i in range(steps+1):
var line = [vec1.rotated((angle/steps) * i),vec2.rotated((angle/steps) * i)]
scales.append(line)
return scales
通过遍历返回的刻度线起始坐标,就可以绘制刻度线了。
绘制钟表刻度
@tool
extends Control
func _draw():
var rect = get_rect()
var center = rect.get_center()
var r = rect.size.y/2
draw_circle(center,r,Color.AZURE)
# 绘制基础刻度
var lines = arc_scale(-90,270,12,r,10)
for line in lines:
draw_line(line[0]+center,line[1]+center,Color.AQUA,2)
var lines2 = arc_scale(-90,270,60,r,5)
for line in lines2:
draw_line(line[0]+center,line[1]+center,Color.AQUA,1)

绘制压力表刻度
@tool
extends Control
func _draw():
var rect = get_rect()
var center = rect.get_center()
var r = rect.size.y/2
draw_circle(center,r,Color.AZURE)
# 最细刻度
var lines3 = arc_scale(-(270-45),90-45,60,r,4)
for line in lines3:
draw_line(line[0]+center,line[1]+center,Color.AQUA,1)
# 中刻度
var lines2 = arc_scale(-(270-45),90-45,12,r,8)
for line in lines2:
draw_line(line[0]+center,line[1]+center,Color.AQUA,1)
# 大刻度
var lines = arc_scale(-(270-45),90-45,6,r,10)
for line in lines:
draw_line(line[0]+center,line[1]+center,Color.CADET_BLUE,2)

直线刻度
函数
# 返回指定范围的直线刻度线起始点坐标集合
func line_scale(ruler_width:float,steps:int,length:float):
var scales:Array = []
var vec1 = Vector2.ZERO
var vec2 = Vector2.DOWN * length
var space = ruler_width/steps # 单位间隔
for i in range(steps+1):
var line = [vec1 + Vector2(space,0) * i,vec2 + Vector2(space,0) * i]
scales.append(line)
return scales
绘制直尺刻度
@tool
extends Control
func _draw():
var rect = get_rect()
var center = rect.get_center()
var r = rect.size.y/2
var w = rect.size.x - 10
var offset = Vector2(5,5)
draw_rect(rect,Color("orange").lightened(0.2))
draw_rect(Rect2(Vector2.ZERO,Vector2(rect.size.x,20)),Color("orange").lightened(0.4))
# 最细刻度
var lines = line_scale(w,100,5)
for line in lines:
draw_line(line[0]+offset,line[1]+offset,Color("#444").lightened(0.5),1)
# 最细刻度
var lines2 = line_scale(w,20,8)
for line in lines2:
draw_line(line[0]+offset,line[1]+offset,Color("#444").lightened(0.4),1)
# 最细刻度
var lines3 = line_scale(w,10,10)
for line in lines3:
draw_line(line[0]+offset,line[1]+offset,Color("#444").darkened(0.4),2)