DP最长上升子序列模型

怪盗基德的滑翔翼
- 代码实现
登山
- 代码实现
合唱队形
- 代码实现
友好城市
- 问题分析
- 代码实现
最大上升子序列和
- 代码实现
*拦截导弹
- 问题分析
- 代码实现
- 扩展
*导弹防御系统
- 问题分析
- 代码实现
*最长公共上升子序列
- 问题分析
- 代码实现

LIS 问题一般有三种解法

朴素版动态规划
贪心+二分
树状数组

怪盗基德的滑翔翼

题目描述：

怪盗基德是一个充满传奇色彩的怪盗，专门以珠宝为目标的超级盗窃犯。

而他最为突出的地方，就是他每次都能逃脱中村警部的重重围堵，而这也很大程度上是多亏了他随身携带的便于操作的滑翔翼。

有一天，怪盗基德像往常一样偷走了一颗珍贵的钻石，不料却被柯南小朋友识破了伪装，而他的滑翔翼的动力装置也被柯南踢出的足球破坏了。

不得已，怪盗基德只能操作受损的滑翔翼逃脱。

假设城市中一共有 $N$ 幢建筑排成一条线，每幢建筑的高度各不相同。

初始时，怪盗基德可以在任何一幢建筑的顶端。

他可以选择一个方向逃跑，但是不能中途改变方向（因为中森警部会在后面追击）。

因为滑翔翼动力装置受损，他只能往下滑行（即：只能从较高的建筑滑翔到较低的建筑）。

他希望尽可能多经过不同建筑的顶部，这样可以减缓下降时的冲击力，减少受伤的可能性。

请问，他最多可以经过多少幢不同建筑的顶部(包含初始时的建筑)？

输入格式：

输入数据第一行是一个整数 $K$ ，代表有 $K$ 组测试数据。

每组测试数据包含两行：第一行是一个整数 $N$ ，代表有 $N$ 幢建筑。第二行包含 $N$ 个不同的整数，每一个对应一幢建筑的高度h，按照建筑的排列顺序给出。

输出格式：

对于每一组测试数据，输出一行，包含一个整数，代表怪盗基德最多可以经过的建筑数量。

数据范围：

$1 \leq K \leq 100$
$1 \leq N \leq 100$
$0 < h < 10000$

输入样例：

3
8
300 207 155 299 298 170 158 65
8
65 158 170 298 299 155 207 300
10
2 1 3 4 5 6 7 8 9 10

输出样例：

6
6
9

代码实现

拆解为从左往右和从右往左的两个最长上升子序列来进行求解

import sys
input = sys.stdin.readline

k = int(input().strip())
for _ in range(k):
    n = int(input().strip())
    nums = list(map(int, input().strip().split()))
    ans1 = ans2 = 0
    f = [1] * n
    for i in range(n):
        f[i] += max((f[j] for j in range(i) if nums[j] > nums[i]), default=0)
        ans1 = max(ans1, f[i])
    f = [1] * n
    for i in range(n - 1, -1, -1):
        f[i] += max((f[j] for j in range(i + 1, n) if nums[j] > nums[i]), default=0)
        ans2 = max(ans2, f[i])
    print(max(ans1, ans2))

登山

题目描述：
五一到了，ACM队组织大家去登山观光，队员们发现山上一共有 $N$ 个景点，并且决定按照顺序来浏览这些景点，即每次所浏览景点的编号都要大于前一个浏览景点的编号。

同时队员们还有另一个登山习惯，就是不连续浏览海拔相同的两个景点，并且一旦开始下山，就不再向上走了。

队员们希望在满足上面条件的同时，尽可能多的浏览景点，你能帮他们找出最多可能浏览的景点数么？

输入格式：
第一行包含整数 $N$ ，表示景点数量。

第二行包含 $N$ 个整数，表示每个景点的海拔。

输出格式：
输出一个整数，表示最多能浏览的景点数。

数据范围：
$2 \leq N \leq 1000$

输入样例：

8
186 186 150 200 160 130 197 220

输出样例：

代码实现

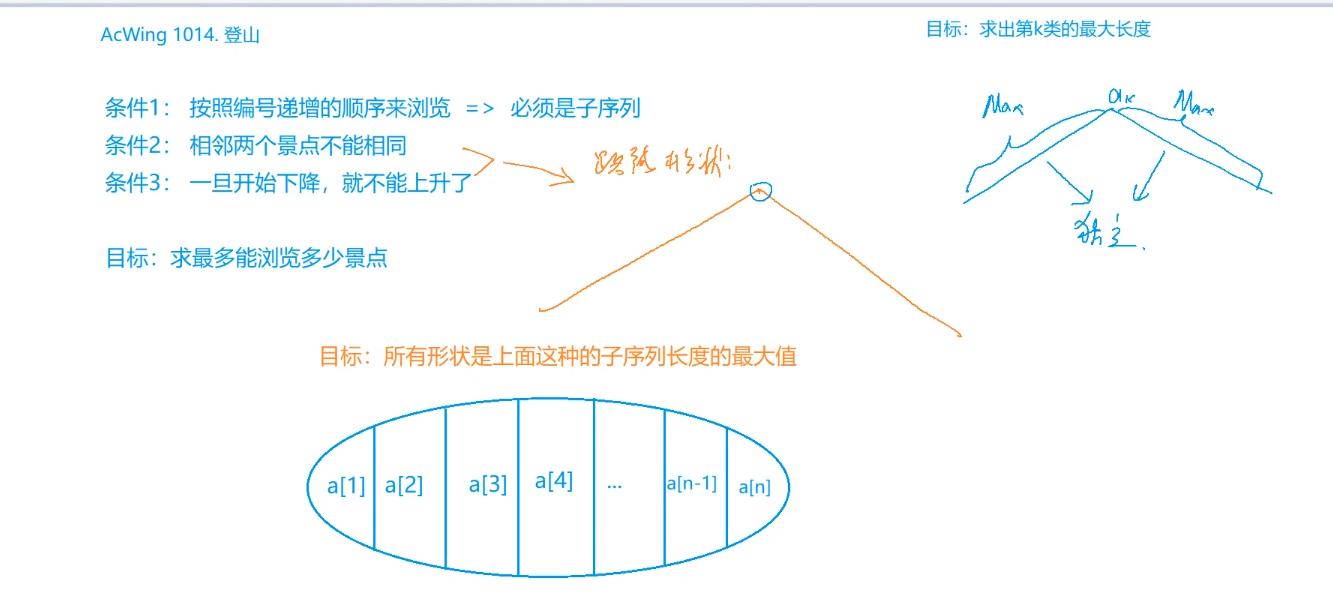
在这里插入图片描述
同理正反序进行最长上升子序列计算

$O(n^2)$

import sys
input = sys.stdin.readline

n = int(input().strip())
nums = list(map(int, input().strip().split()))
pre, suf = [1] * n, [1] * n
for i in range(n):
    pre[i] += max((pre[j] for j in range(i) if nums[i] > nums[j]), default=0)
    suf[n - 1 - i] += max((suf[n - 1 - j] for j in range(i) if nums[n - 1 - i] > nums[n - 1 - j]), default=0)

print(max(pre[i] + suf[i] for i in range(n)) - 1)

$O (n l o g n)$

import sys
from bisect import bisect_left
input = sys.stdin.readline

n = int(input().strip())
nums = list(map(int, input().strip().split()))

pre, suf, tmp1, tmp2 = [0] * n, [0] * n, [], []
for i in range(n):
    if tmp1 and tmp1[-1] >= nums[i]:
        idx = bisect_left(tmp1, nums[i])
        pre[i] = idx + 1
        tmp1[idx] = nums[i]
    else:
        tmp1.append(nums[i])
        pre[i] = len(tmp1)

    if tmp2 and tmp2[-1] >= nums[n - 1 - i]:
        idx = bisect_left(tmp2, nums[n - 1 - i])
        suf[n - 1 - i] = idx + 1
        tmp2[idx] = nums[n - 1 - i]
    else:
        tmp2.append(nums[n - 1 - i])
        suf[n - 1 - i] = len(tmp2)

print(max(pre[i] + suf[i] for i in range(n)) - 1)

合唱队形

题目描述：
$N$ 位同学站成一排，音乐老师要请其中的 $(N - K)$ 位同学出列，使得剩下的 $K$ 位同学排成合唱队形。合唱队形是指这样的一种队形：设 $K$ 位同学从左到右依次编号为 $1, 2, \dots, K$ ，他们的身高分别为 $T_1, T_2, …, T_K$ ，则他们的身高满足 $T_1<…<T_i>T_{i+1}>…>T_K(1≤i≤K)$ 。

你的任务是，已知所有 $N$ 位同学的身高，计算最少需要几位同学出列，可以使得剩下的同学排成合唱队形。

输入格式：

输入的第一行是一个整数 $N$ ，表示同学的总数。

第二行有 $N$ 个整数，用空格分隔，第 $i$ 个整数 $T_i$ 是第 $i$ 位同学的身高(厘米)。

输出格式：

输出包括一行，这一行只包含一个整数，就是最少需要几位同学出列。

数据范围：

$2 \leq N \leq 100$
$130≤T_i≤230$

输入样例：

8
186 186 150 200 160 130 197 220

输出样例：

代码实现

与上题一样的思路

$O(n^2)$

import sys
input = sys.stdin.readline

n = int(input().strip())
nums = list(map(int, input().strip().split()))

pre, suf = [1] * n, [1] * n

for i in range(n):
    pre[i] += max((pre[j] for j in range(i) if nums[i] > nums[j]), default=0)
    suf[n - 1 - i] += max((suf[n - 1 - j] for j in range(i) if nums[n - 1 - i] > nums[n - 1 - j]), default=0)

print(n - max(pre[i] + suf[i] for i in range(n)) + 1)

$O (n l o g n)$

import sys
from bisect import bisect_left
input = sys.stdin.readline

n = int(input().strip())
nums = list(map(int, input().strip().split()))

pre, suf, tmp1, tmp2 = [0] * n, [0] * n, [], []
for i in range(n):
    if tmp1 and tmp1[-1] >= nums[i]:
        idx = bisect_left(tmp1, nums[i])
        pre[i] = idx + 1
        tmp1[idx] = nums[i]
    else:
        tmp1.append(nums[i])
        pre[i] = len(tmp1)

    if tmp2 and tmp2[-1] >= nums[n - 1 - i]:
        idx = bisect_left(tmp2, nums[n - 1 - i])
        suf[n - 1 - i] = idx + 1
        tmp2[idx] = nums[n - 1 - i]
    else:
        tmp2.append(nums[n - 1 - i])
        suf[n - 1 - i] = len(tmp2)

print(n - max(pre[i] + suf[i] for i in range(n)) + 1)

友好城市

题目描述：
$P a l mia$ 国有一条横贯东西的大河，河有笔直的南北两岸，岸上各有位置各不相同的 $N$ 个城市。

北岸的每个城市有且仅有一个友好城市在南岸，而且不同城市的友好城市不相同。

每对友好城市都向政府申请在河上开辟一条直线航道连接两个城市，但是由于河上雾太大，政府决定避免任意两条航道交叉，以避免事故。

编程帮助政府做出一些批准和拒绝申请的决定，使得在保证任意两条航线不相交的情况下，被批准的申请尽量多。

输入格式：
第 $1$ 行，一个整数 $N$ ，表示城市数。

第 $2$ 行，到第 $n + 1$ 行，每行两个整数，中间用 $1$ 个空格隔开，分别表示南岸和北岸的一对友好城市的坐标。

输出格式：
仅一行，输出一个整数，表示政府所能批准的最多申请数。

数据范围：
$1≤N≤5000, 0≤x_i≤10000$

输入样例：

输出样例：

问题分析

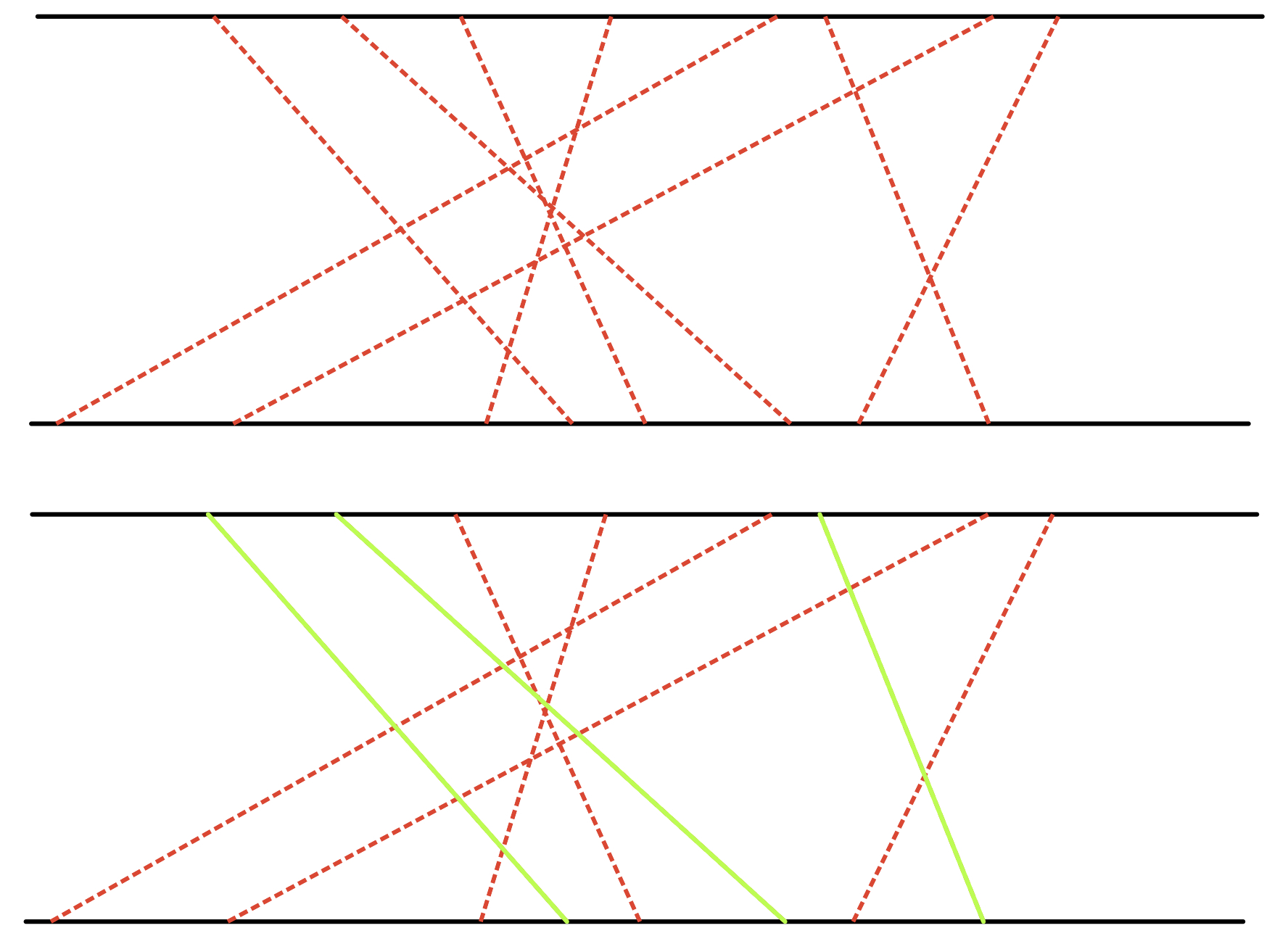
在这里插入图片描述
两对城市 $x_1,y_1),(x_2,y_2)$ 满足下面条件才会造成交叉：

$\large \left\{\begin{matrix} x_1 \geq x_2 \ \&\& \ y_1 \geq y_2 & \\ x_1 \leq x_2 \ \&\& \ y_1 \leq y_2 & \end{matrix}\right.$

要比较两端位置变量的大小关系，可以先对一边的端点进行排序，然后对排序的端点遍历，解决了一个端点的大小关系比较，接下来只用对另一个端点的大小关系进行比较就行了，相当于求另一个端点的最长上升子序列。

代码实现

$O(n^2)$

import sys
input = sys.stdin.readline

n = int(input().strip())
nums = sorted([tuple(map(int, input().strip().split())) for i in range(n)])
f = [1] * n

for i, (_, x) in enumerate(nums):
    f[i] += max((f[j] for j in range(i) if nums[j][1] < x), default=0)
print(max(f))

$O (n l o g n)$

import sys
input = sys.stdin.readline
from bisect import bisect_left

n = int(input().strip())
nums = sorted([tuple(map(int, input().strip().split())) for i in range(n)])

tmp = []
for i, (_, x) in enumerate(nums):
    if tmp and tmp[-1] >= x:
        tmp[bisect_left(tmp, x)] = x
    else:
        tmp.append(x)
print(len(tmp))

最大上升子序列和

题目描述：
一个数的序列 $b_i$ ，当 $b_1 < b_2 < ... < b_S$ 的时候，我们称这个序列是上升的。

对于给定的一个序列 $a_1, a_2, ..., a_N)$ ，我们可以得到一些上升的子序列 $a_{i_1}, a_{i_2}, ..., a_{i_K})$ ，这里 $1 ≤ i_1 < i_2 < ... < i_K ≤ N$ 。

比如，对于序列 $(1, 7, 3, 5, 9, 4, 8)$ ，有它的一些上升子序列，如 $(1, 7), (3, 4, 8)$ 等等。

这些子序列中和最大为 $18$ ，为子序列 $(1, 3, 5, 9)$ 的和。

你的任务，就是对于给定的序列，求出最大上升子序列和。

注意: 最长的上升子序列的和不一定是最大的，比如序列 $(100, 1, 2, 3)$ 的最大上升子序列和为 $100$ ，而最长上升子序列为 $(1, 2, 3)$ 。

输入格式：
输入的第一行是序列的长度 $N$ 。

第二行给出序列中的 $N$ 个整数，这些整数的取值范围都在 $0$ 到 $10000$ (可能重复)。

输出格式：
输出一个整数，表示最大上升子序列和。

数据范围：
$1 \leq N \leq 1000$

输入样例：

7
1 7 3 5 9 4 8

输出样例：

代码实现

从长度换成了总和，朴素动态规划一样的做法。

在此 贪心 + 二分 不好用，贪心二分替换数组后得重新计算一次总和，复杂度可能达到 $O(n^2logn)$ 。

import sys
input = sys.stdin.readline

n = int(input().strip())
nums = list(map(int, input().strip().split()))

# O(n ^ 2)
f = nums.copy()
for i in range(n):
    f[i] += max((f[j] for j in range(i) if nums[i] > nums[j]), default=0)
print(max(f))

*拦截导弹

题目描述：

某国为了防御敌国的导弹袭击，发展出一种导弹拦截系统。

但是这种导弹拦截系统有一个缺陷：虽然它的第一发炮弹能够到达任意的高度，但是以后每一发炮弹都不能高于前一发的高度。

某天，雷达捕捉到敌国的导弹来袭。

由于该系统还在试用阶段，所以只有一套系统，因此有可能不能拦截所有的导弹。

输入导弹依次飞来的高度（雷达给出的高度数据是不大于 $30000$ 的正整数，导弹数不超过 $1000$ ），计算这套系统最多能拦截多少导弹，如果要拦截所有导弹最少要配备多少套这种导弹拦截系统。

输入格式：

共一行，输入导弹依次飞来的高度。

输出格式：

第一行包含一个整数，表示最多能拦截的导弹数。

第二行包含一个整数，表示要拦截所有导弹最少要配备的系统数。

数据范围：

雷达给出的高度数据是不大于 $30000$ 的正整数，导弹数不超过 $1000$ 。

输入样例：

389 207 155 300 299 170 158 65

输出样例：

6
2

问题分析

最多拦截多少个导弹?（动态规划）
经典LIS问题，直接模板解决。

需要多少套拦截系统?（贪心）

遍历当前元素有两种操作：

接在现有的某个子序列之后
创建一个新的子序列

先用直觉猜一个做法，保持当前子序列的末尾尽可能的大，因为末尾越大越可能接上其他元素。反过来思考，对当前元素进行操作时，选取末尾尽可能接近当前元素的前面子序列。

在这里插入图片描述

代码实现

import sys
from bisect import bisect_left

input = sys.stdin.readline

nums = list(map(int, input().strip().split()))

# 第一问
tmp = []
for i, x in enumerate(nums):
    if tmp and tmp[-1] < x:
        l, r = 0, len(tmp)
        while l < r:
            mid = (l + r) // 2
            if tmp[mid] <= x:
                r = mid
            else:
                l = mid + 1
        tmp[l] = x
    else:
        tmp.append(x)

print(len(tmp))

# 第二问
tmp.clear()
for x in nums:
    idx = bisect_left(tmp, x)
    if idx >= len(tmp):
        tmp.append(x)
    else:
        tmp[idx] = x
print(len(tmp))

扩展

Dilworth 定理

把序列分成不升子序列的最少个数，等于序列的最长上升子序列长度
把序列分成不降子序列的最少个数，等于序列的最长下降子序列长度

*导弹防御系统

题目描述：

为了对抗附近恶意国家的威胁， $R$ 国更新了他们的导弹防御系统。

一套防御系统的导弹拦截高度要么一直 严格单调 上升，要么一直 严格单调 下降。

例如，一套系统先后拦截了高度为 $3$ 和高度为 $4$ 的两发导弹，那么接下来该系统就只能拦截高度大于4的导弹。

给定即将袭来的一系列导弹的高度，请你求出 至少需要多少套防御系统，就可以将它们全部击落。

输入格式：

输入包含多组测试用例。

对于每个测试用例，第一行包含整数 $n$ ，表示来袭导弹数量。

第二行包含 $n$ 个不同的整数，表示每个导弹的高度。

当输入测试用例 $n = 0$ 时，表示输入终止，且该用例无需处理。

输出格式：

对于每个测试用例，输出一个占据一行的整数，表示所需的防御系统数量。

数据范围：

$1 \leq n \leq 50$

输入样例：

5
3 5 2 4 1
0

输出样例：

问题分析

由于导弹拦截高度要么一直上升要么一直下降，所以不能直接使用上一题的结论。

因此采用暴力枚举，问题为当前元素放在上升序列里还是下降序列里，采用上一题贪心的思想，若放到上升序列里，一定放在最后一个元素最大的子序列里，放到下降序列里也同理。

代码实现

import sys
input = sys.stdin.readline
from bisect import bisect_left

while (True):
    n = int(input().strip())
    if not n:
        break
    nums = list(map(int, input().strip().split()))
    ans = 0x3f3f3f3f
    up, down = [0] * n, [0] * n


    def dfs(total, cnt_up, cnt_down):
        global ans
        if cnt_up + cnt_down >= ans:
            return
        if total == n:
            ans = min(ans, cnt_up + cnt_down)
            return

        # 插入上升子序列
        if cnt_up and up[cnt_up - 1] >= nums[total]:
            idx = bisect_left(up, nums[total], 0, cnt_up)
            tmp, up[idx] = up[idx], nums[total]
            dfs(total + 1, cnt_up, cnt_down)
            up[idx] = tmp
        else:
            up[cnt_up] = nums[total]
            dfs(total + 1, cnt_up + 1, cnt_down)

        # 插入下降子序列
        if cnt_down and down[cnt_down - 1] <= nums[total]:
            l, r = 0, cnt_down
            while l < r:
                mid = (l + r) // 2
                if down[mid] <= nums[total]:
                    r = mid
                else:
                    l = mid + 1
            tmp, down[l] = down[l], nums[total]
            dfs(total + 1, cnt_up, cnt_down)
            down[l] = tmp
        else:
            down[cnt_down] = nums[total]
            dfs(total + 1, cnt_up, cnt_down + 1)

    dfs(0, 0, 0)
    print(ans)

*最长公共上升子序列

题目描述：

熊大妈的奶牛在小沐沐的熏陶下开始研究信息题目。

小沐沐先让奶牛研究了最长上升子序列，再让他们研究了最长公共子序列，现在又让他们研究 最长公共上升子序列 了。

小沐沐说，对于两个数列 $A$ 和 $B$ ，如果它们都包含一段位置不一定连续的数，且数值是严格递增的，那么称这一段数是两个数列的公共上升子序列，而所有的公共上升子序列中最长的就是最长公共上升子序列了。

奶牛半懂不懂，小沐沐要你来告诉奶牛什么是最长公共上升子序列。

不过，只要告诉奶牛它的长度就可以了。

数列 $A$ 和 $B$ 的长度均不超过 $3000$ 。

输入格式：

第一行包含一个整数 $N$ ，表示数列 $A ， B$ 的长度。

第二行包含 $N$ 个整数，表示数列 $A$ 。

第三行包含 $N$ 个整数，表示数列 $B$ 。

输出格式：

输出一个整数，表示最长公共上升子序列的长度。

数据范围：

$1 \leq N \leq 3000$ ，序列中的数字均不超过 $2^31−1$ 。

输入样例：

4
2 2 1 3
2 1 2 3

输出样例：

问题分析

LIS(最长上升子序列，Longest Increasing Subsequence)
LCS(最长公共子序列，Longest Common Subsequence)
LCIS(最长公共上升子序列，Longest Common Increasing Subsequence)

状态表示
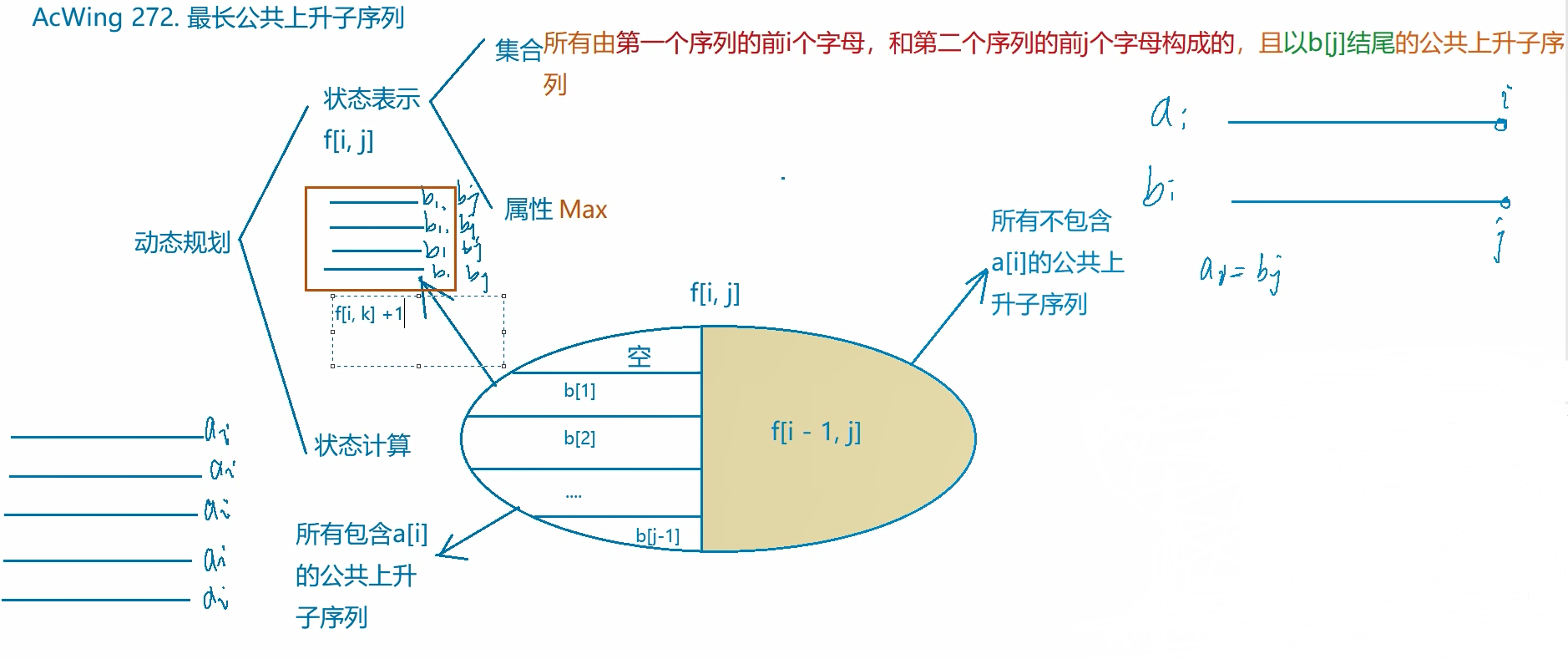
在这里插入图片描述

代码实现

$O(n^3)$

import sys

input = sys.stdin.readline
n = int(input().strip())
a = list(map(int, input().strip().split()))
b = list(map(int, input().strip().split()))

f = [[0] * (n + 1) for _ in range(n + 1)]

for i in range(n):
    for j in range(n):
        f[i + 1][j + 1] = f[i][j + 1]
        if a[i] != b[j]:
            continue
        mx = max((f[i][k + 1] for k in range(j) if b[j] > b[k]), default=0) + 1
        f[i + 1][j + 1] = max(f[i + 1][j + 1], mx)
print(max(f[-1][i] for i in range(1, n + 1)))

$O(n^2)$
用一个变量，存储上一个阶段的能够接在 $a [i]$ 前面的最大的状态值。

import sys
input = sys.stdin.readline

n = int(input().strip())
a = list(map(int, input().strip().split()))
b = list(map(int, input().strip().split()))

f = [[0] * (n + 1) for _ in range(n + 1)]

for i in range(n):
    mx = 1
    for j in range(n):
        f[i + 1][j + 1] = f[i][j + 1]
        if a[i] == b[j]:
            f[i + 1][j + 1] = max(f[i + 1][j + 1], mx)
        if j and a[i] > b[j - 1]:
            mx = max(mx, f[i][j] + 1)
print(max(f[-1][i] for i in range(1, n + 1)))