前言

  学习资料来自 C训练以及CSDN各博主的博客整合而来，内容涵盖计算机通识内容：进制转换、信息单位、数据校验、多媒体基础参数、HTTP \ HTTPS协议、OSI七层模型、IP基础 \ IPv6、网络拓扑机构、域名解析、常用网络命令和端口、数据结构常识等内容，合计11篇内容。

  笔记整理不易，记得观看后，一键三联！！！

1、进制的定义

  数制：也称为计数制，是一种计数的方法，是用一组固定的符号和统一的规则来表示数值的方法。在计数过程中采用进位的方法称为进位计数制（进制），包括数位、基数和位权三个要素。

• 数位：指数字符号在一个数中所处的位置。
• 基数：指在某种进位计数制中数位上所能使用的数字符号的个数。例如十进制的基数为10
• 位权：数制中某一位上的1所表示数值的大小（所处位置的价值）。例如十进制的230，1的位权是100，2的位权是10，3的位权是1

  二进制：是指在数学和数字电路中以2为基数的记数系统，二进制只有0和1两个数字符号，其运算规律是逢2进1，例如101101。为了与其他进制区别，二进制数的后缀都用大写字母B，例如101101B

  八进制：一种以8为基数的计数法，采用0，1，2，3，4，5，6，7这八个数字符号，其运算规律是逢8进1，例如77。为了与其他进制区别，八进制数的后缀都用大写字母O（不是数字0），例如77O

  十进制：一种以10为基数的计数法，采用0，1，2，3，4，5，6，7，8，9这十个数字符号，其运算规律是逢10进1，例如88。为了与其他进制区别，十进制数的后缀都用大写字母D，例如88D

  十六进制：一种以16为基数的计数法，采用0，1，2，3，4，5，6，7，8，9，A，B，C，D，E，F这十六个数字和字母符号，其运算规律是逢16进1，例如9527。为了与其他进制区别，十六进制数的后缀都用大写字母H，例如9527H

2、各进制间的转换方法

2.1 二进制的转换

• 二进制转换十进制

  采用位置计数法，其位权是以2为底的幂，顺序从右到左，从0开始计数。例如：

$$11011B=1\ast 23+0\ast 22+1\ast 21+1\ast 20=11D$$

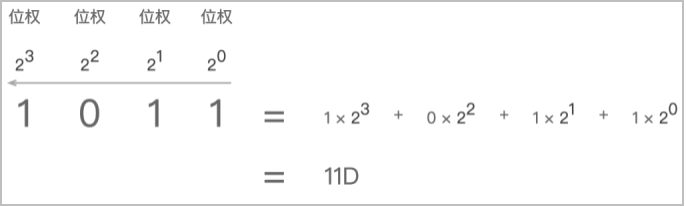
• 二进制转八进制

  采用三合一法，即从二进制的小数点为分界点，向左（或向右）每三位对应八进制的一位，不足三位的前面补0，例如：
$$110110011B=(0)10110011=263O$$

• 二进制转十六进制

  采用四合一法，即从二进制的小数点为分界点，向左（或向右）每四位对应十六进制的一位，不足四位的前面补0，例如：
$$10110011B=10110011=B3H$$

2.2 八进制的转换

• 八进制转换二进制

  采用位置计数法，其位权是以2为底的幂，顺序从右到左，从0开始计数。例如：

$$11011B=1\ast 23+0\ast 22+1\ast 21+1\ast 20=11D$$

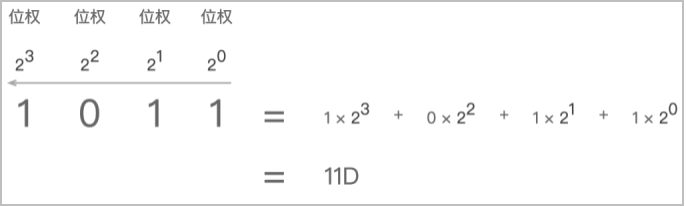
• 八进制转十进制

  采用三合一法，即从二进制的小数点为分界点，向左（或向右）每三位对应八进制的一位，不足三位的前面补0，例如：
$$110110011B=(0)10110011=263O$$

• 八进制转十六进制

  采用四合一法，即从二进制的小数点为分界点，向左（或向右）每四位对应十六进制的一位，不足四位的前面补0，例如：
$$10110011B=10110011=B3H$$

2.3 十进制的转换

• 十进制转换二进制

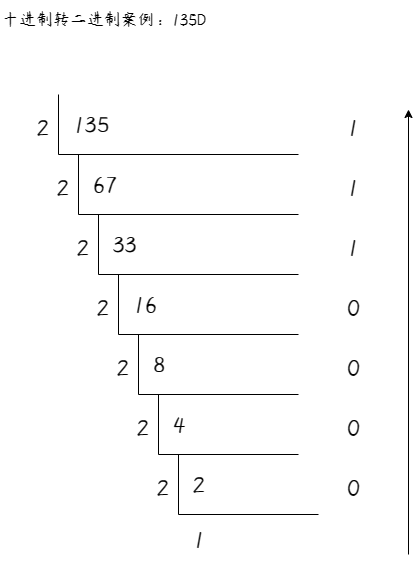
  整数采用“除2倒取余”，小数采用“乘2取整”。例如十进制数135D转换成二进制时，将135除以2，得余数，直到不能整除，然后再将余数从下至上倒取，结果为10000111B

$$\begin{gathered} 135D=135/2⟹1 \\ =67/2⟹1 \\ =33/2⟹1 \\ =16/2⟹0 \\ =8/2⟹0 \\ =4/2⟹0 \\ =2/2⟹0 \\ =1 \end{gathered}$$

• 十进制转八进制

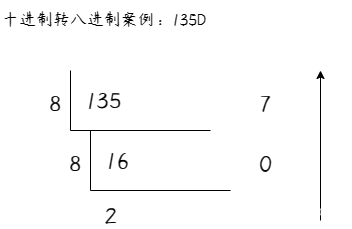
  和转二进制的方法类似，整数采用“除8倒取余”，小数采用“乘8取整”。例如十进制数135D转换成八进制时，将10除以8，得余数，直到不能整除，然后再将余数从下至上倒取，结果为207O
$$\begin{gathered} 135D=135/8⟹7 \\ =16/8⟹0 \\ =2 \end{gathered}$$

• 十进制转十六进制

  采用“除16倒取余”，小数采用“乘16取整”，例如：135D=87H
$$\begin{gathered} 135D=135/16⟹7 \\ =8 \end{gathered}$$

2.4 十六进制的转换

• 十六进制转换二进制

  与二进制转十六进制的方法相反，采用四合一法，例如：
$$B3H=10110011=10110011B$$

• 十六进制转八进制
    不能直接转换，需要先转成二进制，再将二进制转成八进制
• 十六进制转十进制
    与二进制转十进制的方法一样，采用位置计数法，其位权是以16为底的幂，顺序从右到左，从0开始计数。例如：
  $$26H=2\ast 161+6\ast 160=38D$$
  

3、进制转换表

以十进制的前17个数与二进制、八进制、十六进制对应关系：

十进制	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
二进制	0	1	10	11	100	101	110	111	1000	1001	10010	1011	1100	1101	1110	1111	10000
八进制	0	1	2	3	4	5	6	7	8	10	11	12	13	14	15	16	17
十六进制	0	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F	10

4、练习题

1.二进制数10110B与十进制数78D相加，最后再将结果转换为十六进制数，那么这个十六进制数是______H？

  解题思路： 先把78D转换成二进制，78D=1001110B，再把两个二进制数相加 10110B+1001110B=1100100B，四位合一，为十六进制，故此64H

  答案：64H

2.二进制数 111100000001001 转十六进制数的结果是______H

  解题思路： 二进制转为十进制后再转十六进制，或者直接使用二进制(B)转十六进制（H）：从右往左，四位一看。不够往前面补充 0。参考下图四位对齐，填写对应数字7809

  答案：7809H

资料来源

  感谢大佬们的资料!!! 参考资料文献来源如下。

• C训练 IT技能训练平台
• 进制的概念与转换（二进制、十进制、八进制、十六进制）——琴酒3