1--核心代码

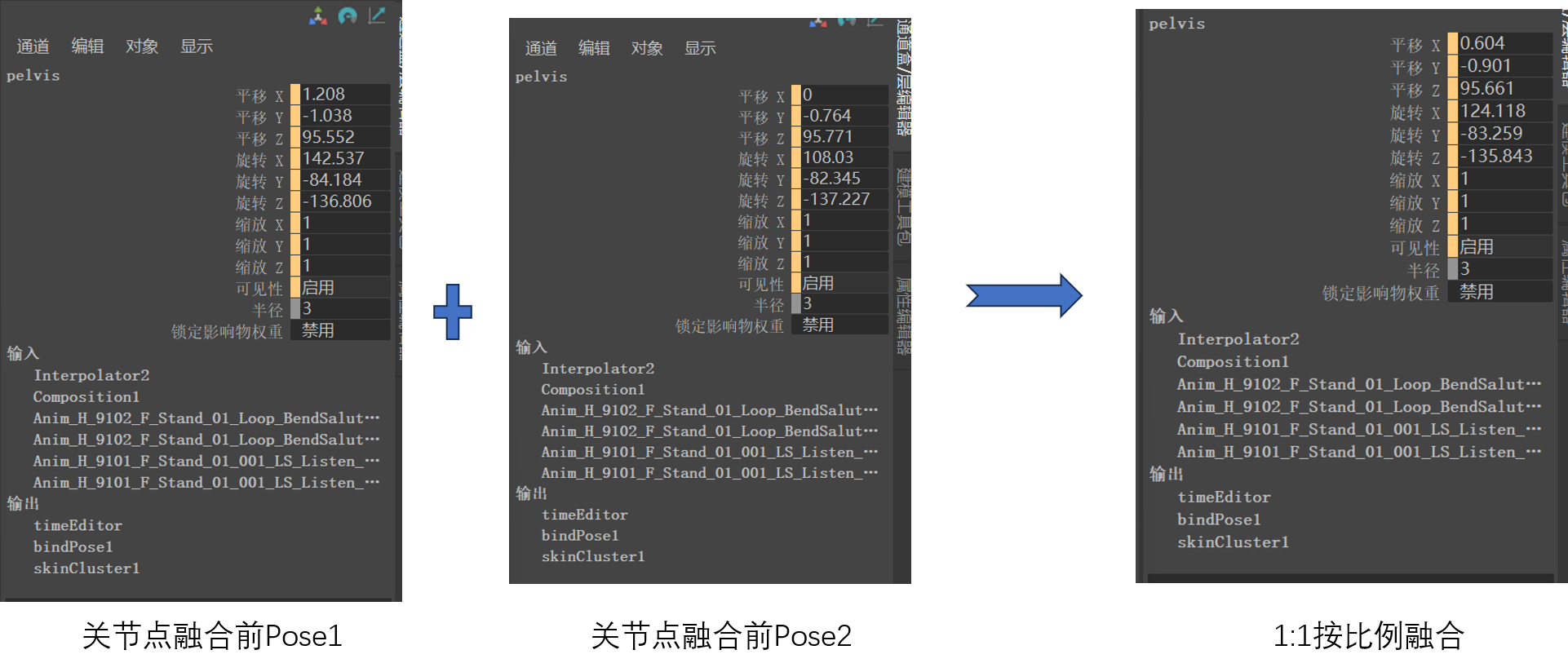
        6D位姿一般指平移向量和旋转向量，Maya软件中关节点的6D位姿指的是相对平移向量和欧拉旋转向量；

        为了按比例融合两个Pose，首先需要将欧拉旋转向量转换为旋转矩阵，在将旋转矩阵转换为四元数，利用球面线性插值实现Pose的融合，融合后的四元数需要重新转换为欧拉旋转向量，整个流程如下：欧拉旋转向量→旋转矩阵→四元数→球面线性插值→旋转矩阵→欧拉旋转向量；

'''
@File    :   fusion6DPose.py
@Time    :   2024/03/14 17:08:00
@Author  :   Jinfu Liu
@Version :   1.0 
@Desc    :   fusion 6DPose between two motion
'''
import numpy as np
from scipy.spatial.transform import Rotation
from pyquaternion import Quaternion

def fusion6DPose(pose1:np.ndarray, pose2:np.ndarray, rate:float) -> np.ndarray:
    '''
    按比例融合平移向量和欧拉旋转向量
    '''
    assert pose1.shape[0] == pose2.shape[0]
    return_pose = np.zeros_like(pose1) # [num_joint, 6]
    for joint_idx in range(pose1.shape[0]): # 遍历处理所有关节点
        T1 = pose1[joint_idx][:3] # 平移向量
        R1 = pose1[joint_idx][3:] # 欧拉旋转
        T2 = pose2[joint_idx][:3] # 平移向量
        R2 = pose2[joint_idx][3:] # 欧拉旋转
        
        R1 = Rotation.from_euler('xyz', list(R1), degrees=True).as_matrix() # 欧拉角->旋转矩阵
        R2 = Rotation.from_euler('xyz', list(R2), degrees=True).as_matrix()
        
        T3 = rate * T1 + (1 - rate) * T2
        Q1 = Rotation.from_matrix(R1).as_quat() # 旋转矩阵->四元数
        Q2 = Rotation.from_matrix(R2).as_quat()
        Q3 = Quaternion.slerp(Quaternion(Q1), Quaternion(Q2), 1-rate) # 球面线性插值
        R3 = Rotation.from_quat(Q3.elements).as_matrix() # 四元数->旋转矩阵
        R3 = Rotation.from_matrix(R3).as_euler('xyz', degrees = True) # 旋转矩阵->欧拉角
        return_pose[joint_idx][:3] = T3
        return_pose[joint_idx][3:] = R3
    
    return return_pose

if __name__ == "__main__":
    # 关节点的6D位姿
    pose1 = np.array([[1.208, -1.038, 95.552, 142.537, -84.184, -136.806]]) # Tx, Ty, Tz, Rx, Ry, Rz
    
    # 关节点的6D位姿
    pose2 = np.array([[0, -0.764, 95.771, -71.97, -97.655, 42.773]]) # Tx, Ty, Tz, Rx, Ry, Rz

    # 融合比例
    alpha = 0.5

    # 计算融合后的刚体C的6D位姿
    # Pose3 = rate * pose1 + (1 - rate) * Pose2
    Pose3 = fusion6DPose(pose1, pose2, alpha) # 这里只用一个关节点进行测试

    # 融合后
    print("PoseC: ", Pose3) # [[0.604, -0.901, 95.6615, 124.11717241, -83.2593501, -135.84186147]]
    print("All done!")

2--Maya验证