寒假作业Day 11

news2024/11/18 6:41:07

寒假作业Day 11

一、选择题

在这里插入图片描述

栈满的判断：在链式存储结构中，栈的大小是动态的，只受限于系统分配给程序的内存大小。因此，理论上，链式栈不会因为空间不足而“满”。所以，不需要判断栈满。
栈空的判断：链式栈通常有一个指针指向栈顶元素。如果这个指针是NULL或者指向某个表示空栈的特殊节点，那么我们可以判断栈是空的。因此，需要判断栈空。

在这里插入图片描述

这里画图操作，p->q->…这样的一个样式，让p的后继指针指向原本q指向的地方，再把q free掉其实就可以了

在这里插入图片描述

A：随机存取是顺序表的优点，B很明显也是错误的，结构体里面不仅有元素值，还有指针，不可能花费的存储空间更少；C是对的，顺序表插入删除都需要移动元素，而链表只需要控制指针即可；D：链表的物理顺序是随机摆放的，并不与其逻辑顺序相同

在这里插入图片描述

队列是一种既可以插入，又可以删除，先进先出的线性表

在这里插入图片描述

A. 通常不会出现栈满的情况
解释：
顺序栈是基于数组实现的，它的大小在创建时就已经确定，当栈中元素数量达到数组的最大容量时，就会出现栈满的情况。而链栈是基于链表实现的，链表的大小是动态的，可以随着元素的插入而增长，因此链栈通常不会出现栈满的情况。

其他选项的解释：
B. 通常不会出现栈空的情况 - 无论是顺序栈还是链栈，当栈中没有元素时，都会处于栈空的状态。因此，这个选项不是链栈相对于顺序栈的优势。

C. 插入操作更容易实现 - 无论是顺序栈还是链栈，插入操作（即入栈操作）的复杂度都是O(1)，因为都是将新元素放在栈顶。因此，这个选项不是链栈相对于顺序栈的优势。

D. 删除操作更容易实现 - 无论是顺序栈还是链栈，删除操作（即出栈操作）的复杂度也都是O(1)，因为都是从栈顶删除元素。因此，这个选项也不是链栈相对于顺序栈的优势。

二、编程题

在这里插入图片描述

// 全局变量，用于在reverse函数递归调用时存储下一个要处理的节点  
struct ListNode * next = NULL;  
 
struct ListNode * reverse(struct ListNode * head, int n)  
{  
    // 如果n为1，说明只需要反转一个节点，此时直接返回该节点  
    if(n == 1)  
    {  
        // 保存当前节点的下一个节点  
        next = head->next;  
        return head;  
    }  
      
    // 递归调用reverse函数，反转head的下一个节点开始的n-1个节点  
    struct ListNode * newHead = NULL;  
    newHead = reverse(head->next, n-1);  
      
    // 将当前节点的下一个节点的next指针指向当前节点，实现反转  
    head->next->next = head;  
      
    // 将当前节点的next指针指向tmp，即原来head的下一个节点的下一个节点  
    head->next = next;  
      
    // 返回新的头节点  
    return newHead;  
}  
  
struct ListNode* reverseBetween(struct ListNode* head, int m, int n ) {  
    // 如果m为1，说明从链表的头节点开始反转，直接调用reverse函数  
    if(m == 1)  
    {  
        return reverse(head, n);  
    }  
      
    // 递归调用reverseBetween函数，处理head的下一个节点开始的子链表  
    struct ListNode * reversePart = NULL;  
    reversePart = reverseBetween(head->next, m-1, n-1);  
      
    // 将当前节点的next指针指向反转后的子链表头节点  
    head->next = reversePart;  
      
    // 返回头节点，此时头节点没有变化  
    return head;  
}

这里我们使用的是递归，所以会比较复杂，我们拿例子来演示一下！

*1->2->3->4->5->NULL
*变成1->4->3->2->5->NULL

*首先我们看reverseBetween函数，如果m==1，我们就直接调用reverse辅助函数，反转链表；但一开始我们的m=2，所以我们会从下面开始：
reversePart=reverseBetween函数递归后返回的结果，并让head->next指向reversePart
*我们递归一次，m=1，n=3，符合条件，走入reverse辅助函数
又因为n=3，所以在其中递归两次，让n=1时才一步一步返回
*此时n=1，head指向的值是4，于是next存储的就是5的位置，返回head，也就是4的位置，并且由于next是全局变量，所以值并没有随着递归的返回而销毁，而是保留（后面的next指针一直没有变过，一直都在5的位置上）
*reverse函数返回到n=2的时候，此时newHead指向4（由于我们会发现在递归中，newHead的值并未发生改变，所以其也一直指向4）；之前n=1的时候head指向4，所以此时n=2的head指向的是3，3的next是4，所以让4的next指向3，并且让3的next指向5(next)
*此刻来到n=3的时候，newHead依旧为4，next依旧为5；此时head指向2，2的next为3，让3的next指向2，2的next指向5（next）
*此时reverse辅助函数的递归结束，我们开始看reverseBetween函数，返回了reverse（head，n）（m=1时），此时head指向2，n=3，也就是reverse函数返回给我们的newHead（4）；我们再次回到m=2，n=4的时候，这个时候head指向1，于是reversePart指向4，而head->next=4(1->4);而在刚才的reverse辅助函数中，我们让4指向3，3指向2，2指向5，即如图的形状，也就是成功完成了转变！

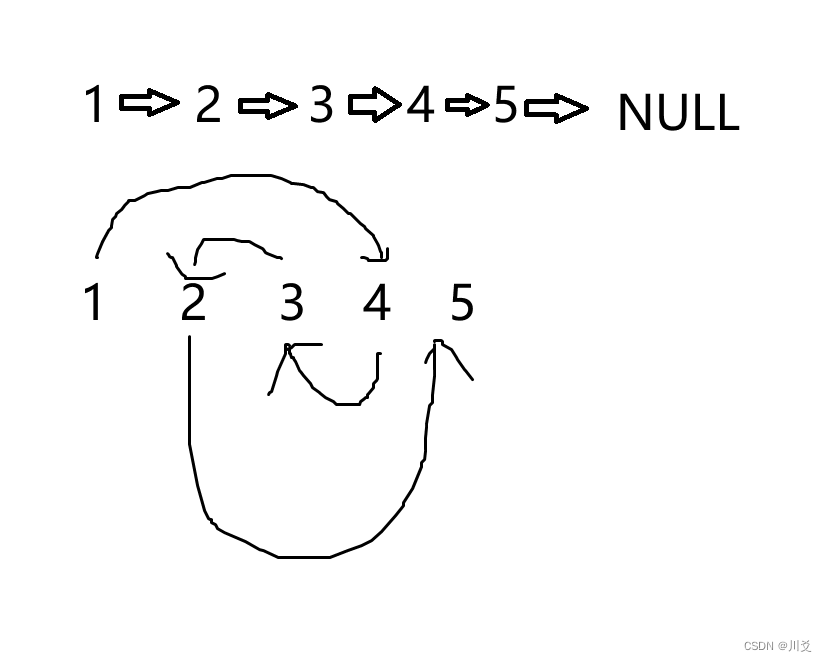
在这里插入图片描述

其实分析原理，我们会发现，首先我们是找到反转的tail，也就是m点，然后就开始进行reverse；在reverse中我们首先找到n点，然后用next记录下n点的next，并用newHead记录下n点的地址；reverse递归完之后，用m点的前一个节点连接n点；而在reverse中，我们将指针逐个反转，把几个特殊节点保留，是十分巧妙的思想

在这里插入图片描述

struct ListNode* removeZeroSumSublists(struct ListNode* head){
    struct ListNode*dummy=(struct ListNode*)malloc(sizeof(struct ListNode));//头节点可能会被消除，要建立一个虚拟头节点
    dummy->next=head;
    struct ListNode*p=dummy;
    struct ListNode*q=p->next;
    int x=0;
    while(p)//其实本质上是用了快慢指针的思想
    {
        x=0;//这里还是要更新的
        q=p->next;
        while(q)
        {
            x-=q->val;//用减号是一个真正的亮点(省去很多麻烦)
            if(x==0)
            {
                p->next=q->next;//删除节点
            }
            q=q->next;
        }
        p=p->next;
    }
    return dummy->next;
}

这里我们还是先举个例子，比如1，2，3，-3，4这个链表

*1->2->3->-3->4
*变成1->2->-4
*首先，创建一个哨兵位，让其next指向head，并让p指向哨兵位，q指向head，并创建一个x来存储val值
*首先套一个p指针的循环，x=0（更新值），q指向p->next
*之后走q的while循环，x减去此时q->val，然后如果x==0，也就是找到了总和值为0的点，就让p->next指向q->next，删除中间节点，并且每次都让q=q->next，这是遍历的必然要求
*在这里，我们会发现，q在指向1的时候，是明显无法让x==0的，所以此时p=p->next，也就是q指向2，这里也不行；只有当q指向3的时候，才可以，而此时p指向2，于是2->next变成了4，即现在的链表为1->2->4，之后p走到3，q走到4，由于后面没有总和值为0的节点，所以都是遍历完就结束了，最后返回哨兵位的next，也就是头节点