---

1.背景

2016年，Mirjalili受到蜻蜓静态和动态集群行为启发，提出了蜻蜓算法(Dragonfly algorithm, DA)。

2.算法原理

2.1算法思想

蜻蜓集群有两种行为目的：狩猎（静态集群）和迁徙（动态集群）。静态集群中，蜻蜓分成小群捕猎，局部移动和突然飞行路径变化是其特征。动态集群则是大量蜻蜓在单一方向上长距离迁徙。这两种行为类似于元启发式优化中的探索和开发利用阶段，静态集群探索不同区域，而动态集群利用大群体沿着一个方向飞行。

2.2算法过程

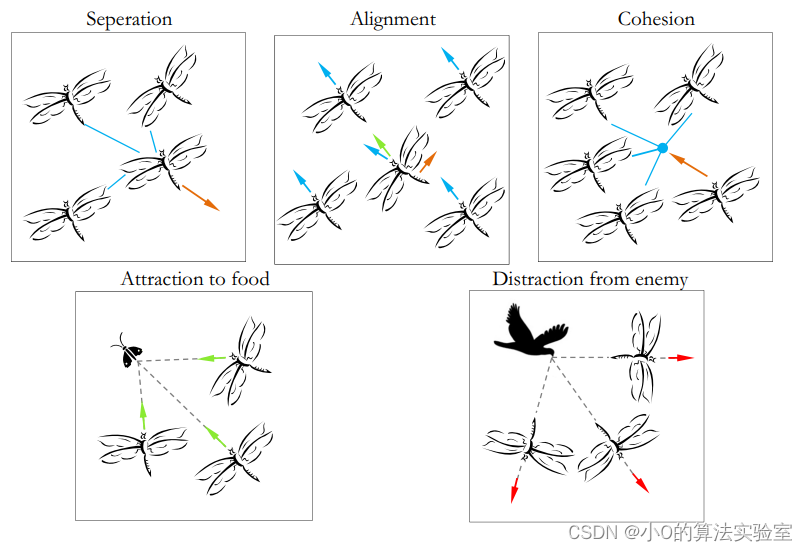
群体的行为遵循三个基本原则：

• 分离（Separation）：指个体在邻域内静态地避免与其他个体碰撞
• 对齐（Alignment）：表示个体的速度与邻域内其他个体的速度匹配
• 凝聚（Cohesion）：指个体朝向邻域质心的趋势
  分离：
  $$S_i=-\sum _{j=1}^N{X}_i-X_j$$
  其中，$X_j$表示第$i$只蜻蜓领域内其他蜻蜓，$S_i$表示第$i$只蜻蜓分离位置向量。
  对齐：
  $$A_i=\frac{{\sum }_{j=1}^N{V}_j}{N}$$
  其中，$A_i$表示第$i$只蜻蜓与领域内其他蜻蜓对齐的位置向量。
  凝聚：
  $$C_i=\frac{{\sum }_{j=1}^N{X}_j}{N}-X_i$$
  其中，$C_i$示第$i$只蜻蜓凝聚时的位置向量。
  寻找食物：
  $$F_i=X^{+}-X_i$$
  其中，$X^{+}$表示猎物位置。
  躲避天敌：
  $$E_i=X^{-}+X_i$$
  其中，$X^{-}$表示天敌位置。
  位置更新：
  $$\begin{gathered} \Delta X_{t+1}=(s{S}_i+a{A}_i+c{C}_i+f{F}_i+e{E}_i)+w\Delta X_t \\ {X}_{t+1}=X_t+\Delta X_{t+1} \end{gathered}$$
  式中参数均为权重因子。
  为了提高DA随机性和探索能力，当没有邻近解时，它们需要在搜索空间中进行Lévy飞行：
  $$X_{t+1}=X_t+\text{Leˊvy}(d)\times X_t$$
  Lévy函数表述如下（Mantegna算法）：
  $$\begin{gathered} \text{Leˊvy}(x)=0.01\times \frac{r_1\times \sigma }{|r_2{|}^{\frac{1}{\beta }}} \\ \sigma ={\left(\frac{\Gamma (1+\beta )\times \sin \left(\frac{\pi \beta }{2}\right)}{\Gamma \left(\frac{1+\beta }{2}\right)\times \beta \times 2^{\left(\frac{\beta -1}{2}\right)}}\right)}^{1/\beta } \end{gathered}$$
  伪代码：
  

3.代码实现

% 蜻蜓优化算法
function [Best_pos,Best_fitness,Iter_curve,History_pos, History_best]=DA(pop, dim, ub,lb, fobj, maxIter)
%input
%pop 种群数量
%dim 问题维数
%ub 变量上边界
%lb 变量下边界
%fobj 适应度函数
%maxIter 最大迭代次数
%output
%Best_pos 最优位置
%Best_fitness 最优适应度值
%Iter_curve 每代最优适应度值
%History_pos 每代种群位置
%History_best 每代最优个体位置
%% 记录
Iter_curve=zeros(1,maxIter);
r=(ub-lb)/10;
Delta_max=(ub-lb)/10;
Food_fitness=inf;
Food_pos=zeros(dim,1);
Enemy_fitness=-inf;
Enemy_pos=zeros(dim,1);
%% 初始化
X=initialization(pop,dim,ub,lb);
Fitness=zeros(1,pop);
DeltaX=initialization(pop,dim,ub,lb);
%% 迭代
for iter=1:maxIter
    
    r=(ub-lb)/4+((ub-lb)*(iter/maxIter)*2);
    
    w=0.9-iter*((0.9-0.4)/maxIter);
       
    my_c=0.1-iter*((0.1-0)/(maxIter/2));
    if my_c<0
        my_c=0;
    end
    
    s=2*rand*my_c; % Seperation weight
    a=2*rand*my_c; % Alignment weight
    c=2*rand*my_c; % Cohesion weight
    f=2*rand;      % Food attraction weight
    e=my_c;        % Enemy distraction weight
    
    for i=1:pop %Calculate all the objective values first
        Fitness(1,i)=fobj(X(:,i)');
        if Fitness(1,i)<Food_fitness
            Food_fitness=Fitness(1,i);
            Food_pos=X(:,i);
        end
        
        if Fitness(1,i)>Enemy_fitness
            if all(X(:,i)<ub') && all( X(:,i)>lb')
                Enemy_fitness=Fitness(1,i);
                Enemy_pos=X(:,i);
            end
        end
    end
    
    for i=1:pop
        index=0;
        neighbours_no=0;
        
        clear Neighbours_DeltaX
        clear Neighbours_X
        for j=1:pop
            Dist2Enemy=distance(X(:,i),X(:,j));
            if (all(Dist2Enemy<=r) && all(Dist2Enemy~=0))
                index=index+1;
                neighbours_no=neighbours_no+1;
                Neighbours_DeltaX(:,index)=DeltaX(:,j);
                Neighbours_X(:,index)=X(:,j);
            end
        end
        
        % 分离
        % Eq. (3.1)
        S=zeros(dim,1);
        if neighbours_no>1
            for k=1:neighbours_no
                S=S+(Neighbours_X(:,k)-X(:,i));
            end
            S=-S;
        else
            S=zeros(dim,1);
        end
        
        % 对齐
        % Eq. (3.2)
        if neighbours_no>1
            A=(sum(Neighbours_DeltaX')')/neighbours_no;
        else
            A=DeltaX(:,i);
        end
        
        % 凝聚
        % Eq. (3.3)
        if neighbours_no>1
            C_temp=(sum(Neighbours_X')')/neighbours_no;
        else
            C_temp=X(:,i);
        end
        
        C=C_temp-X(:,i);
        
        % 寻找食物
        % Eq. (3.4)
        Dist2Food=distance(X(:,i),Food_pos(:,1));
        if all(Dist2Food<=r)
            F=Food_pos-X(:,i);
        else
            F=0;
        end
        
        % 躲避天敌
        % Eq. (3.5)
        Dist2Enemy=distance(X(:,i),Enemy_pos(:,1));
        if all(Dist2Enemy<=r)
            Enemy=Enemy_pos+X(:,i);
        else
            Enemy=zeros(dim,1);
        end
        
        for tt=1:dim
            if X(tt,i)>ub(tt)
                X(tt,i)=lb(tt);
                DeltaX(tt,i)=rand;
            end
            if X(tt,i)<lb(tt)
                X(tt,i)=ub(tt);
                DeltaX(tt,i)=rand;
            end
        end
        
        if any(Dist2Food>r)
            if neighbours_no>1
                for j=1:dim
                    DeltaX(j,i)=w*DeltaX(j,i)+rand*A(j,1)+rand*C(j,1)+rand*S(j,1);
                    if DeltaX(j,i)>Delta_max(j)
                        DeltaX(j,i)=Delta_max(j);
                    end
                    if DeltaX(j,i)<-Delta_max(j)
                        DeltaX(j,i)=-Delta_max(j);
                    end
                    X(j,i)=X(j,i)+DeltaX(j,i);
                end
            else
                % Eq. (3.8)
                X(:,i)=X(:,i)+Levy(dim)'.*X(:,i);
                DeltaX(:,i)=0;
            end
        else
            for j=1:dim
                % Eq. (3.6)
                DeltaX(j,i)=(a*A(j,1)+c*C(j,1)+s*S(j,1)+f*F(j,1)+e*Enemy(j,1)) + w*DeltaX(j,i);
                if DeltaX(j,i)>Delta_max(j)
                    DeltaX(j,i)=Delta_max(j);
                end
                if DeltaX(j,i)<-Delta_max(j)
                    DeltaX(j,i)=-Delta_max(j);
                end
                X(j,i)=X(j,i)+DeltaX(j,i);
            end 
        end
        
        Flag4ub=X(:,i)>ub';
        Flag4lb=X(:,i)<lb';
        X(:,i)=(X(:,i).*(~(Flag4ub+Flag4lb)))+ub'.*Flag4ub+lb'.*Flag4lb;
        
    end
    Best_fitness=Food_fitness;
    Best_pos=Food_pos;
    
    Iter_curve(iter)=Best_fitness;
    History_pos{iter} = X;
    History_best{iter} = Best_pos;
end
end
%% 欧式距离
function o = distance(a,b)

for i=1:size(a,1)
    o(1,i)=sqrt((a(i)-b(i))^2);
end
end
%% 位置初始化
function Positions=initialization(SearchAgents_no,dim,ub,lb)

Boundary_no= size(ub,2); 

if Boundary_no==1
    ub_new=ones(1,dim)*ub;
    lb_new=ones(1,dim)*lb;
else
     ub_new=ub;
     lb_new=lb;   
end
for i=1:dim
    ub_i=ub_new(i);
    lb_i=lb_new(i);
    Positions(:,i)=rand(SearchAgents_no,1).*(ub_i-lb_i)+lb_i;
end

Positions=Positions';
end
%% Levy飞行
function o=Levy(d)

beta=3/2;
%Eq. (3.10)
sigma=(gamma(1+beta)*sin(pi*beta/2)/(gamma((1+beta)/2)*beta*2^((beta-1)/2)))^(1/beta);
u=randn(1,d)*sigma;
v=randn(1,d);
step=u./abs(v).^(1/beta);

% Eq. (3.9)
o=0.01*step;
end

4.参考文献

[1] Mirjalili S. Dragonfly algorithm: a new meta-heuristic optimization technique for solving single-objective, discrete, and multi-objective problems[J]. Neural computing and applications, 2016, 27: 1053-1073.
[2] Mantegna RN. Fast, accurate algorithm for numerical simulation of Lévy stable stochastic process. Phys Rev E 1994;49(5):4677–83.