算法介绍

        椭圆加密算法（ECC）是一种公钥加密体制，最初由Koblitz和Miller两人于1985年提出，其数学基础是利用椭圆曲线上的有理点构成Abel加法群上椭圆离散对数的计算困难性。公钥密码体制根据其所依据的难题一般分为三类：大素数分解问题类、离散对数问题类、椭圆曲线类。有时也把椭圆曲线类归为离散对数类。相比RSA，ECC优势是可以使用更短的密钥，来实现与RSA相当或更高的安全，RSA加密算法也是一种非对称加密算法，在公开密钥加密和电子商业中RSA被广泛使用。常用于通讯加密，数字签名等。据研究，160位ECC加密安全性相当于1024位RSA加密，210位ECC加密安全性相当于2048位RSA加密。bitcoin以及漂亮国gov都在用。相当好，但是由于后门问题等一些原因还未大量普及。

知识概念

        椭圆曲线

        公式如下图

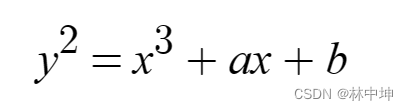
        a，b的取值满足

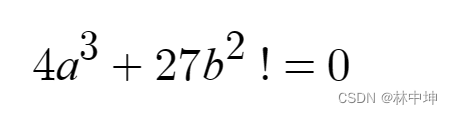
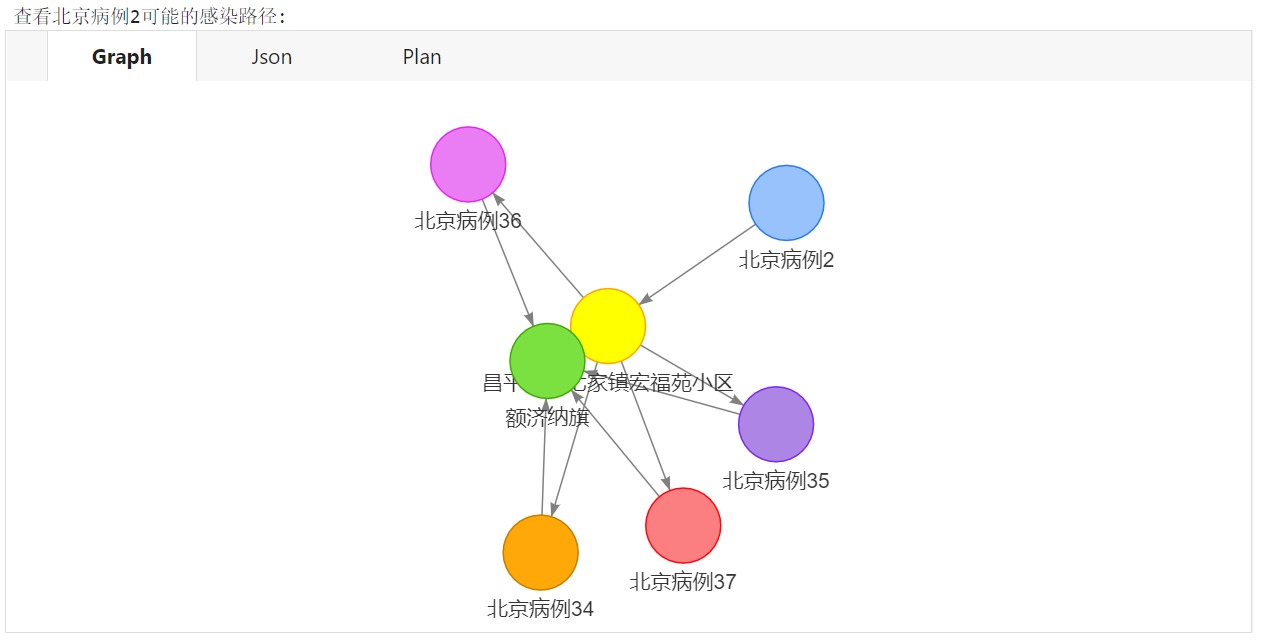
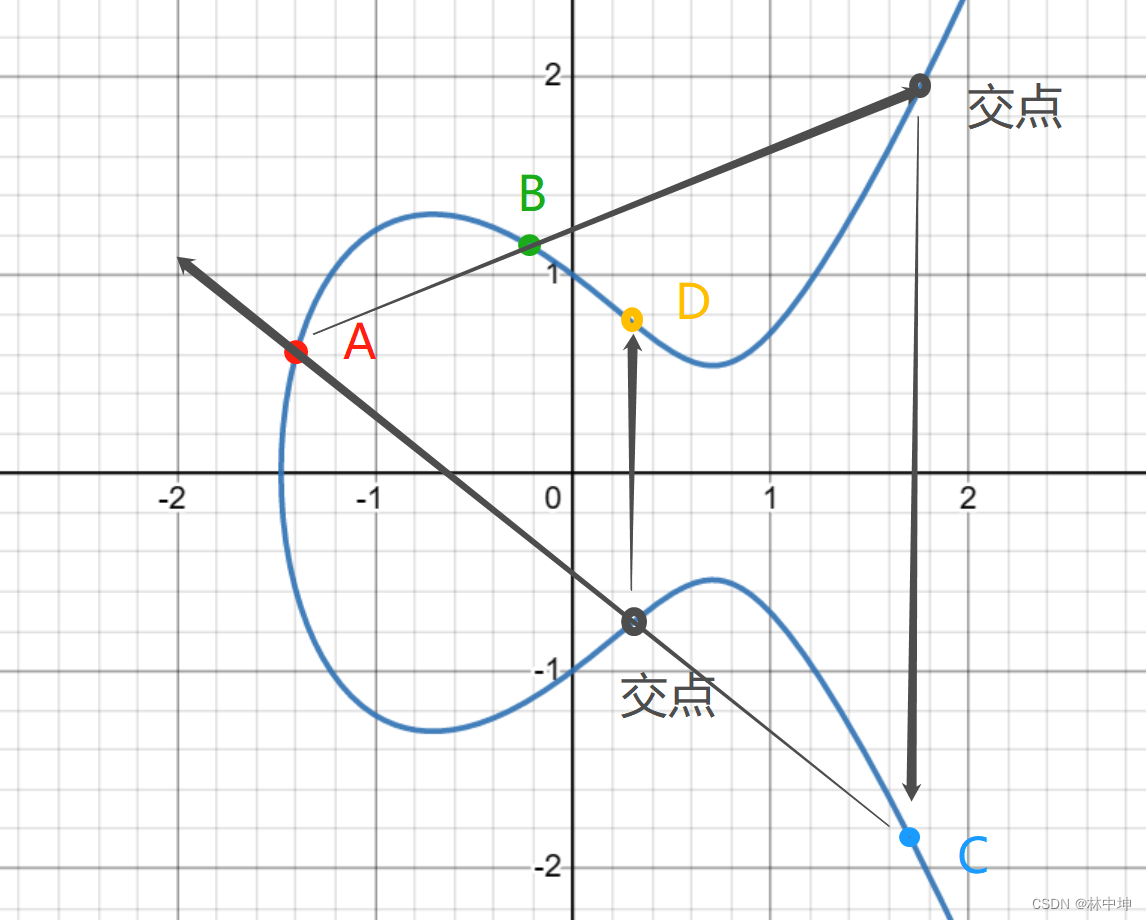
 下图为曲线的某一a，b值对应的坐标图

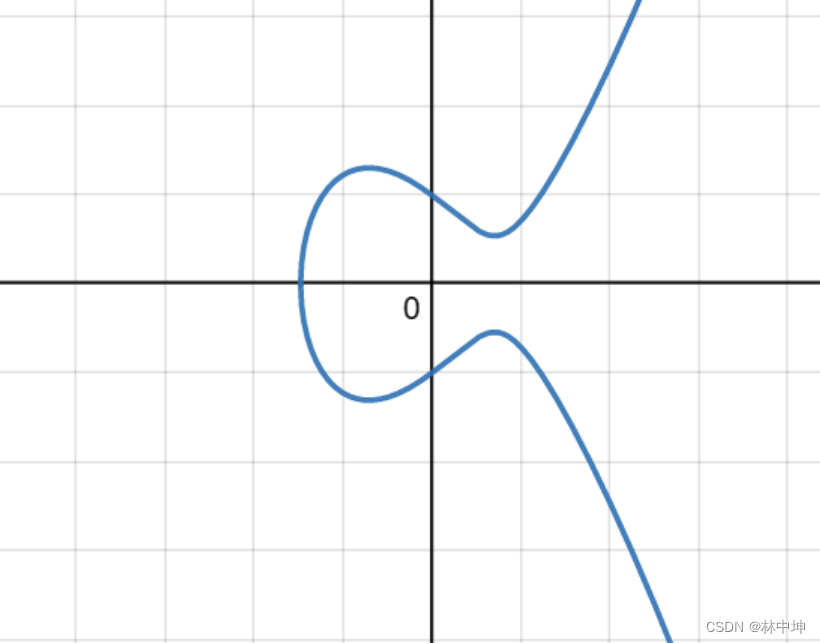
        当我们在曲线上随机取点A，B，其连线的延长线交于曲线上另外一点,交点点根据X轴的镜像对称，得到点C，点C再和A连线，又和曲线有个交点，此交点再镜像X轴得到点D，如此反复k次，得到最后一个点Q，该算法的难题就是，你知道起始点A,终点Q,但是你不知道中间经历了多少次运算，即正向算出Q点很简单，逆向算出k的值（也就是运算次数）很难。

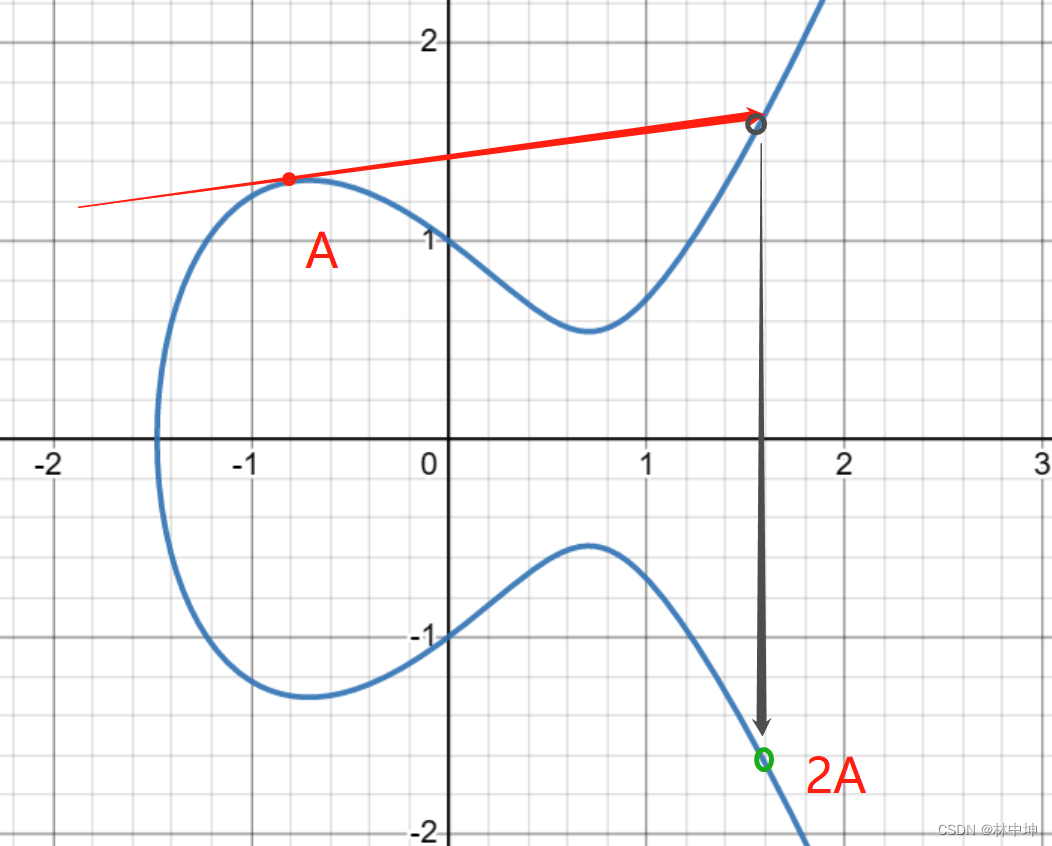
以上是A.B两个点，可以表示成A+B=C（这里不是简单的加运算，是数学运算，例如求斜率，求交点等）

那么如果AB两点无限接近，那么就等于一个A点做切线再镜像，可以表示成A+A=2A（这里不是简单的加运算，是数学运算，例如求斜率，求交点等）

点乘：Q=kP Q点就是最后的一个点，P点就是起点A.

 DH（Diffie-Hellman密钥协议算法）

           Diffie-Hellman密钥协议算法是一种确保共享密钥KEY安全穿越不安全网络的方法，它是OAKLEY的一个组成部分，由Whitefield与Martin Hellman在1976年提出。这个机制的巧妙在于需要安全通信的双方可以用这个方法确定对称密钥。然后可以用这个密钥进行加密和解密。但是注意，这个密钥交换协议/算法只能用于密钥的交换，而不能进行消息的加密和解密。双方确定要用的密钥后，要使用其他对称密钥操作加密算法实际加密和解密消息。

ECDH

椭圆曲线的特征加入DH算法的思想后，被称为ECDH，大致流程如下

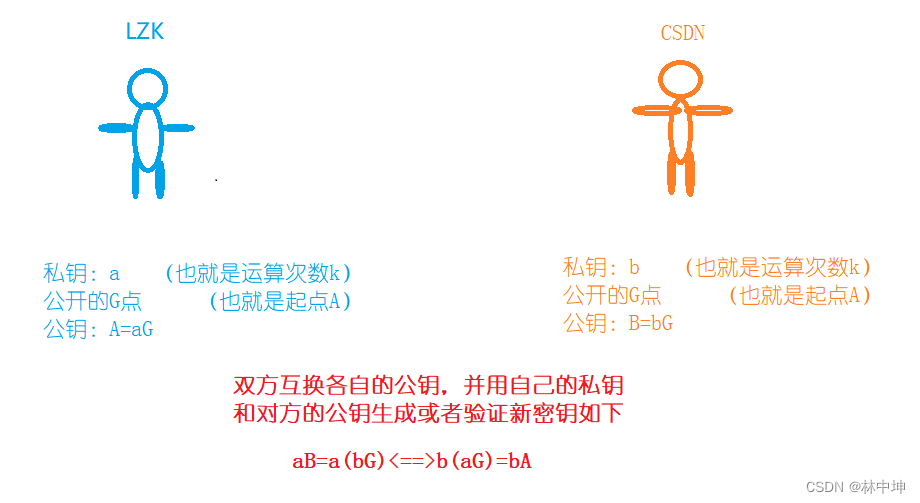
这就是ECDH的密钥交换算法。ECDHE的话是指临时性使用。

ECC加解密过程                                            

r：表示随机数

M：表示明文

Q：表示公钥（终点）

P：表示起始点

k：私钥

Q=kP ：即起点P经过k次运算得到Q点

2、选定⼀

解密: M+rQ-k(rP) = M+r(kP)-k(rP) = M

由于椭圆曲线是连续性的，不适用于密码学。所以要将其转化成 离散的有限域。

        在密码学中，有限域GF(p)是一个很重要的域，其中 p为素数（因为当p为素数时，才能保证集合中的所有的元素都有加法和乘法逆元(0除外) ）。简单来说，GF(p)就是 mod p， 因为一个数模p后，结果在[0, p -1]之间，即该域中有p个元素。对于元素a和b，那么(a+b) mod p和(a*b)mod p，其结果都是域中的元素。 GF(p)里面的加法和乘法都是平时用的加法和乘法。GF(p)的加法和乘法单位元分别是0和1，元素的加法和乘法逆元都很容易理解和求得，这里就不展开讲了，《密码编码学与网络安全》书中有详讲的。

 

        

        将椭圆曲线公式的取值做出限制，例如x,y的范围，x,y均为整数，运算结果向上上取整，设置p的值后，方程两边对p取模后，曲线将被限制在一个区域内,如下图，在取整后将成一个离散的有限域（绘图工具原因，看起来还有连续的，其实都是一个一个点了）。这个域里面的点的总数量n就叫做这个曲线的阶。

 最后，还有个问题，就是公钥Q(终点)是一个坐标点，怎么把它转换为序列值呢，就是将y值作为奇偶校验放在x值的前面就行了。由于主要了解原理，关于乘法逆元，阿贝尔群，以及椭圆曲线计算公式等知识这里不在说明，大家感兴趣的可以单独下来研究。

作图不易，转载请说明，学海无涯，若有错误，希望大家不吝赐教。