Before Writing
内容参考懒猫老师请多支持。
1 选择排序
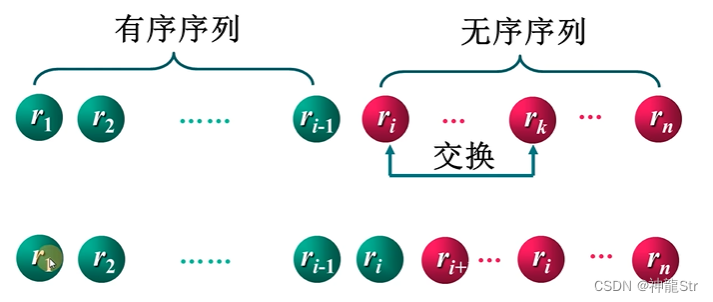
1-1 简单排序的原理
- 简单选择排序的主要思想是:每趟排序在当前待排序序列中选出关键码最小的记录,添加到有序序列中。
1-2 堆选择排序的原理
- 堆排序主要思想是:每次构造一个堆(二叉堆),将堆的根节点(最大值或最小值)添加到有序序列中。
- 将节点先按照大根堆或小根堆进行排序,这样在堆中的序列基本有序。后面再对该堆树进行调整就会加快效率。
1-2-1 堆的定义
- 堆是具有下列性质的完全二叉树:每个结点的值都小于或等于其左右孩子结点的值(称为小根堆),或每个节点的值大于左右孩子节点的值(称为大根堆)。
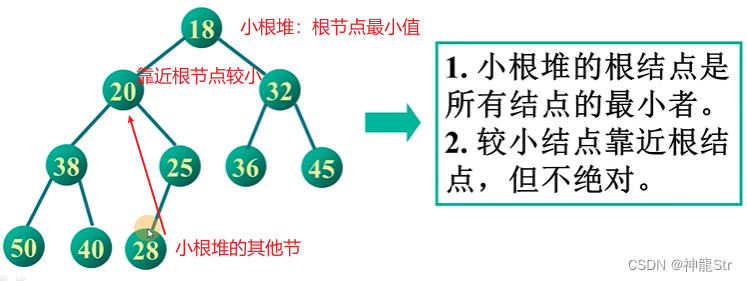
小根堆
- 小根堆的根节点是所有节点的最小值。
- 较小的节点靠近根节点但不绝对。
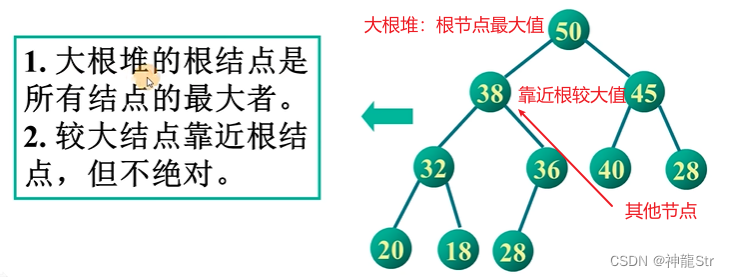
大根堆
- 根节点的值是所有节点的最大值。
- 较大节点靠近根节点,但不绝对。
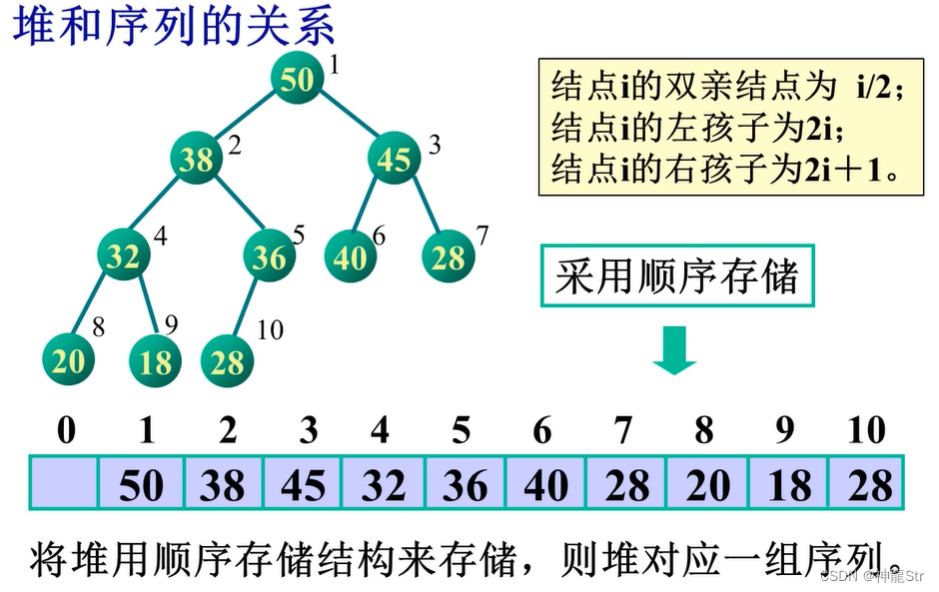
1-2-2 堆和序列的关系
- 将堆用顺序存储结构来存储,则堆对应一组序列。
- 比如对于完全二叉树:
- 节点序号为
i,左孩子序号为2i,右孩子2i+1,双亲节点i/2
- 节点序号为
1-2-3 基本思想
首先将待排序的记录序列构造成一个堆,此时,选出了堆中所有记录的最大者,然后将他从堆中移出,并将剩余的元素在调整称为堆,这样又找出了次大的记录,一次类推,直到堆中只有一个记录。
1-2-4 关键问题
- 如何由一个无需序列构建一个堆(初始堆)
- 如何处理对顶记录
- 如何调整剩余记录,成为一个新堆(重建堆)
堆调整
在一棵完全二叉树中,根节点的左右子树均是堆,如何调整根节点,使整个完全二叉树成为一个堆?
示例一:当一个树的左右子树都是大根堆堆,将其调整为大根堆
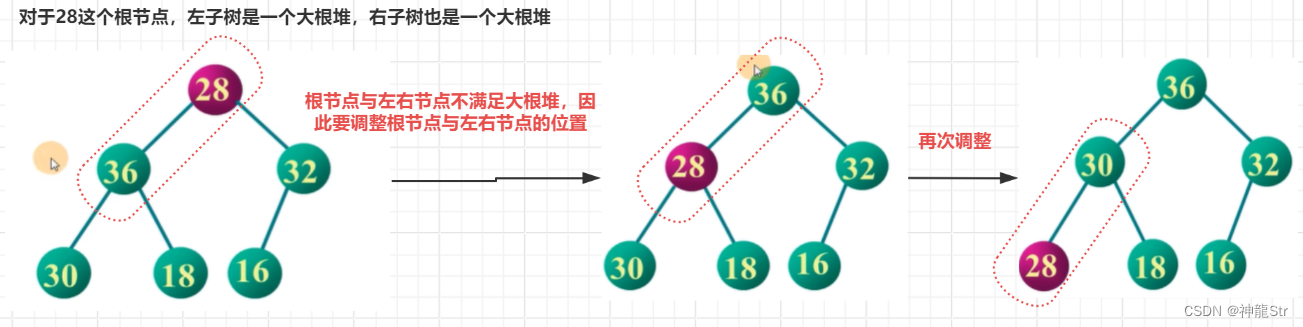
- 也就是说,首先要将根节点的左右子树都调整称为大根堆(从下往上处理子树),然后再调整根节点(从上往下处理根节点)。
- 可以见得堆排序流程就是根节点和左右孩子节点进行交换,其算法描述为:

关键问题1
- 如何将一个无需序列构建称为一个堆呢?
sift函数被调用一次就完成一个子树的构建,需要用一个循环反复调用这个函数,才能把无需序列构建称为一个堆。
算法描述:
// 从下往上进行处理,最后一个叶子结点的序号是n,n/2就是除去叶子节点的最后一个根节点
for (k = n/2; k >= 1; k --) {
sift(r, k, n);
}
最后一个节点(叶子)的序号是n,最后一个分支节点即为节点n的双亲,其序号是n/2。假如我们要调整一个堆,首先就调整左右子树进行处理,而最后一个叶子结点就是我们要处理的第一步。随后依次向上处理根节点也就是n/2 -> n/2 - 1 -> n/2 -2 -> ... ... -> 1直到最终的根节点,整体描述如下图:
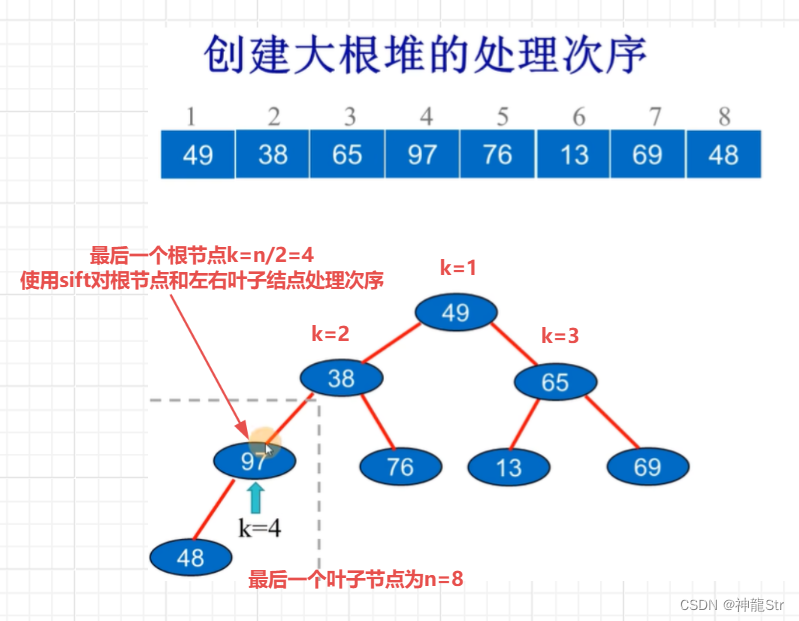
关键问题23
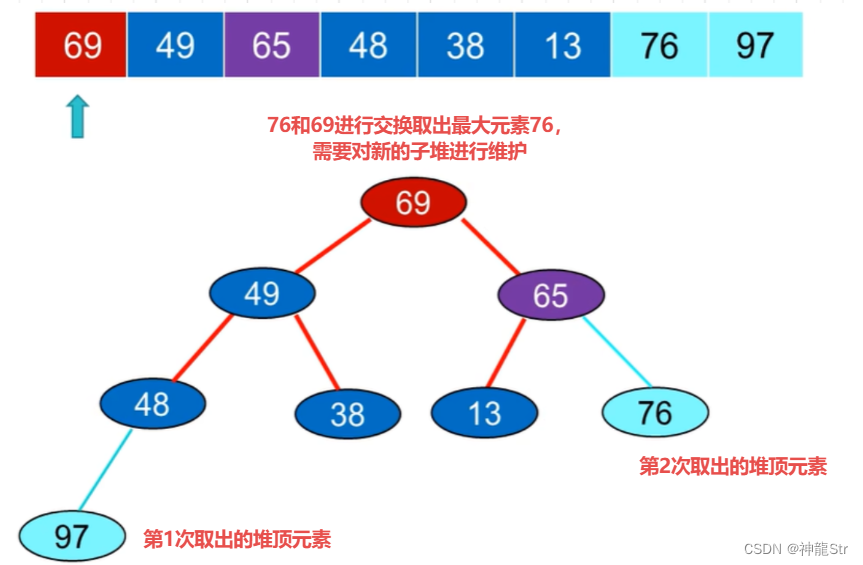
对堆顶进行记录:我们通过关键问题1对初始堆进行了构建,这个初始堆的特点是堆顶的元素是所有元素中最大的,接下来我们可以取出堆顶元素(最大元素)。然后重新对剩余的堆进行维护就能得到一个新的堆,将这个新的堆顶元素取出(次大元素)。
不断重复上面这个过程,就可以不断取得堆顶元素,最后获得排序后的序列。
算法描述:
- 第
k次处理堆顶是将堆顶记录r[1]与序列第n-k+1个记录r[n-k+1]交换。 r[1] <-> r[n-k+1]
// 元素个数为n,元素为r[]
void heapSort (int r[], int n) {
// 对堆进行初始构建
for (k = n/2; k >=1; k--) {
sift(r[], k, n);
}
// 依次取出堆顶元素,并动态维护剩余堆
for (k = 1; k < n; k++) {
// 获取堆顶元素,放在最后
switch(r[1], r[n-k+1]);
// 对剩余元素进行维护
sift(r[], 1, n-k);
}
}
1-2-5 算法分析
- 堆进行构建的时候遍历了每一个元素
for(int k = end/2; k >= 1; k--),因此算法时间复杂度为O(n)。只是进行元素交换,空间复杂度为O(1) - 对堆不断维护并构建的过程时,我们一共维护了
n次,每次都要进行近O(log(n))次比较。算法时间复杂度为O(n*log(n)),由于使用的是值交换而非递归,空间复杂度较低可以近似看做O(1)。