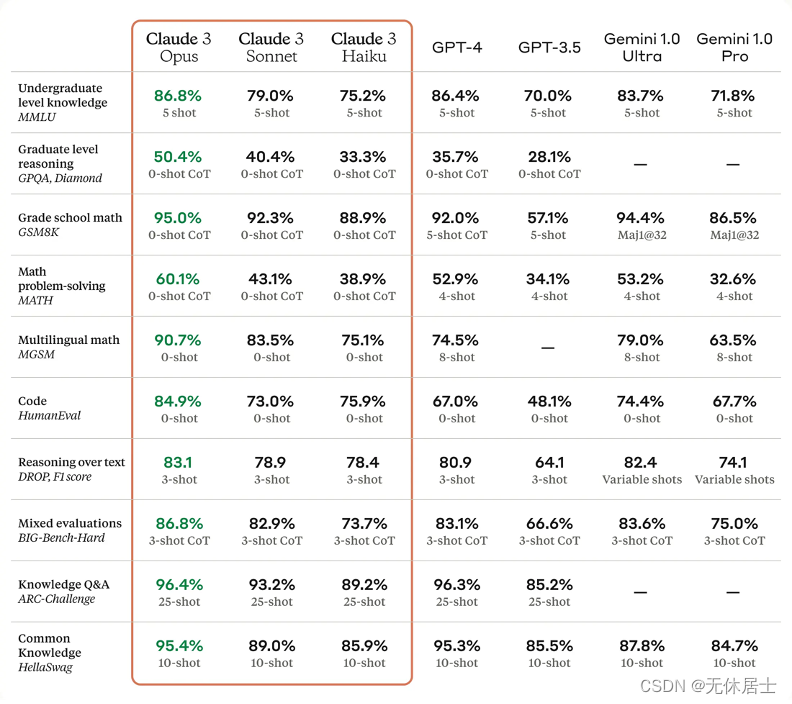
为什么学习KNN算法

KNN是监督学习分类算法，主要解决现实生活中分类问题。

（1）首先准备数据，可以是视频、音频、文本、图片等等

（2）抽取所需要的一些列特征，形成特征向量

（3）将这些特征向量连同标记一并送入机器学习算法中，训练出一个预测模型。

（4）采用同样的特征提取方法作用于新数据，得到用于测试的特征向量。

（5）使用预测模型对这些待测的特征向量进行预测并得到结果。

K近邻是机器学习算法中理论最简单，最好理解的算法，虽然算法简单，但效果也不错。

算法的思想：通过K个最近的已知分类的样本来判断未知样本的类别 

• 图像识别：KNN可以用于图像分类任务，例如人脸识别、车牌识别等。在图像识别领域，KNN通过计算测试图像与训练集中图像的相似度来进行分类。
• 文本分类：在文本分类方面，KNN算法可以应用于垃圾邮件过滤、情感分析等领域。通过对文本数据的特征提取和距离计算，KNN能够对新文本进行有效的分类。
• 回归预测：虽然KNN更常用于分类问题，但它也可以用于解决回归问题。在回归任务中，KNN通过找到最近的K个邻居，并根据它们的值来预测连续的输出变量。
• 医疗诊断：KNN算法可以辅助医生进行疾病的诊断。通过比较患者的临床数据与历史病例数据，KNN有助于识别疾病的模式和趋势。
• 金融风控：在金融领域，KNN可用于信用评分和欺诈检测。通过分析客户的交易行为和信用历史，KNN可以帮助金融机构评估风险。
• 推荐系统：KNN还可以用于构建推荐系统，通过分析用户的历史行为和其他用户的行为模式，为用户推荐商品或服务。

Sklearn API

鸢尾花Iris Dataset数据集是机器学习领域经典数据集，鸢尾花数据集包含了150条鸢尾花信息，每50条取自三个鸢尾花中之一：Versicolour、Setosa和Virginica。

from sklearn.datasets import load_iris
from sklearn.preprocessing import StandardScaler
from sklearn.neighbors import KNeighborsClassifier

if __name__ == '__main__':
      
    iris = load_iris() 

    # 数据标准化
    transformer = StandardScaler()
    x_ = transformer.fit_transform(iris.data) 

    # 模型训练
    estimator = KNeighborsClassifier(n_neighbors=3) # Knn中的K值
    estimator.fit(x_, iris.target) # 调用fit方法 传入特征和目标进行模型训练

    result = estimator.predict(x_) 
    print(result)

 数据集划分

 为了能够评估模型的泛化能力，可以通过实验测试对学习器的泛化能力进行评估，进而做出选择。因此需要使用一个测试集来测试学习器对新样本的判别能力。（2比8）

留出法：将数据集划分成两个互斥的集合：训练集，测试集。

交叉验证：将数据集划分为训练集，验证集，测试集 (验证集用于参数调整)。

留出法:

from sklearn.model_selection import train_test_split
from sklearn.model_selection import StratifiedShuffleSplit
from sklearn.model_selection import ShuffleSplit
from collections import Counter
from sklearn.datasets import load_iris


def test1():

    # 载数据集
    x, y = load_iris(return_X_y=True)
    print('原始类别比例:', Counter(y))

    # 留出法(随机分割)
    x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2)
    print('随机类别分割:', Counter(y_train), Counter(y_test))

    # 留出法(分层分割)
    x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2, stratify=y)
    print('分层类别分割:', Counter(y_train), Counter(y_test))


def test2():

    
    x, y = load_iris(return_X_y=True)
    print('原始类别比例:', Counter(y))
    print('*' * 40)

    # 多次划分(随机分割)
    spliter = ShuffleSplit(n_splits=5, test_size=0.2, random_state=0)
    for train, test in spliter.split(x, y):
        print('随机多次分割:', Counter(y[test]))

    print('*' * 40)

    # 多次划分(分层分割)
    spliter = StratifiedShuffleSplit(n_splits=5, test_size=0.2, random_state=0)
    for train, test in spliter.split(x, y):
        print('分层多次分割:', Counter(y[test]))


if __name__ == '__main__':
    test1()
    test2()

原始类别比例: Counter({0: 50, 1: 50, 2: 50})
随机类别分割: Counter({1: 41, 0: 40, 2: 39}) Counter({2: 11, 0: 10, 1: 9})
分层类别分割: Counter({2: 40, 0: 40, 1: 40}) Counter({2: 10, 1: 10, 0: 10})
原始类别比例: Counter({0: 50, 1: 50, 2: 50})
****************************************
随机多次分割: Counter({1: 13, 0: 11, 2: 6})
随机多次分割: Counter({1: 12, 2: 10, 0: 8})
随机多次分割: Counter({1: 11, 0: 10, 2: 9})
随机多次分割: Counter({2: 14, 1: 9, 0: 7})
随机多次分割: Counter({2: 13, 0: 12, 1: 5})
****************************************
分层多次分割: Counter({0: 10, 1: 10, 2: 10})
分层多次分割: Counter({2: 10, 0: 10, 1: 10})
分层多次分割: Counter({0: 10, 1: 10, 2: 10})
分层多次分割: Counter({1: 10, 2: 10, 0: 10})
分层多次分割: Counter({1: 10, 2: 10, 0: 10})

train_test_split 是一个函数，它用于将数据集划分为训练集和测试集。它可以随机地将数据集划分为两个子集，并可以指定划分的比例或数量。这个方法适用于大多数机器学习任务，特别是需要将数据集划分为训练集和测试集的情况。

而 ShuffleSplit 是一个类，它用于生成多个独立的训练/测试数据划分。与 train_test_split 不同，ShuffleSplit 会随机打乱数据集的顺序，然后根据指定的参数进行划分。这个方法适用于交叉验证的场景，特别是在需要多次划分数据集以评估模型性能的情况下。

总结来说，train_test_split 是一个简单的函数，用于将数据集划分为训练集和测试集；而 ShuffleSplit 是一个类，用于生成多个独立的训练/测试数据划分，适用于交叉验证的场景。

交叉验证法 

 

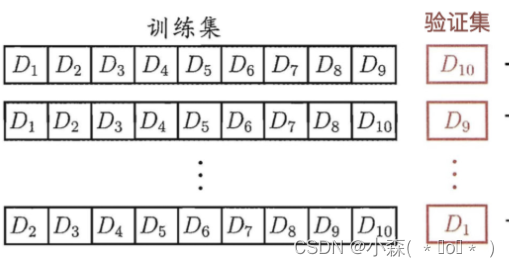
 K-Fold交叉验证，将数据随机且均匀地分成k分

• 第一次使用标号为0-8的共9份数据来做训练，而使用标号为9的这一份数据来进行测试，得到一个准确率
• 第二次使用标记为1-9的共9份数据进行训练，而使用标号为0的这份数据进行测试，得到第二个准确率
• 以此类推，每次使用9份数据作为训练，而使用剩下的一份数据进行测试，共进行10次训练，最后模型的准确率为10次准确率的平均值

from sklearn.model_selection import KFold
from sklearn.model_selection import StratifiedKFold
from collections import Counter
from sklearn.datasets import load_iris

def test():

    
    x, y = load_iris(return_X_y=True)
    print('原始类别比例:', Counter(y))
    print('*' * 40)

    #  随机交叉验证
    spliter = KFold(n_splits=5, shuffle=True, random_state=0)
    for train, test in spliter.split(x, y):
        print('随机交叉验证:', Counter(y[test]))

    print('*' * 40)

    # 分层交叉验证
    spliter = StratifiedKFold(n_splits=5, shuffle=True, random_state=0)
    for train, test in spliter.split(x, y):
        print('分层交叉验证:', Counter(y[test]))

 随机交叉验证: Counter({1: 13, 0: 11, 2: 6})
随机交叉验证: Counter({2: 15, 1: 10, 0: 5})
随机交叉验证: Counter({0: 10, 1: 10, 2: 10})
随机交叉验证: Counter({0: 14, 2: 10, 1: 6})
随机交叉验证: Counter({1: 11, 0: 10, 2: 9})
****************************************
分层交叉验证: Counter({0: 10, 1: 10, 2: 10})
分层交叉验证: Counter({0: 10, 1: 10, 2: 10})
分层交叉验证: Counter({0: 10, 1: 10, 2: 10})
分层交叉验证: Counter({0: 10, 1: 10, 2: 10})
分层交叉验证: Counter({0: 10, 1: 10, 2: 10})

分类算法的评估 

• 利用训练好的模型使用测试集的特征值进行预测

• 将预测结果和测试集的目标值比较，计算预测正确的百分比

from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier
#加载鸢尾花数据集
X,y = datasets.load_iris(return_X_y = True)
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.2)

knn_clf = KNeighborsClassifier(n_neighbors=6)

knn_clf.fit(X_train,y_train)
y_predict = knn_clf.predict(X_test)
sum(y_predict==y_test)/y_test.shape[0]
# 0.8666666666666667

 SKlearn中模型评估

• sklearn.metrics包中的accuracy_score方法: 传入预测结果和测试集的标签， 返回预测准确率

from sklearn.metrics import accuracy_score
accuracy_score(y_test,y_predict)

如何确定合适的K值

K值过小：容易受到异常点的影响

k值过大：受到样本均衡的问题

我们可以采用交叉验证法来选择最优的K值。

GridSearchCV

GridSearchCV 是 scikit-learn 库中的一个类，用于进行参数网格搜索。它结合了交叉验证和网格搜索的功能，可以自动地对给定的模型和参数组合进行训练和评估，以找到最佳的参数设置。

from sklearn.model_selection import GridSearchCV
from sklearn.svm import SVC

# 定义模型和参数网格
model = SVC()
param_grid = {'C': [0.1, 1, 10], 'kernel': ['linear', 'rbf']}

# 创建 GridSearchCV 对象并进行训练
grid_search = GridSearchCV(estimator=model, param_grid=param_grid, cv=5)
grid_search.fit(X_train, y_train)

# 获取最佳参数和对应的评分
best_params = grid_search.best_params_
best_score = grid_search.best_score_

# 使用最佳参数重新训练模型
best_model = grid_search.best_estimator_
best_model.fit(X_train, y_train)

# 在测试集上进行预测
y_pred = best_model.predict(X_test)

GridSearchCV 会遍历所有可能的参数组合，并对每个组合进行交叉验证。这可能会消耗大量的计算资源和时间，特别是当参数空间较大时。因此，在使用 GridSearchCV 时，需要权衡参数网格的大小和计算资源的可用性。

from sklearn.model_selection import GridSearchCV
x, y = load_iris(return_X_y=True)

x_train, x_test, y_train, y_test = \
    train_test_split(x, y, test_size=0.2, stratify=y, random_state=0)

# 创建网格搜索对象
estimator = KNeighborsClassifier()
param_grid = {'n_neighbors': [1, 3, 5, 7]}
estimator = GridSearchCV(estimator, param_grid=param_grid, cv=5, verbose=0)
estimator.fit(x_train, y_train)

print('最优参数组合:', estimator.best_params_, '最好得分:', estimator.best_score_)

print('测试集准确率:', estimator.score(x_test, y_test))

# 最优参数组合: {'n_neighbors': 7} 最好得分: 0.9583333333333334
# 测试集准确率: 1.0

手写数字案例

数据集：可以从MNIST数据集或UCI欧文大学机器学习存储库中获取手写数字的数据。这些数据集包含了大量已经标注好的手写数字图片。

import matplotlib.pyplot as plt
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier
import joblib
from collections import Counter

def show_digit(idx):
    
    data = pd.read_csv('手写数字识别.csv')
    if idx < 0 or idx > len(data) - 1:
        return
    x = data.iloc[:, 1:]
    y = data.iloc[:,0]
    print('当前数字的标签为:',y[idx])    # 查看当前数字的数值

    
    data_ = x.iloc[idx].values
    # 将数据形状修改为 28*28
    data_ = data_.reshape(28, 28)     # 显示当前数字在数据集的图片
    
    # 显示图像
    plt.imshow(data_)
    plt.show()

def train_model():

    # 1. 加载手写数字数据集
    data = pd.read_csv('手写数字识别.csv')
    x = data.iloc[:, 1:] / 255
    y = data.iloc[:, 0]

    # 2. 打印数据基本信息
    print('数据基本信息:', x.shape)
    print('类别数据比例:', Counter(y))

    # 3. 分割数据集
    split_data = train_test_split(x, y, test_size=0.2, stratify=y, random_state=0)
    x_train, x_test, y_train, y_test = split_data

    # 4. 模型训练
    estimator = KNeighborsClassifier(n_neighbors=3)
    estimator.fit(x_train, y_train)

    # 5. 模型评估
    acc = estimator.score(x_test, y_test)
    print('测试集准确率: %.2f' % acc)

    # 6. 模型保存
    joblib.dump(estimator, 'knn.pth')


def test_model():
    # 读取图片数据
    import matplotlib.pyplot as plt
    import joblib
    img = plt.imread('demo.png') # 对于灰度图像，返回的是一个二维数组，其中每个元素是一个介于0和1之间的浮点数，表示该像素的灰度值
    plt.imshow(img)
    # 加载模型
    knn = joblib.load('knn.pth')
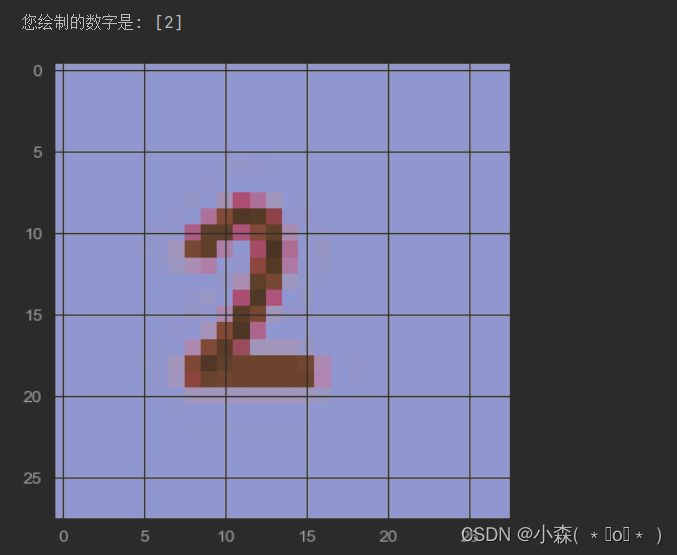
    y_pred = knn.predict(img.reshape(1, -1)) #首先将从图片中读取到的数据 (img) 重塑为一维数组形式，以便给 KNN 分类器进行预测。
    print('您绘制的数字是:', y_pred)


show_digit(1)
    # 训练模型
train_model()
    # 测试模型
test_model()

 

 

小结： 

---

KNN（K-Nearest Neighbors）算法，即K最近邻算法，是一种监督学习算法，可以用于分类和回归问题。其基本思想是：给定一个训练数据集，对于新的输入实例，在训练数据集中找到与该实例最邻近的K个实例，这K个实例的多数属于某个类别，则该输入实例也属于这个类别。

KNN算法的主要步骤如下：

1. 计算输入实例与训练数据集中的每个实例之间的距离。常用的距离度量方法有欧氏距离、曼哈顿距离等。

2. 对计算出的距离进行排序，找出距离最近的K个邻居。

3. 统计这K个邻居所属的类别，选择出现次数最多的类别作为输入实例的预测类别。

4. 如果用于回归问题，则计算这K个邻居的平均值或加权平均值作为输入实例的预测值。

KNN算法的优点：

1. 算法简单，易于理解。

2. 适用于多分类问题。

3. 对于一些非线性问题，KNN算法具有较好的性能。

KNN算法的缺点：

1. 当训练数据集较大时，计算距离的时间复杂度较高。

2. K值的选择对算法性能影响较大，但目前没有确定K值的通用方法。

3. 对于不平衡数据集，KNN算法的性能较差。