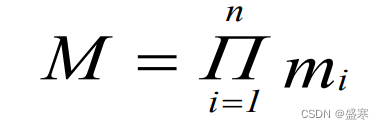个人专栏—塑性力学

1.1 塑性力学基本概念 塑性力学基本概念
1.2 弹塑性材料的三杆桁架分析 弹塑性材料的三杆桁架分析
1.3 加载路径对桁架的影响 加载路径对桁架的影响

---

---

$应力$：内力的分布集度

• 全应力

$$p=\underset{\Delta A\to 0}{\lim }\frac{\Delta P}{\Delta A}=\frac{\mathrm{d}\mathbf{P}}{\mathrm{d}A}$$

• 正应力:垂直于截面的应力

$$\sigma =\underset{\Delta A\to 0}{\lim }\frac{\Delta N}{\Delta A}=\frac{\mathrm{d}\mathbf{N}}{\mathrm{d}A}$$

• 剪应力: 位于截面上的应力

$$\epsilon =\underset{\Delta A\to 0}{\lim }\frac{\Delta T}{\Delta A}=\frac{\mathrm{d}\mathbf{T}}{\mathrm{d}A}$$

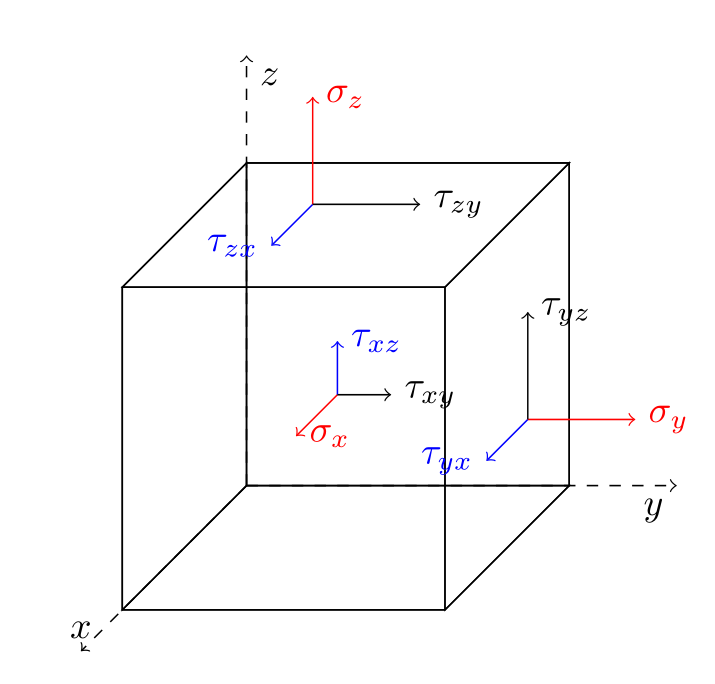
$单元体$： 构件内点的代表物，是包围被研究点的无限小几何体，常用正六面体表示。

• 正应力 $\sigma_i $表示作用在垂直 $i $轴的面上，方向沿 $i $轴的应力；

• 剪应力 $\tau_{ij} $表示作用在垂直 $i $轴的面上，方向沿 $j $轴的应力；

• 剪应力互等定理

$${\tau }_{xy}={\tau }_{yx}{\tau }_{yz}=\tau -zy{\tau }_{xz}={\tau }_{zx}$$

$应力张量$：应力张量是描述物体内部应力状态的物理量，它是一个二阶张量。二阶表示它有两个指标，而张量表示它在坐标系变换下的变换规律。

• 应力张量的元素可以表示为${\sigma }_{ij}$，其中$i$和$j$分别表示坐标轴的索引。这些元素表示了在某个点上，物体内部在不同方向上的应力大小和方向。例如，${\sigma }_{xx}$表示物体在x轴上的正向应力分量，${\sigma }_{xy}$表示物体在x轴和y轴之间的剪切应力分量。

• 应力张量为二阶对称张量: $\sigma_{ij}=\sigma_{ji} $，任一点的应力状态完全由应力张量确定；

$${\sigma }_{ij}=\left[\begin{array}{ccc}{\sigma }_x& {\tau }_{xy}& {\tau }_{xz}\\ {\tau }_{yx}& {\sigma }_y& {\tau }_{yz}\\ {\tau }_{zx}& {\tau }_{zy}& {\sigma }_z\end{array}\right]=\left[\begin{array}{ccc}{\sigma }_{11}& {\sigma }_{12}& {\sigma }_{13}\\ {\sigma }_{21}& {\sigma }_{22}& {\sigma }_{23}\\ {\sigma }_{31}& {\sigma }_{32}& {\sigma }_{33}\end{array}\right]$$

• 应力张量的对称性是由物体力学平衡和牛顿第三定律所决定的。根据力学平衡的要求，物体内部的力矩必须为零，而对称性是力矩为零的一个必要条件。另外，根据牛顿第三定律，作用于物体上的力和反作用力必须相等且方向相反。这意味着应力张量在不同坐标轴上的应力分量必须满足对称性。

在外力作用下，物体的变形可分为体积变形和形状变形，由静水压力试验结果可知，静水压力只引起体积变化，而不改变形状改变，故可将应力张量进行分解：

$$\begin{array}{rl}{\sigma }_m& =\frac{{\sigma }_x+{\sigma }_y+{\sigma }_z}{3}=\frac{{\sigma }_1+{\sigma }_2+{\sigma }_3}{3}\\ {\sigma }_{ij}& =\left[\begin{array}{ccc}{\sigma }_x& {\tau }_{xy}& {\tau }_{xz}\\ {\tau }_{yx}& {\sigma }_y& {\tau }_{yz}\\ {\tau }_{zx}& {\tau }_{zy}& {\sigma }_z\end{array}\right]\\ & =\left[\begin{array}{ccc}{\sigma }_m& 0& 0\\ 0& {\sigma }_m& 0\\ 0& 0& {\sigma }_m\end{array}\right]+\left[\begin{array}{ccc}{\sigma }_x-{\sigma }_m& {\tau }_{xy}& {\tau }_{xz}\\ {\tau }_{yx}& {\sigma }_y-{\sigma }_m& {\tau }_{yz}\\ {\tau }_{zx}& {\tau }_{zy}& {\sigma }_z-{\sigma }_m\end{array}\right]\\ & ={\sigma }_m{\delta }_{ij}+S_{ij}\\ {\delta }_{ij}& =\{\begin{array}{ll}1& i=j\\ 0& i\ne j\end{array}=\left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right]\to {\sigma }_m{\delta }_{ij}=\left[\begin{array}{ccc}{\sigma }_m& 0& 0\\ 0& {\sigma }_m& 0\\ 0& 0& {\sigma }_m\end{array}\right]\end{array}$$

• 应力球张量（静水压力）

  1. 任意截面上的均值应力等于 $\sigma_m $;

  2. 应力球张量与坐标的选择无关；

  3. 应力球张量与材料体积变形有关；

• 应力偏张量$S_{ij} $

  1. 应力偏张量材料形变有关，即与塑性变形有关；

  2. 应力偏张量为对称张量。

应用示例

已知某点的应力状态 KaTeX parse error: {equation*} can be used only in display mode.，将该应力状态写成张量形式并分解。

$$\begin{array}{c}{\sigma }_{ij}=\left[\begin{array}{ccc}{\sigma }_x& {\tau }_{xy}& {\tau }_{xz}\\ {\tau }_{yx}& {\sigma }_y& {\tau }_{yz}\\ {\tau }_{zx}& {\tau }_{zy}& {\sigma }_z\end{array}\right]=\left[\begin{array}{ccc}1000& 150& 0\\ 150& 500& 70\\ 0& 70& 0\end{array}\right]\\ {\sigma }_m=\frac{{\sigma }_x+{\sigma }_y+{\sigma }_z}{3}=500\end{array}$$

$$\begin{array}{rl}{\sigma }_{ij}& =\left[\begin{array}{ccc}{\sigma }_m& 0& 0\\ 0& {\sigma }_m& 0\\ 0& 0& {\sigma }_m\end{array}\right]+\left[\begin{array}{ccc}{\sigma }_x-{\sigma }_m& {\tau }_{xy}& {\tau }_{xz}\\ {\tau }_{yx}& {\sigma }_y-{\sigma }_m& {\tau }_{yz}\\ {\tau }_{zx}& {\tau }_{zy}& {\sigma }_z-{\sigma }_m\end{array}\right]\\ & =\left[\begin{array}{ccc}500& 0& 0\\ 0& 500& 0\\ 0& 0& 500\end{array}\right]+\left[\begin{array}{ccc}500& 150& 0\\ 150& 0& 70\\ 0& 70& -500\end{array}\right]\end{array}$$

---

承接DIC数据图像处理模拟散斑制作（斑点直径≥0.1mm）及DIC散斑图像代处理：

如果你喜欢以上内容，或者对塑性力学感兴趣，欢迎一键三连，博主将持续更新，如果有任何问题，可以咨询博主，非常乐意为大家解答。