MATLAB基本操作
1. 对象定义 使用sym定义单个对象、使用syms定义多个对象
2. 使用limit求极限
$$ \lim_{v \rightarrow a} f(x) $$
limit(f,v,a) % 使用limit(f,v,a,'left')可求左极限3. 导数 使用diff(f,v,n)对$ f(v)=v^{t-1} $求 $ n $ 阶导 $ \frac{d^nf}{d^nv} $,n缺省时,默认为1,diff(f)默认求一阶导数。
4. 定积分和不定积分 使用int(f,v)求f对变量v的不定积分,使用int(f,v,a,b)求f对变量v的定积分,a、b为积分上下标。$ \int{f(v)dv} $、$ \int^{a}_{b}{f(v)dv} $。
5. matlab函数文件定义形式
function [输出形参列表] = 函数名(输入形参列表)
函数体function spir_len = spirallength(d, n, lcolor)
% SPIRALLENGTH plot a circle of radius as r in the provided color and calculate its area
% 输入参数:
% d: 螺旋的旋距
% n: 螺旋的圈数
% lcolor:画图线的颜色
% 输出参数:
% spir_len:螺旋的周长
% 调用说明:
% spirallength(d,n):以参数d,n画螺旋线,螺旋线默认为蓝色
% spirallength(d,n,lcolor):以参数d,n,lcolor画螺旋线
% spir_len = spirallength(d,n):计算螺旋线的周长,并以蓝色填充螺旋线
% spir_len = spirallength(d,n,lcolor):计算螺旋线的周长,并以lcolor颜色填充螺旋线
% 版本号V1.0,编写于1999年9月9号,修改于1999年9月10号,作者:亚索
if nargin > 3
error('输入变量过多!');
elseif nargin == 2
lcolor = 'b'; % 默认情况下为蓝色
end
j = sqrt(-1);
phi = 0 : pi/1000 : n*2*pi;
amp = 0 : d/2000 : n*d;
spir = amp .* exp(j*phi);
if nargout == 1
spir_len = sum(abs(diff(spir)));
fill(real(spir), imag(spir), lcolor);
elseif nargout == 0
plot(spir, lcolor);
else
error('输出变量过多!');
end
axis('square');6. matlab程序设计语句
% for循环
for 循环变量=初值:步长:终值
循环体
end
% while循环
while 条件
循环体
end
% if语句
if 条件
语句组1
elseif
语句组2
else
语句组3
end
% switch语句
switch 表达式
case 表达式1
语句组1
case 表达式2
语句组2
... ...
case 表达式m
语句组m
otherwise
语句组
end
% try语句
try
语句组1 %语句组1若正确则跳出该结构
catch
语句组2
end7. 矩阵操作
| 操作 | 作用 |
|---|---|
| size(A) | 求矩阵A的行数和列数 |
| length(x) | 返回向量x的长度 |
| A' | A的转置 |
| A(:,n) | 取矩阵A第n列数,A(n,:)取第n行 |
| det(A) | 求矩阵A的行列式 |
| inv(A) | 求A的逆 |
| rank(A) | 求A的秩 |
| trace(A) | 求A的迹 |
| max(A)、min(A) | 求A的各列最大、最小元素 |
| mean(A) | 求A各列的平均值 |
| sum(A) | 求A各列元素之和 |
8. matlab简单绘图
plot函数是MATLAB中最核心的二维绘图函数,有诸多语法格式,可实现多种功能。常用格式有:
- plot(x):缺省自变量的绘图格式,x可为向量或矩阵。
- plot(x, y):基本格式,x和y可为向量或矩阵。
- plot(x1, y1, x2, y2,…):多条曲线绘图格式,在同一坐标系中绘制多个图形。
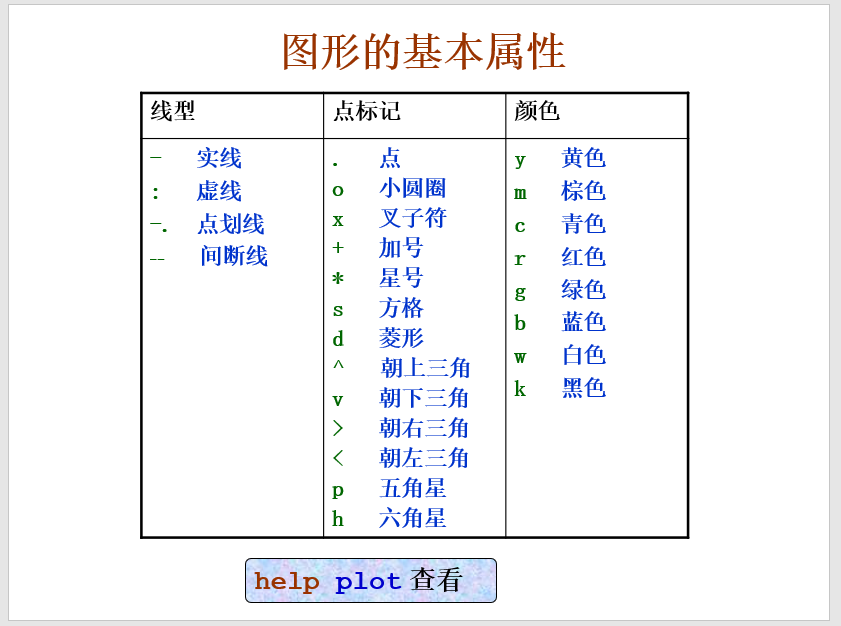
- plot(x, y,‘s’):开关格式,开关量字符串s设定了图形曲线的颜色、线型及标示符号(见下表)。
无约束优化问题求解
fminbnd、fminunc函数输出变量解释
| 变量 | 描述 |
|---|---|
| x | 由优化函数求得的值. 若exitflag>0,则x为解; 否则,x不是最终解, 它只是迭代制止时优化过程的值 |
| fval | 解 x 处的目标函数值 |
| exitflag | 描述退出条件:exitflag>0,表目标函数收敛于解x处;exitflag=0,表已达到函数评价或迭代的最大次数;exitflag<0,表目标函数不收敛 |
| output | 包含优化结果信息的输出结构。Iterations:迭代次数;Algorithm:所采用的算法;FuncCount:函数评价次数 |
一元函数无约束优化问题-fminbnd
常用格式
$$ min f(x), x_1<x<x_2 $$
(1)x= fminbnd (fun, x1, x2) (2)x= fminbnd (fun, x1, x2 , options) (3)[x , fval]= fminbnd(...) (4)[x , fval , exitflag]= fminbnd(...) (5)[x , fval , exitflag , output]= fminbnd(...) 函数fminbnd的算法基于黄金分割法和二次插值法,它要求目标函数必须是连续函数,并可能只给出局部最优解
例子
求函数 $ f(x)=2e^{-x}sin(x) $ 在 $ 0<x<8 $ 时的最小值
% 如果求最大需要对f取反
f = @(x) (2*exp(-x)*sin(x));
[x,fval] = fminbnd(f,0,8);
x
fval多元函数无约束优化问题-fminunc
常用格式
$$ min f(X),这里X为n维变量 $$ fminunc常用格式为: (1)x= fminunc(fun, X0); (2)x= fminunc(fun, X0,options); (3)[x,fval]= fminunc(...); (4)[x,fval,exitflag]= fminunc(...); (5)[x,fval,exitflag,output]= fminunc(...) 其中 X0为初始值
例子
求函数$ f(x_1,x_2)=(4x_1^2+2x_2^2+4x_1x_2+2x_2^2+1)e^x $的最小值,$ X_0=[-1,1] $
f = @(x) (4*x(1)^2+2*x(2)^2+4*x(1)*x(2)+2*x(2)+1)*exp(x(1));
x0 = [-1,1];
[x,fval] = fminunc(f, x0);
x
fval线性规划问题求解
使用linprog求解一般线性规划问题
常见问题(linprog默认求最小值) $$ minz=cX $$
$$ s.t. \begin{cases} AX\leq{b}\ Aeq\cdot{X}=beq\ VLB\leq{X}\leq{VUB} \end{cases}$$
求解命令
[x,fval] = linprog(c,A,b,Aeq,beq,VLB,VUB)例子
$$ min z=13x_1+9x_2+10x_3+11x_4+12x_5+8x_6 $$
$$ s.t.\left{ \begin{aligned} & x_1+x_2=400\ & x_2+x_5=600\ & x_3+x_6=500\ & 0.4x_1+1.1x_2+x_3\leq{800}\ & 0.5x_4+1.2x_5+1.3x_6\leq{900}\ & x_i\geq0,i=1,2,...,6 \end{aligned} \right. $$
f = [13 9 10 11 12 8];
A = [0.4 1.1 1 0 0 0
0 0 0 0.5 1.2 1.3];
b = [800; 900];
Aeq=[1 0 0 1 0 0
0 1 0 0 1 0
0 0 1 0 0 1];
beq=[400 600 500];
vlb = zeros(6,1);
vub=[];
[x,fval] = linprog(f,A,b,Aeq,beq,vlb,vub)使用bintprog求解0-1规划问题
matlab2014以上版本使用intlinprog求解0-1规划问题
$$ minz=cX $$
$$ s.t. \begin{cases} AX\leq{b}\ Aeq\cdot{X}=beq\ X为0-1变量 \end{cases}$$
% 命令
[x,fval] = bintprog(c,A,b,Aeq,beq)例子
$$ min z=3x_1+7x_2-x_3+x_4 $$ $$ s.t. \begin{cases} 2x_1-x_2+x_3-x_4\geq{1}\ x_1-x_2+6x_3+4x_4\geq{8}\ 5x_1+3x_2+x_4\geq{5}\ x_i=0或1(i=1,2,3,4) \end{cases} $$
z = [3;7;-1;1];
A = [-2 1 -1 1;
-1 1 -6 -4;
-5 -3 0 -1];
b = [-1;-8;-5];
Aeq = [];
beq = [];
[x,fval] = bintprog(z,A,b,Aeq,beq)数据插值与拟合
数据插值,使用interpl进行一维插值
matlab命令
yi = interpl(X,Y,xi,method)该命令用指定的算法找出一个一元函数,然后以该函数给出xi处的值。其中x=[x1,x2,…,xn]’和 y=[y1,y2,…,yn]’两个向量分别为给定的一组自变量和函数值,用来表示已知样本点数据;xi为待求插值点处横坐标,可以是一个标量,也可以是一个向量,是向量时,必须单调;yi得到返回的对应纵坐标。
- method可以选取以下方法之一:
- ‘nearest’:最近邻点插值,直接完成计算;
- ‘spline’:三次样条函数插值;
- ‘linear’:线性插值(缺省方式),直接完成计算;
- ‘cubic’:三次函数插值;
例子
作函数$ y=(x^2-3x+7)e^{-4x}sin(2x) $在[0,1]取间隔为0.1的点图,用插值进行实验
x=0:0.1:1;
y=(x.^2-3*x+7).*exp(-4*x).*sin(2*x); %产生原始数据
subplot(1,2,1);
plot(x,y,x,y,'ro') %作图
xx=0:0.02:1; %待求插值点
yy=interp1(x,y,xx,'spline'); %此处可用nearest,cubic,spline分别试验
subplot(1,2,2)
plot(x,y,'ro',xx,yy,'b') %作图曲线拟合
拟合函数polyfit
p=polyfit(x,y,n)
[p,s]= polyfit(x,y,n)说明:x,y为数据点,n为多项式阶数,返回p为幂次从高到低的多项式系数向量p。p是n+1维参数向量p(1),p(2)….那么拟合后对应的多项式即为: $$ p(1)x^n+p(2)x^{n-1}+\cdot\cdot\cdot+p(n)x+p(n+1) $$
x必须是单调的。矩阵s用于生成预测值的误差估计
多项式求值函数polyval
y=polyval(p,x)
[y,DELTA]=polyval(p,x,s)说明:y=polyval(p,x)为返回对应自变量x在给定系数p的多项式的值; [y,DELTA]=polyval(p,x,s) 使用polyfit函数的选项输出s得出误差估计DELTA。它假设polyfit函数数据输入的误差是独立正态的,并且方差为常数。则DELTA将至少包含50%的预测值。
例子
求如下给定数据的拟合曲线 x=[0.5,1.0,1.5,2.0,2.5,3.0],y=[1.75,2.45,3.81,4.80,7.00,8.60]
x=[0.5,1.0,1.5,2.0,2.5,3.0];
y=[1.75,2.45,3.81,4.80,7.00,8.60];
plot(x,y,‘*r’) %先观察数据点的大致形态
p=polyfit(x,y,2) %用二次多项式拟合
x1=0.5:0.05:3.0; % 步长0.05
y1=polyval(p,x1);
plot(x,y,'*r',x1,y1,'-b')本文由博客群发一文多发等运营工具平台 OpenWrite 发布