微❤关注“电气仔推送”获得资料(专享优惠)
简介
四桥臂三相逆变器 电路 的一般形式如图 1,为 便于分析 ,将其等效成图所示的电路 。以直流母线电压Ud的 1/2处为参考点 ,逆变器三相和零线相 输 出可等效成 2个压控电压源 。
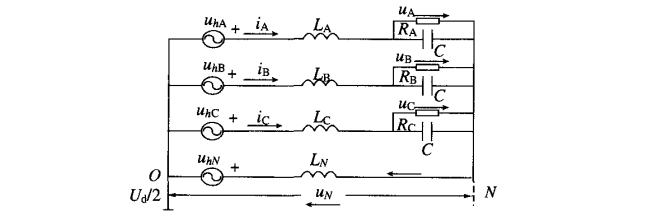
将三相滤波电感和零线相滤波电感看作是 电源的内 部阻抗,通过引入变量及变换控制的方式,经等效 变换,将零线相阻抗值变换为零,同时,将其它各 相的阻抗等效地降为较低的阻抗值。以此为出发点, 推导出解耦关系表达式,从而将复杂的三相 电压 的 控制,转化为单相 电压控制 问题 。并 以此解耦变换 为基础,通过分别对三相电压和零线相 电压进行独 立控制的方法,构造了高性能的四桥臂三相逆变器控制系统。
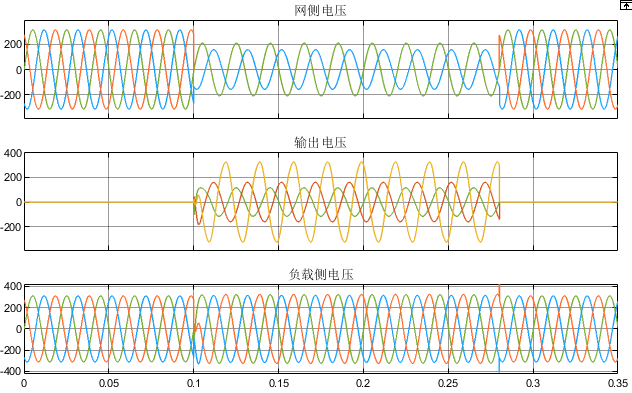
DVR系统由储能单元、逆变器和滤波电路构成DVR通过检测电源电压生成指令信号,对逆变器进行控制,叠加到负载电路中,从而保持敏感负载电压的稳定。
模型主体

仿真结果
参考文献
四桥臂三相逆变器的解耦控制——陈宏志
动态电压恢复器控制策略研究——蔡林海