Problem - C - Codeforces

目录

题意：

思路：

状态转移方程：

参考代码：

---

题意：

给两个长度为n数组a,b，和整数 l

任取若干下标，使得这个式子

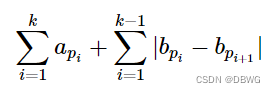不超过 l 的最多下标数。

思路：

可以根据右侧部分排好序依次减。

所以我们先对数组排序，按b的大小排。

然后用动态规划求 下标 i 之前 取 j 个 的最小值。

dp [ i ] [ j ]  =  dp [ k ] [ j -1 ]  + a[ i ] + b[ i ] - b[ k ]

k是指 i 之前的，取 j - 1个时的最小dp的下标。

但是这里有个k就三维了，不过我们可以这样优化：

 dp [ i ] [ j ]  =  dp [ k ] [ j -1 ] - b[ k ] + a[ i ] + b[ i ]

用 g[ j-1 ] = dp[ k ][j - 1] - b[ k ]

即 g[ j ] = dp[ k ][ j ] - b[ k ]

代表此前取 j 次最小的dp[ k ][ j ] - b[ k ]

我们在dp的过程中一直维护这个g[ j ]即可。

所以

状态转移方程：

dp [ i ] [ j ]  = g[ j ] + a[ i ] + b[ i ]

然后就可以去找数目最多的小于 l 的结果了。

参考代码：

注意dp时不能先次数再下标，因为本次可能为了更小，取了更靠后的数。。

#include<bits/stdc++.h>

using namespace std;

#define ll long long
#define endl "\n"
#define int long long
const ll inf = 1e9;
const ll MOD = 0x77777777737;
const int maxn = 1e9;
int dp[2003][2003];
void solve()
{
	int n, l;
	cin >> n >> l;
	vector<int>a(n), b(n),c(n),g(n+1);
	for (int i = 0; i < n; i++)
	{
		cin >> a[i] >> b[i];
	}
	iota(c.begin(), c.end(),0);
	sort(c.begin(), c.end(), [&](int l,int r)
		{
			return b[l] < b[r];
		});
	

	for (int i = 1; i <= n; i++)
		g[i] = LLONG_MAX;
	for (int i = 0; i < n; i++)
	{
		for (int j = i+1; j > 1; j--)//个数
		{
			//dp[i][j] = dp[k][j-1]-b[k]+a[c[i]]+b[c[i]];
			dp[i][j] = g[j-1]+a[c[i]]+b[c[i]];
			g[j] = min(dp[i][j] - b[c[i]],g[j]);
		}
		dp[i][1] = a[c[i]];
		g[1] = min(g[1],a[c[i]] -b[c[i]]);
	}



	//再用g去统计一下答案
	for (int i = 1; i <= n; i++)
		g[i] = LLONG_MAX;
	for (int i = 0; i < n; i++)
	{
		for (int j = i + 1; j >= 1; j--)//个数
		{
			g[j] = min(g[j], dp[i][j]);
		}
	}

	for (int i = n; i >= 0; i--)
	{
		if (g[i] <= l)
		{
			cout << i << endl;
			return;
		}
	}
}
signed main()
{
	ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
	int t = 1;
	cin >> t;
	while (t--)
	{
		solve();
	}
	return 0;
}