小顶堆和大顶堆
小顶堆(Min Heap)和大顶堆(Max Heap)是两种特殊的完全二叉树,它们遵循特定的堆属性,即父节点的值总是小于或等于(小顶堆)或者大于或等于(大顶堆)其子节点的值。这种结构使得堆的根节点包含了最大值或者最小值,这使得堆在很多算法中非常有用,尤其是在优先级队列的实现上。
小顶堆(Min Heap)
在小顶堆中,每个非叶子节点的值都必须大于或等于其子节点的值。这意味着堆的根节点包含了所有节点中的最小值。小顶堆通常用于那些需要快速访问最小元素的场景,比如实现优先队列也就是今天的力扣347题。
大顶堆(Max Heap)
在大顶堆中,每个非叶子节点的值都必须小于或等于其子节点的值。因此,堆的根节点包含了所有节点中的最大值。大顶堆通常用于需要快速访问最大元素的场景。
堆的操作
堆提供了几种基本操作:
insert(或add):向堆中添加一个新元素。remove:移除堆中的最大元素(在大顶堆中)或最小元素(在小顶堆中)。heapify:将一个数组转换成堆结构。extractMax/extractMin:从堆中提取并移除最大元素(在大顶堆中)或最小元素(在小顶堆中)。
在Java中实现堆,Java标准库中的PriorityQueue类就是基于堆实现的,默认情况下它使用小顶堆。可以指定一个Comparator来改变优先级队列的比较规则,从而可以实现大顶堆。
算法题
Leetcode 239. 滑动窗口最大值
题目链接:239. 滑动窗口最大值
大佬视频讲解:滑动窗口最大值视频讲解
个人思路
思路打结,不知道怎么实现
解法
单调队列
使用单调递减队列,将放进去窗口里的元素随着窗口的移动,队列也一进一出,每次移动之后,队列直接知道最大值是什么。
还有注意,队列没有必要维护窗口里的所有元素,只需要维护有可能成为窗口里最大值的元素,同时保证队列里的元素数值是由大到小的。
设计单调队列的时候,pop,和push操作要保持如下规则:
- poll(val):如果窗口移除的元素value等于单调队列的出口元素,那么队列弹出元素,否则不用任何操作
- add(val):如果add的元素value大于入口元素的数值,那么就将队列入口的元素弹出,直到add元素的数值小于等于队列入口元素的数值为止
保持如上规则,每次窗口移动的时候,只要deque.peek()就可以返回当前窗口的最大值。
class MyQueue {
Deque<Integer> deque = new LinkedList<>();
//弹出元素时,比较当前要弹出的数值是否等于队列出口的数值,如果相等则弹出;
void poll(int val) {
if (!deque.isEmpty() && val == deque.peek()) { //也要判断队列当前是否为空
deque.poll();
}
}
//添加元素时,如果要添加的元素大于入口处的元素,就将入口元素弹出,这样保证队列元素单调递减
//比如此时队列元素4,3,1 ;5将要入队,比4,3,1都大,所以都弹出,此时队列:5
void add(int val) {
while (!deque.isEmpty() && val > deque.getLast()) {
//push元素的数值小于等于队列入口元素的数值为止
deque.removeLast();
}
deque.add(val);
}
//队列队顶元素始终为最大值
int peek() {
return deque.peek();
}
}
class Solution {
public int[] maxSlidingWindow(int[] nums, int k) {
if (nums.length == 1) {
return nums;
}
int len = nums.length - k + 1;
int[] res = new int[len];//存放结果元素的数组
int num = 0;
MyQueue myQueue = new MyQueue();//自定义队列
//先将前k的元素放入队列
for (int i = 0; i < k; i++) {
myQueue.add(nums[i]);
}
res[num++] = myQueue.peek();
for (int i = k; i < nums.length; i++) {
myQueue.poll(nums[i - k]); //滑动窗口移除最前面的元素,移除是判断该元素是否放入队列
myQueue.add(nums[i]);//滑动窗口加入最后面的元素
res[num++] = myQueue.peek();//记录对应的最大值
}
return res;
}
}时间复杂度:O(n);(遍历数组)
空间复杂度:O(n);(辅助数组和队列)
Leetcode 347.前 K 个高频元素
题目链接:347.前 K 个高频元素
大佬视频讲解:前 K 个高频元素 视频讲解
个人思路
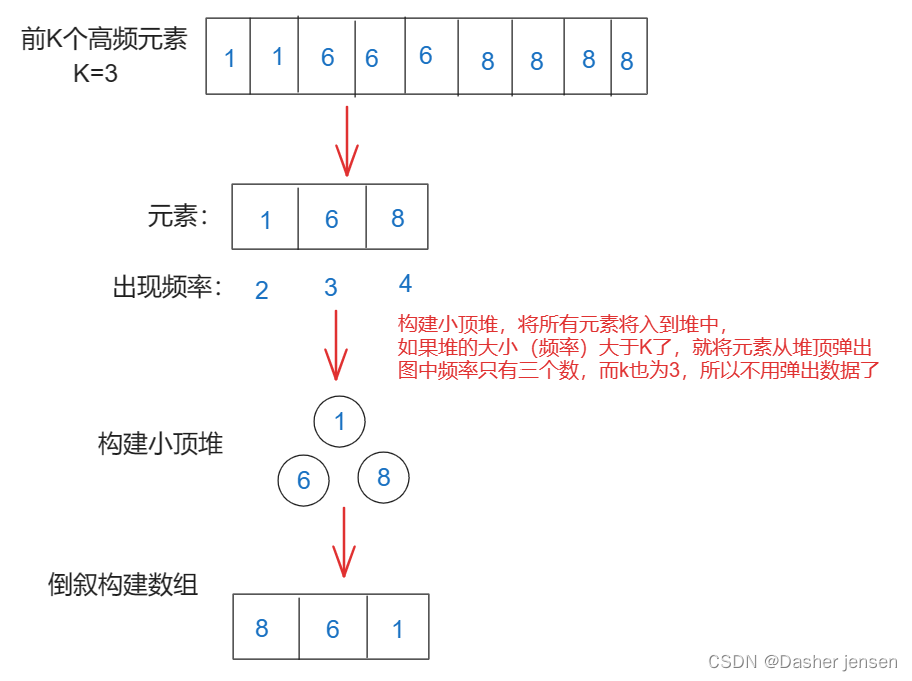
根据题意解答分为三步走,第一步要统计元素出现频率,第二步对频率排序,第三步找出前K个高频元素
解法
小顶堆
第一步统计元素出现的频率,这一类的问题可以使用map来进行统计。
第二步对频率进行排序,可以使用一种 容器适配器就是优先级队列,也就是一个披着队列外衣的堆,因为优先级队列对外接口只是从队头取元素,从队尾添加元素,再无其他取元素的方式,看起来就是一个队列。
第三步找出前k个高频元素,因为要统计最大前k个元素,只有小顶堆每次将最小的元素弹出,最后小顶堆里积累的才是前k个最大元素。
如下图所示
class Solution {
public int[] topKFrequent(int[] nums, int k) {
Map<Integer,Integer> map = new HashMap<>();//key为数组元素值,val为对应出现次数
for(int num:nums){
map.put(num,map.getOrDefault(num,0)+1);
}
//在优先队列中存储二元组(num,cnt),cnt表示元素值num在数组中的出现次数
//出现次数按从队头到队尾的顺序是从小到大排,出现次数最低的在队头(小顶堆)
PriorityQueue<int[]> pq = new PriorityQueue<>((pair1,pair2)->pair1[1]-pair2[1]);
for(Map.Entry<Integer,Integer> entry:map.entrySet()){//小顶堆只需要维持k个元素有序
if(pq.size()<k){//小顶堆元素个数小于k个时直接加
pq.add(new int[]{entry.getKey(),entry.getValue()});
}else{
if(entry.getValue()>pq.peek()[1]){//当前元素出现次数大于小顶堆的根结点
//弹出队头(小顶堆的根结点),即把堆里出现次数最少的那个删除,留下的就是出现次数多的了
pq.poll();
pq.add(new int[]{entry.getKey(),entry.getValue()});
}
}
}
int[] ans = new int[k];//结果数组
for(int i=k-1;i>=0;i--){//依次弹出小顶堆;先弹出的是堆的根,出现次数少,后面弹出的出现次数多
ans[i] = pq.poll()[0];
}
return ans;
}
}
时间复杂度:O(nlogk);(小顶堆构建)
空间复杂度:O(n);(优先队列,结果数组都不超过n)
以上是个人的思考反思与总结,若只想根据系列题刷,参考卡哥的网址代码随想录算法官网代码随想录算法官网代码随想录算法官网