一、一维数组前缀和

前缀和算法是一种用于处理数组的技术，它可以快速计算任何连续子数组的和。适合在多次查询中需要求解多个范围和的情况。使用前缀和算法可以将每次求和的时间复杂度从 O(n) 降低到 O(1)。

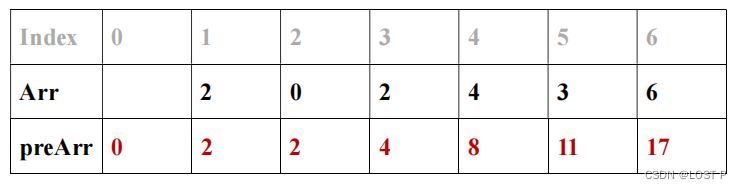
• 前缀和的思想是创建一个新数组 $Arr$，$preArr[i]$ 记录 $Arr[\mathrm{0...}i-1]$ 的累加和，如图：

• 那么，求索引区间 $[1,4]$ 内所有元素之和，可以通过 $preArr[5]-preArr[1]$ 得出。这样，便只需要做一次减法运算，避免了每次进行 for 循环调用，时间复杂度为常数 $O(1)$ 。

• 前缀和算法广泛用于处理数组求和问题，特别是当需要多次求解不同子数组的和时，它可以大大减少计算时间。

• 例如，班上有若干同学，每个同学有一个期末考试的成绩(满分100分)，那么请实现输入任意一个分数段，返回有多少同学的成绩在这个分数段内。

vector<int>scores; // 存储所有分数
vector<int>cnt(100 + 1, 0); //满分为100
for (auto& it : scores) // 记录每个分数有多少同学
{
	cnt[it]++;
}
for (int i = 1; i < scores.size(); i++) // 构造前缀和
{
	cnt[i] += cnt[i - 1];
}
// 利用前缀和数组进行差分查询

二、二维数组的前缀和

二维数组的前缀和是前缀和概念在二维空间的扩展。这个技巧通常用于处理二维数组上的区域和查询，特别适合于频繁查询数组特定子矩阵（子区域）内元素的总和的情况。

1.二维前缀和数组构建步骤：

1. 初始化 $preArr2$ 的所有元素为 0。

2. 遍历原始二维数组 $Arr2$，更新 $preArr2$ 中的值。对于 $preArr2$ 中的每个元素（位于 $(i,j)$），其值由以下元素决定：

   • 原数组 $Arr2$ 在 $(i-1,j-1)$ 的值（因为 $preArr2$ 比 $Arr2$ 多了一行和一列）。
   • $preArr2$ 中上方 $(i-1,j)$ 的前缀和。
   • $preArr2$ 中左侧 $(i,j-1)$ 的前缀和。
   • $preArr2$ 中左上角 $(i-1,j-1)$ 的前缀和，因为它被加了两次（在上方和左侧的和中），所以需要减去。

3. $preArr2[i][j]$ 的计算公式为：
   $$preArr2[i][j]=Arr2[i-1][j-1]+preArr2[i-1][j]+preArr2[i][j-1]-preArr2[i-1][j-1]$$

【注意】对于 $preArr2$ 的第一行和第一列，我们将它们保持为 0，这样可以简化边界条件的处理。

2.使用二维前缀和数组数组：

• 我们可以快速计算出原数组中任意子矩阵 $(x1,y1)$ 到 $(x2,y2)$ 的和，通过以下公式：
  $$sum=preArr2[x2+1][y2+1]-preArr2[x1][y2+1]-preArr2[x2+1][y1]+preArr2[x1][y1]$$
  这里 $(x1,y1)$ 是子矩阵左上角的坐标，$(x2,y2)$ 是子矩阵右下角的坐标。注意，因为 $preArr2$ 的定义，我们需要使用加一的索引来引用原始 $Arr2$ 中的相应区域。

3.举例

原始二维数组 Arr2:

1	2	3
4	5	6
7	8	9

二维前缀和数组 preArr2:

0	0	0	0
0	1	3	6
0	5	12	21
0	12	27	45

---

代码示例：

#include <iostream>
#include <vector>

using namespace std;

int main() {
    // 定义初始二维数组 Arr2
    vector<vector<int>> Arr2 = {{1, 2, 3}, {4, 5, 6}, {7, 8, 9}};

    // 获取数组的行数和列数
    int m = Arr2.size();
    int n = Arr2[0].size();

    // 构建二维前缀和数组 preArr2
    vector<vector<int>> preArr2(m + 1, vector<int>(n + 1, 0));
    for (int i = 1; i <= m; ++i) {
        for (int j = 1; j <= n; ++j) {
            preArr2[i][j] = Arr2[i - 1][j - 1] + preArr2[i - 1][j] + preArr2[i][j - 1] - preArr2[i - 1][j - 1];
        }
    }

    // 输出构建完成的二维前缀和数组
    for (int i = 0; i <= m; ++i) {
        for (int j = 0; j <= n; ++j) {
            cout << preArr2[i][j] << " ";
        }
        cout << "\n";
    }

    return 0;
}

本文部分内容参考自：【labuladong】前缀和/差分数组技巧精讲