山海自有归期
风雨自有相逢
CSDN 请求进入专栏
是否进入《数据结构专栏》?
确定
目录
三数之和
题目描述
输入输出样例
思路
代码测试
复杂度分析
三数之和
题目链接:三数之和
题目描述
给你一个整数数组
nums,判断是否存在三元组[nums[i], nums[j], nums[k]]满足i != j、i != k且j != k,同时还满足nums[i] + nums[j] + nums[k] == 0。请你返回所有和为
0且不重复的三元组。注意:答案中不可以包含重复的三元组。
输入输出样例
示例 1:
输入:nums = [-1,0,1,2,-1,-4] 输出:[[-1,-1,2],[-1,0,1]] 解释: nums[0] + nums[1] + nums[2] = (-1) + 0 + 1 = 0 。 nums[1] + nums[2] + nums[4] = 0 + 1 + (-1) = 0 。 nums[0] + nums[3] + nums[4] = (-1) + 2 + (-1) = 0 。 不同的三元组是 [-1,0,1] 和 [-1,-1,2] 。 注意,输出的顺序和三元组的顺序并不重要。示例 2:
输入:nums = [0,1,1] 输出:[] 解释:唯一可能的三元组和不为 0 。示例 3:
输入:nums = [0,0,0] 输出:[[0,0,0]] 解释:唯一可能的三元组和为 0 。提示:
3 <= nums.length <= 3000-10^5 <= nums[i] <= 10^5
思路
双指针+排序
<1>从 暴力 解法开始考虑问题
首先我们从(暴力枚举)的方法开始考虑
我们直接使用三重 for 循环枚举三元组,时间复杂度为 O(N^3) 这样效率是不高的,所以我们要在暴力的基础上不断的去 优化 算法
<2>利用 排序 算法整理去重数据
我们以示例一为例:nums = [-1,0,1,2,-1,-4]
那么[[0,1,-1],[-1,0,1]],[[1,2,-1]]是属于三元组的
注意:题目明确输出的顺序和三元组的顺序并不重要
所以我们在枚举完三元组后还需进行 去重 操作,为了避免后续数据整理上的麻烦
我们可以使用 排序 算法让数组有序化,这样 相同 的三元组仅仅只有一种排列形式
[[0,1,-1],[-1,0,1]] 的去重问题就好解决了
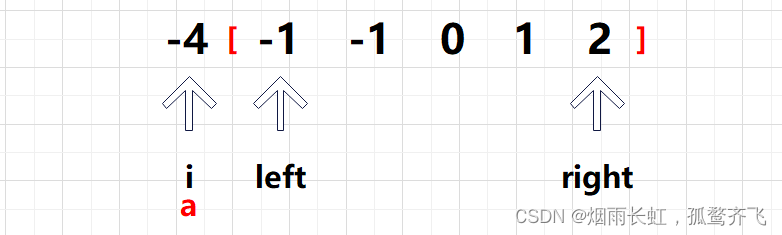
<3>利用 双指针 优化 暴力 解法

(1) 固定一个数a (2) 在 a 的后面区间利用 双指针 算法,快速找到 两数之和 等于 -a 即
nums[left]+nums[right] = -a
<4>细节问题的处理
(1)去重问题
因为我们已经排好序了,对于重复的元素我们可以直接控制下标移动
采用 set容器 去重 虽然便捷,但是在面试中并不建议 利用单调性去重 <1>找到一种结果之后,left 和 right 指针要跳过重复元素
<2>当使用完一次双指针算法之后,i 也需要跳过重复元素我们以下的代码测试采用单调性的性质去重
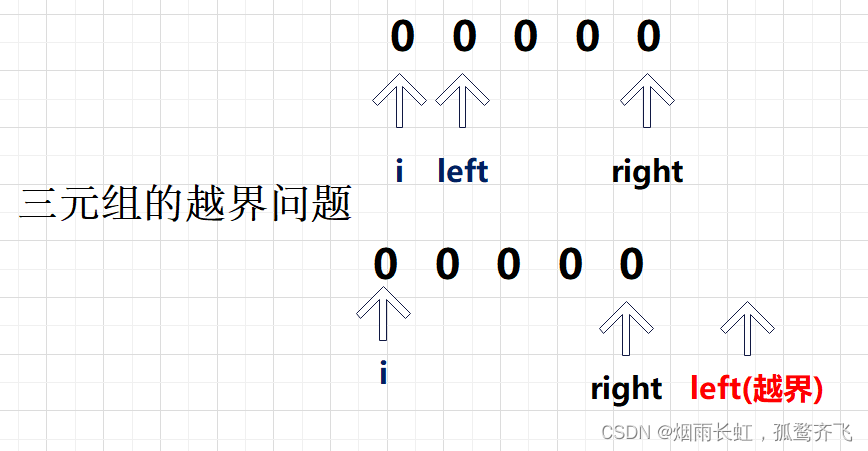
(2)边界问题
我们要设置数组边界,防止数组越界
(3)数据遗漏
找到一种结果之后,不要 停 ,继续缩小区间,继续寻找
(4)细节上的优化
利用三元组 nums[left]+nums[right] = -a 的性质优化代码
代码测试
class Solution { public: vector<vector<int>> threeSum(vector<int>& nums) { //创建容器存储三元组 vector<vector<int>> ret; //排序 sort(nums.begin(),nums.end()); int n = nums.size(); for(int i = 0;i<n;) { //细节优化 if(nums[i]>0) break; int left = i+1,right = n-1; int m = - nums[i]; while(left<right) { int sum = nums[left]+nums[right]; if(sum>m) right--; else if(sum<m) left++; else if(sum == m) { //找到三元组,并装进ret中 ret.push_back({nums[i],nums[left],nums[right]}); left++; right--; //去重,双指针边界考虑 while(left<right && nums[left] == nums[left-1]) left++; while(left<right && nums[right] == nums[right+1]) right--; } } //去重,i 边界考虑 i++; while(i<n && nums[i] == nums[i-1]) i++; } return ret; } };
复杂度分析
时间复杂度:O(N)
空间复杂度:O(logN)