1 K-Medoid算法
K-Medoid(也称为围绕Medoid的划分)算法是由Kaufman和Rousseeuw于1987年提出的。中间点可以定义为簇中的点,其与簇中所有其他点的相似度最小。
K-medoids聚类是一种无监督的聚类算法,它对未标记数据中的对象进行聚类。
在本文中,我们将了解什么是K-medoids聚类?为什么我们需要它?首先,得出第二个问题的答案:我们需要它,因为K-means聚类有一些缺点,即在这方面,具有极大值的对象可能会严重扭曲对象在簇/组中的分布。因此,它对异常值很敏感。它通过K-medoids聚类(也称为K-means聚类的临时版本)来解决。
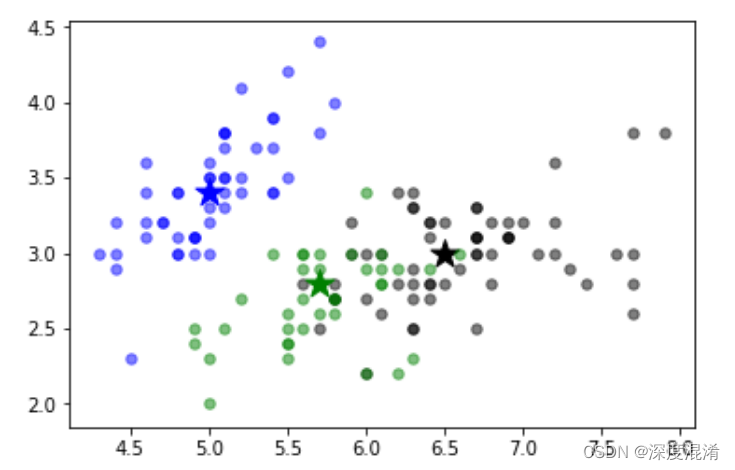
在K-medoids聚类中,我们将medoid作为参考点,而不是像K-means聚类那样将簇中对象的质心作为参考点。中间体是群集中位置最集中的对象,或其与所有对象的平均相异性最小。因此,K-medoids算法比K-means算法对噪声更具鲁棒性。

2 K-medoids聚类有三种算法:
PAM(围绕medoid分区)
CLARA(群集大型应用程序)
CLARANS(“随机化”克拉拉)。
在这些PAM中,PAM被认为是最强大的,并被广泛使用。然而,PAM有一个缺点,因为它的时间复杂性(我们将在后面讨论)。因此,在本文中,我们将详细了解PAM算法。
算法
现在我们来看看k-medoids算法内部的情况,如下所示:
步骤1:在给定的数据空间D中初始化k个集群。
步骤2:从数据中的n个对象中随机选择k个对象,并将k个对象分配给k个簇,这样每个对象都被分配给一个且仅一个簇。因此,它成为每个集群的初始中间层。
步骤3:对于所有剩余的非medoid对象,计算所有medoid的成本(通过欧几里德、曼哈顿或切比雪夫方法计算的距离)。
步骤4:现在,将每个剩余的非中间层对象指定给该簇,该簇的中间层到该对象的距离与其他簇的中间层相比是最小的。
步骤5:计算总成本,即,它是所有非medoid对象与其群集medoid之间距离的总和,并将其分配给dj。
第六步:随机选择一个非中间体对象i。
步骤7:现在,暂时将对象i与medoid j交换,然后重复步骤5以重新计算总成本并将其分配给di。
步骤8:如果di<dj,则将步骤7中的临时交换永久化,以形成新的k medoid集。否则撤消步骤7中完成的临时交换。
步骤9:重复步骤4、步骤5、步骤6、步骤7、步骤8。直到没有变化;
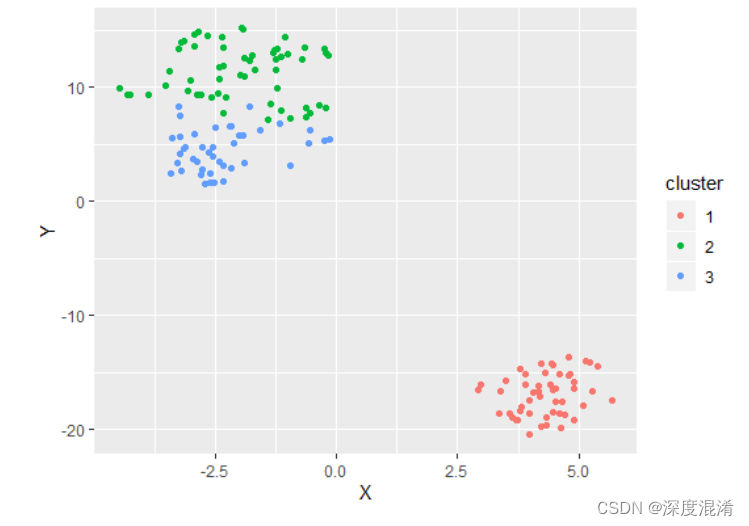
3 PAM、CLARA、CLARANS之间的差异
3.1 PAM
与k-means算法相比,它有效地处理了数据中存在的噪声和异常值;因为它使用medoid将对象划分为簇,而不是k-means中的质心。
因为它对整体数据执行聚类,而不是仅对数据集中选定的样本执行聚类。因此,对于大型数据集,它不能有效地工作。
PAM的计算成本很高,因为它在整个数据集上执行集群。
其每次迭代的时间复杂度为O(k*(n-k)^2);其中n是数据中对象的数量,k是簇的数量。
3.2 CLARA
在CLARA中,它首先从数据集中选择数据样本,对这些样本应用PAM,然后从这些样本中输出最佳聚类。
因为它通过从数据中选择样本来应用聚类,所以它处理的是较大的数据集。
随着样本量的增加,其有效性也会增加,反之亦然。
假设它绘制了多个较小的样本,并在其上进行了良好的聚类。如果所选样本有偏差,则不能很好地对总体数据进行聚类。
3.3 CLARANS
在每一步中,它都会选择一个邻居样本进行检查。因此,它不会将搜索限制在特定区域。它给出了基于总体数据的结果。
现在,因为它在每一步都会检查邻居。因此,当集群和对象数量很大时,这很耗时。
在CLARANS中,有一个参数表示局部最优值的数量。就像找到了局部最优值一样,它再次开始随机选取一个节点来找到新的局部最优值。要限制此过程,请在启动时指定上述参数。
因为,它的时间复杂度是O(n^2)。因此,它是其他k-medoids算法中最有效的算法;返回更高质量的群集。
3.4 K-medoids算法的优点
与其他分割算法相比,它有效地处理了数据中存在的噪声和异常值;因为它使用medoid将对象划分为集群。
易于实现且易于理解。
与其他分割算法相比,K-Medoid算法速度相对较快。
它以固定的迭代次数输出最终的对象簇。
3.5 K-medoids算法的缺点
对于同一数据集上的不同运行,可能会产生不同的聚类,因为最初,我们从所有数据对象中随机选择k个medoid,并将它们逐个分配给每个聚类,使其成为该聚类的初始medoid。
它在开始时固定了k(簇/组的数量)的值,因此我们不知道k的值是多少,结果是准确和可区分的。
它的总体计算时间和对象在簇或组中的最终分布取决于初始划分。
因为在这里,我们根据对象与质心的最小距离(而不是k-means中的质心)将对象分布在簇中。因此,在任意形状的聚类中对数据进行聚类是没有用的。
源程序
using System;
using System.IO;
using System.Text;
using System.Linq;
using System.Collections.Generic;
namespace Legalsoft.Truffer.Algorithm
{
public class K_Medoids
{
public static List<Crows> Pam(List<Indivaduls> indivadulses, List<Indivaduls> centerPoints)
{
List<Crows> firstCrows = K_medoids(indivadulses, centerPoints);
List<Indivaduls> resultCenterPoints = new List<Indivaduls>();
for (int i = 0; i < firstCrows.Count; i++)
{
resultCenterPoints.Add(firstCrows[i].CenterPoint);
List<Crows> oldOtherCrows = new List<Crows>();
oldOtherCrows.AddRange(firstCrows);
oldOtherCrows.RemoveAt(i);
double oldDiff = AbsoluteDiff(firstCrows[i], oldOtherCrows);
int count = firstCrows[i].CrowsPoint.Count;
for (int j = 0; j < count; j++)
{
List<Indivaduls> newCenterPoints = new List<Indivaduls>();
newCenterPoints.AddRange(centerPoints);
newCenterPoints.RemoveAt(i);
newCenterPoints.Add(firstCrows[i].CrowsPoint[j]);
List<Indivaduls> newOtherCrowsCenterPoints = new List<Indivaduls>();
newOtherCrowsCenterPoints.AddRange(centerPoints);
newOtherCrowsCenterPoints.RemoveAt(i);
List<Crows> newCrows = K_medoids(indivadulses, newCenterPoints);
List<Crows> newOtherCrows = new List<Crows>();
Crows newCrow = new Crows();
foreach (Crows crow in newCrows)
{
if (newOtherCrowsCenterPoints.MyContains(crow.CenterPoint))
{
newOtherCrows.Add(crow);
}
else
{
newCrow = crow;
}
}
double newDiff = AbsoluteDiff(newCrow, newOtherCrows);
if (newDiff < oldDiff)
{
resultCenterPoints[i] = newCrow.CenterPoint;
oldDiff = newDiff;
}
}
}
List<Crows> resultCrows = K_medoids(indivadulses, resultCenterPoints);
return resultCrows;
}
public static List<Crows> K_medoids(List<Indivaduls> indivadulses, List<Indivaduls> centerPoints)
{
List<Crows> resultCrows = new List<Crows>();
int indivadulsCount = indivadulses.Count;
for (var i = 0; i < centerPoints.Count; i++)
{
resultCrows.Add(new Crows() { CenterPoint = centerPoints[i] });
}
for (int i = 0; i < indivadulsCount; i++)
{
if (!centerPoints.MyContains(indivadulses[i]))
{
int myNumber = 0;
double firstDic = P2PDistance(indivadulses[i], resultCrows[0].CenterPoint);//该点与第一个中心的距离
for (int j = 1; j < resultCrows.Count; j++)
{
double otherDic = P2PDistance(indivadulses[i], resultCrows[j].CenterPoint);
if (otherDic < firstDic)
{
firstDic = otherDic;
myNumber = j;
}
}
resultCrows[myNumber].CrowsPoint.Add(indivadulses[i]);
}
}
return resultCrows;
}
public static double AbsoluteDiff(Crows centerCrow, List<Crows> otherPoints)
{
int countCrows = otherPoints.Count;
double distance = Distance(centerCrow);
for (var i = 0; i < countCrows; i++)
{
distance += Distance(otherPoints[i]);
}
return distance;
}
public static double Distance(Crows crow)
{
int pointCount = crow.CrowsPoint.Count;
double distance = 0.0;
for (var i = 0; i < pointCount; i++)
{
distance += P2PDistance(crow.CenterPoint, crow.CrowsPoint[i]);
}
return distance;
}
public static double P2PDistance(Indivaduls p1, Indivaduls p2)
{
if (p1.Numbers.Count != p2.Numbers.Count || p1.Numbers.Count == 0)
{
throw new Exception();
}
int dimension = p1.Numbers.Count;
double result = 0.0;
for (int i = 0; i < dimension; i++)
{
result += (p1.Numbers[i] - p2.Numbers[i]) * (p1.Numbers[i] - p2.Numbers[i]);
}
return Math.Sqrt(result);
}
}
public class Indivaduls
{
public List<double> Numbers { get; set; } = new List<double>();
public Indivaduls()
{
}
public bool MyEquals(Indivaduls obj)
{
if (obj.Numbers.Count != Numbers.Count)
{
return false;
}
for (int i = 0; i < Numbers.Count; i++)
{
if (Numbers[i] != obj.Numbers[i])
{
return false;
}
}
return true;
}
}
public class Crows
{
public List<Indivaduls> CrowsPoint { get; set; } = new List<Indivaduls>();
public Indivaduls CenterPoint { get; set; } = new Indivaduls();
public Crows()
{
}
}
public static class ExpandList
{
public static bool MyContains(this List<Indivaduls> indivadulses, Indivaduls point)
{
foreach (var indivadulse in indivadulses)
{
if (point.MyEquals(indivadulse))
{
return true;
}
}
return false;
}
}
}